Maximum dan Minimum

Dalam analisis matematis, maksimum dan minimum suatu fungsi mengacu pada nilai terbesar dan terkecil yang dapat diambil oleh fungsi tersebut. Nilai-nilai ini, yang biasa disebut sebagai nilai ekstrem, dapat didefinisikan dalam dua konteks: pertama, dalam rentang tertentu, yang dikenal sebagai nilai ekstrem lokal atau relatif, dan kedua, dalam seluruh rentang fungsi, yang dikenal sebagai nilai ekstrem global atau absolut. Konsep ini diperkenalkan dan dikembangkan oleh ahli matematika awal, dengan Pierre deFermat menjadi salah satu orang pertama yang mengusulkan teknik umum dan cukup untuk mencari nilai maksimum dan minimum dalam konteks fungsi matematika.

Dalam teori himpunan, maksimum dan minimum suatu himpunan mengacu pada elemen terbesar dan terkecil dari himpunan tersebut. Perlu diperhatikan bahwa himpunan tak hingga, seperti himpunan bilangan real, tidak memiliki nilai minimum dan maksimum karena tidak ada elemen yang membatasi nilai terbesar atau terkecil.Dalam statistika, terdapat konsep terkait yang disebut maksimum dan minimum sampling, yang mengacu pada nilai terbesar dan terkecil dalam suatu sampel data. Sebagai bagian integral dari analisis statistik, pemahaman maksimum dan minimum sangat penting untuk menilai distribusi data dan tren umum dalam suatu populasi.

Mencari Nilai Minimum dan Maximum

Menemukan maxima dan minima global adalah tujuan optimasi matematis. Jika suatu fungsi kontinu dalam interval tertutup, maka menurut teorema nilai ekstrim terdapat maksimum global dan minimum global. Selain itu, maksimum (atau minimum) global harus merupakan maksimum (atau minimum) lokal dalam domain atau pada batas domain. Jadi metode mencari maksimum (atau minimum) global adalah dengan mengamati semua maksimum (atau minimum) lokal di dalamnya sertamaksimum (atau minimum) dari titik-titik pada batas dan menemukan yang terbesar (atau lebih kecil).

Untuk fungsi terdiferensiasi, teorema Fermat menyatakan bahwa ekstrem lokal dalam suatu wilayah harus terjadi pada titik kritis (atau titik yang turunannya sama dengan nol). Namun, tidak semua titik balik bersifat ekstrem. Kita sering kali dapat membedakan apakah suatu titik kritis merupakan maksimum lokal, minimum lokal, atau bukan keduanya dengan menggunakan uji turunan pertama, uji turunan kedua, atau uji turunan orde tinggi, dengan memperhatikan diferensiasi yang cukup.

Untuk setiap fungsi yang ditentukan oleh bagian-bagian, nilai maksimum (atau minimum) dapat ditemukan dengan mencari nilai maksimum (atau minimum) dari masing-masing bagian secara terpisah dan kemudian menentukan mana yang terbesar (atau terkecil).

Fungsi Lebih dari satu Variabel

Kondisi serupa berlaku untuk fungsi dengan lebih dari satu variabel. Misalnya, pada gambar (yang dapat diperbesar) di sebelah kanan, kondisi yang diperlukan untuk maksimum lokal serupa dengan kondisi untuk fungsi variabel tunggal. Turunan parsial pertama dari z (variabel yang akan dimaksimalkan) adalah nol pada maksimumnya (titik terang di bagian atas gambar). Turunan parsial kedua bernilai negatif. Ini hanyalah kondisi yang diperlukan, namun tidak cukup untuk mencapai maksimum lokal sebesarkarena mungkin terdapat titik pelana.Agar kondisi ini dapat diselesaikan secara optimal, fungsi z juga harus terdiferensiasi sempurna. Uji turunan parsial kedua dapat membantu mengklasifikasikan titik tersebut sebagai maksimum relatif atau minimum relatif. Sebaliknya, terdapat perbedaan yang signifikan antara peran satu variabel dan peran beberapa variabel dalam mengidentifikasi kondisi ekstrem global. Misalnya, jika fungsi terdiferensiasi hingga f yang didefinisikan pada interval tertutup pada garis nyata mempunyai titik kritisyang merupakan minimum lokal, maka fungsi tersebut juga merupakan minimum global (gunakan teorema nilai antara dan teorema Rolle untuk membuktikannya) . dengan kontradiksi). Dalam dua dimensi atau lebih argumen ini gagal.Hal ini tercermin dari fungsinya.

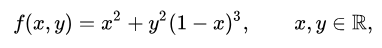
yang titik kritisnya hanya di (0,0), yang merupakan minimum lokal dengan f (0,0) = 0. Namun, tidak bisa menjadi minimum global, karena f (2,3) = −5.

Maxima atau minima dari suatu fungsi

Jika jangkauan suatu fungsi yang ekstremnya dicari terdiri dari fungsi itu sendiri (yaitu jika ekstrem suatu fungsi dapat ditemukan), maka ekstremnya ditemukan dengan kalkulus variasi.

Sehubungan dengan himpunan

Paragraf tersebut menjelaskan konsep maxima dan minima dalam konteks himpunan terurut. Jika suatu himpunan terurut S mempunyai m anggota terbesar, maka m disebut anggota maksimum himpunan tersebut, ditulis maks(S). Jika S adalah himpunan bagian dari himpunan terurut T dan m adalah elemen terbesar dari S dengan keteraturan karena T, maka m adalah batas atas terkecil dari S dalam T. Konsep serupa berlaku untuk elemen terkecil, elemen minimal, dan elemen terkecil. elemen bawah terbesar. melompat.

Fungsi maksimum dan minimum untuk himpunan digunakan dalam database dan dapat dihitung dengan cepat menggunakan partisi.Dalam pengurutan parsial umum, elemen terkecil dan elemen minimal tidak boleh tertukar. Dalam himpunan terurut sebagian (poset), elemen terbesar adalah batas atas himpunan, sedangkan elemen maksimum m dari sebuah poset A memenuhi m ≤ b untuk setiap b di A, dan jika m ≤ b maka m = b. Elemen terkecil atau terbesar dari sebuah poset adalah unik, tetapi sebuah poset dapat memiliki beberapa elemen minimum atau maksimum.

Dalam himpunan terurut lengkap, himpunan tersebut dapat mempunyai paling banyak satu elemen minimum dan satu elemen maksimum. Pada himpunan terurut sempurna, elemen minimum adalah elemen terkecil dan elemen maksimum adalah elemen terbesar.Jika rantainya berhingga, maka selalu mempunyai maksimum dan minimum. Jika rantainya tidak terbatas, maka tidak harus memiliki maksimum atau minimum. Misalnya himpunan bilangan asli tidak mempunyai nilai maksimum, namun mempunyai nilai minimum. Jika suatu rantai tak terhingga S dibatasi, penutupan Cl(S) dari himpunan tersebut dapat mempunyai minimum dan maksimum, yang disebut batas bawah terbesar dan batas atas terkecil dari S.

Disadur dari: en.wikipedia.org

Sistem nonlinier

Sistem nonlinier dalam matematika dan sains adalah sistem yang perubahan keluarannya tidak sebanding dengan perubahan masukan. Masalah nonlinier menarik perhatian para insinyur, ahli biologi, fisikawan, matematikawan, dan ilmuwan lain karena sebagian besar sistem pada dasarnya bersifat nonlinier. Sistem nonlinier dalam matematika dapat dijelaskan dengan sistem persamaan nonlinier, yaitu kumpulan persamaan simultan yang variabel-variabelnya tidak diketahui muncul sebagai variabel polinomial berderajatlebih besar dari satu atau sebagai argumen fungsi yang bukan polinomial berderajat satu. Karena persamaan dalam sistem nonlinier tidak dapat ditulis sebagai kombinasi linier dari variabel atau fungsi yang tidak diketahui yang muncul di dalamnya, sistem tersebut dapat dianggap nonlinier meskipun fungsi linier yang diketahui muncul dalam persamaan tersebut.

Secara umum, suatu persamaan diferensial dianggap linier jika persamaan tersebut linier terhadap fungsi yang tidak diketahui dan turunannya, meskipun persamaan tersebut mungkin nonlinier terhadapvariabel lain yang muncul di dalamnya.Karena persamaan diferensial dinamis nonlinier sulit diselesaikan, sistem nonlinier biasanya didekati dengan persamaan linier (linierisasi). Ini bekerja dengan baik hingga tingkat presisi dan rentang nilai masukan tertentu, tetapi beberapa fenomena menarik seperti soliton, chaos, dan singularitas disembunyikan oleh linearisasi. Oleh karena itu, beberapa aspek perilaku dinamis sistem nonlinier mungkin tampak berlawanan dengan intuisi, tidak dapat diprediksi, atau bahkan kacau. Meskipun perilaku kacaumungkin menyerupai perilaku acak, sebenarnya perilaku tersebut tidak acak. Misalnya, beberapa aspek iklim tampak kacau, dengan perubahan sederhana pada satu bagian sistem mempunyai dampak kompleks pada keseluruhan sistem.Ketidaklinieran ini adalah salah satu alasan mengapa perkiraan jangka panjang yang akurat tidak mungkin dilakukan dengan teknologi saat ini.

Persamaan aljabar nonlinier

Persamaan aljabar nonlinier, disebut juga persamaan polinomial, didefinisikan dengan menyamakan polinomial (yang derajatnya lebih besar dari satu) menjadi nol. Sebagai contoh,

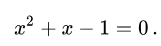
Algoritme pencarian akar dapat digunakan untuk mencari solusi unik persamaan polinomial (yaitu himpunan nilai variabel yang memenuhi persamaan tersebut). Namun, sistem persamaan aljabar lebih kompleks; Studinya menjadi motivasi untuk bidang geometri aljabar, cabang matematika modern yang sulit. Sulit juga menentukan apakah sistem aljabar mempunyai solusi kompleks (lihat teorema nol Hilbert). Namun, untuk sistem dengan jumlah solusi kompleks yang terbatas,sistem persamaan polinomial ini sekarang telah dipahami dengan baik dan terdapat metode yang efisien untuk menyelesaikannya.

Hubungan perulangan nonlinier

Relasi perulangan nonlinier mendefinisikan barisan suku-suku dalam suatu barisan sebagai fungsi nonlinier dari suku-suku sebelumnya. Contoh hubungan perulangan nonlinier mencakup peta logistik dan hubungan yang menentukan berbagai rangkaian Hofstadter. Model nonlinier diskrit, yang mewakili kelas luas hubungan perulangan nonlinier, mencakup model NARMAX (Nonlinear Autoregressive Moving Average dengan Input Eksogen) dan metode terkait untuk mengidentifikasi dan menganalisis sistem nonlinier.Pendekatan ini dapat digunakan untuk mempelajari berbagai perilaku nonlinier kompleks dalam domain waktu, frekuensi, dan spatiotemporal.

Persamaan diferensial nonlinier

Suatu sistem persamaan diferensial tergolong nonlinier jika bukan merupakan sistem persamaan linier. Masalah persamaan diferensial nonlinier sangat beragam dan cara penyelesaiannya bergantung pada sifat masalahnya. Persamaan Navier-Stokes dalam dinamika fluida dan persamaan Lotka-Volterra dalam biologi merupakan contoh persamaan diferensial nonlinier. Tantangan terbesar dalam permasalahan nonlinier adalah sulitnya menggabungkan solusi yang sudah diketahui menjadi solusi baru karena tidak adanya prinsip superposisi seperti pada permasalahan linier. Meskipun beberapa solusi khusus dapat ditemukan untuk persamaan nonlinier, prinsip superposisi yang buruk menyulitkan pembuatan solusi baru.

Persamaan diferensial parsial

Saat mempelajari persamaan diferensial parsial nonlinier, pendekatan dasar yang paling umum adalah mengubah variabel (atau soal) sehingga soal yang dihasilkan lebih sederhana, mungkin linier. Terkadang persamaan tersebut dapat diubah menjadi satu atau lebih persamaan diferensial biasa, seperti dalam metode pemisahan variabel, yang selalu berguna terlepas dari apakah persamaan diferensial biasa yang dihasilkan mempunyai solusi atau tidak.Taktik lain yang umum, meskipun kurang matematis, yang sering digunakan dalam mekanika termal dan fluida adalah melakukan analisis penskalaan untuk menyederhanakan persamaan natural umum dalam masalah nilai batas tertentu.

Misalnya, dalam kasus aliran satu dimensi, laminar, transien dalam pipa melingkar, persamaan Navier-Stokes yang sangat nonlinier dapat disederhanakan menjadi persamaan diferensial parsial linier; Analisis penskalaan memberikan kondisi di mana aliran bersifat laminar dan satu dimensi serta menghasilkan persamaan yang disederhanakan.Metode lainnya adalah mempelajari sifat-sifat dan menerapkan metode persamaan diferensial biasa yang dijelaskan di atas.

Disadur dari : en.wikipedia.org

Riset Operasi

Riset Operasi (OR), disingkat Riset Operasi atau Ilmu Manajemen, adalah disiplin ilmu yang berhubungan dengan pengembangan dan penerapan metode analisis untuk meningkatkan pengambilan keputusan. Teknik dari ilmu matematika lain seperti pemodelan, statistika dan optimasi digunakan dalam riset operasi untuk memperoleh solusi optimal atau mendekati optimal ketika menyelesaikan masalah pengambilan keputusan. Karena fokusnya pada aplikasi praktis, Riset Operasibersinggungan dengan banyak disiplin ilmu lain, termasuk teknik industri. Biasanya, riset operasi bertujuan untuk menentukan nilai ekstrim dari suatu tujuan dunia nyata, apakah itu nilai maksimum (manfaat, efisiensi, atau hasil) atau minimum (kerugian, risiko, atau biaya). Teknik-teknik ini berasal dari upaya militer sebelum Perang Dunia II dan telah dikembangkan lebih lanjut untuk memecahkan berbagai masalah di berbagai industri.

Gambaran Umum

Riset Operasi (OR) melibatkan pengembangan dan penggunaan berbagai teknik dan metode pemecahan masalah untuk meningkatkan pengambilan keputusan dan efisiensi, seperti: B. Simulasi, optimasi matematis, teori antrian, model proses stokastik, proses pengambilan keputusan, keputusan Markov, metode ekonometrik, data. Analisis amplop, pendekatan prioritas ordinal, jaringan saraf, sistem pakar, analisis keputusan dan metode analisis hierarki.

Hampir semua teknik ini melibatkan pembuatan model matematika untuk menggambarkan sistem. Karena sebagian besar bidang ini bersifat komputasi dan statistik, Internet of Things juga terkait erat dengan ilmu komputer dan analitik. Atau, peneliti yang menghadapi masalah baru perlu mengidentifikasi teknik yang paling sesuai dengan jenis sistem, tujuan perbaikan, dan batasan waktu serta daya komputasi, atau mengembangkan teknik baru yang khusus untuk masalah tersebut. Sub-disiplin utama riset operasi modern yang diidentifikasi oleh jurnal Operations Research meliputi:

1. Teknologi komputer dan informasi
2. Rekayasa keuangan
3. Manufaktur, ilmu jasa dan manajemen rantai pasokan
4. Pemodelan kebijakan dan kerja di sektor publik
5. Manajemen Pendapatan
6. Simulasi
7. Model stokastik
8. Teori Lalu Lintas (Matematika)
9. Teori permainan untuk strategi.
10. Pemrograman linier
11. Pemrograman nonlinier
12. Pemrograman integer dikhususkan untuk permasalahan NP-complete.
13. Pemrograman dinamis di bidang teknik dirgantara dan ekonomi.
14. Teori informasi untuk digunakan dalam kriptografi, komputasi kuantum.
15. Pemrograman kuadrat untuk menyelesaikan persamaan dan fungsi kuadrat.

Sejarah

Dalam beberapa dekade setelah dua perang dunia, alat penelitian operasional semakin banyak digunakan untuk memecahkan permasalahan dalam bisnis, industri, dan masyarakat. Sejak saat itu, riset operasi telah menjadi bidang yang banyak digunakan di berbagai industri, mulai dari petrokimia, maskapai penerbangan, hingga keuangan, logistik, dan pemerintahan. Fokusnya adalah pada pengembangan model matematika yang dapat digunakan untuk menganalisis dan mengoptimalkan sistem yang sebagian kompleks dan telah menjadi area aktif penelitian akademis dan industri.

Asal usul sejarah

Pada abad ke-17, matematikawan Blaise Pascal dan Christiaan Huygens memecahkan masalah yang terkadang melibatkan keputusan rumit dengan menggunakan ide teori permainan dan nilai yang diharapkan. Matematikawan lain seperti Pierre de Fermat dan Jacob Bernoulli memecahkan masalah jenis ini dengan menggunakan pemikiran kombinatorial.Investigasi Charles Babbage terhadap biaya transportasi dan penyortiran surat mengarah pada penciptaan "pos penny" universal di Inggris pada tahun 1840, serta studi tentang perilaku dinamis kendaraan kereta api dalam mempertahankan ukuran GWR. Pada awal abad ke-20, studi tentang manajemen inventaris dapat dianggap sebagai asal mula riset operasi modern, dan Ford W. Harris mengembangkan ekonomi kuantitas pesanan pada tahun 1913. Riset operasi mungkin berawal dari upaya perencana militer selama Perang Dunia. Saya suka teori konvoi dan hukum Lanchester.

Percy Bridgman memperkenalkan riset operasi untuk masalah fisik pada tahun 1920an dan kemudian mencoba memperluasnya ke ilmu-ilmu sosial.Penelitian operasional modern dimulai pada tahun 1937 di stasiun penelitian Bawdsey di Inggris atas prakarsa manajer stasiun A. P. Rowe dan Robert Watson-Watt. Rowe mengembangkan ide ini untuk menganalisis dan meningkatkan sistem radar peringatan dini Inggris yang disebut “Chain Home” (CH). Rowe pertama-tama menganalisis pengoperasian radar dan jaringan komunikasinya, lalu berfokus pada perilaku personel operasional.Hal ini akan mengungkap keterbatasan jaringan CH yang tidak disadari dan memungkinkan dilakukannya tindakan perbaikan. Para ilmuwan di Inggris (termasuk Patrick Blackett, Cecil Gordon, Solly Zuckerman, C. H. Waddington, Owen Wansbrough-Jones, Frank Yates, Jacob Bronowski, dan Freeman Dyson) dan Amerika Serikat (George Dantzig) mencari cara untuk membuat keputusan logistik dan perencanaan yang lebih baik. Pendidikan.

Masalah yang ditangani

Riset operasi menangani berbagai masalah seperti analisis jalur kritis atau perencanaan proyek, perancangan tata letak peralatan di pabrik atau komponen dalam chip komputer untuk mengurangi waktu produksi, optimalisasi jaringan seperti penyiapan jaringan telekomunikasi atau sistem tenaga untuk menjaga kualitas layanan saat terjadi gangguan. . serta masalah alokasi sumber daya, energi, lokasi fasilitas dan pembagian tugas. Selain itu, riset operasi digunakan dalam manajemen rantai pasokan, produksiproyek, taktik respons pelanggan, otomatisasi operasi manusia, globalisasi operasi untuk memanfaatkan material, mengurangi tenaga kerja dan lahan yang lebih murah, mengelola transportasi dan pengiriman barang, serta dalam menentukan kondisi optimal. Penetapan harga dalam berbagai konteks ritel dan B2B. Disiplin ini juga banyak digunakan di pemerintahan untuk kebijakan berbasis bukti.

Manajemen Sains

Pada tahun 1967, Stafford Beer menggambarkan bidang ilmu manajemen sebagai “penggunaan bisnis dari riset operasi.” Seperti riset operasi itu sendiri, ilmu manajemen (MS) adalah cabang matematika terapan interdisipliner yang didedikasikan untuk perencanaan keputusan yang optimal dan memiliki hubungan yang kuat dengan ilmu ekonomi, administrasi bisnis, teknik, dan ilmu lainnya. MS menggunakan berbagai prinsip, strategi, dan metode analisis berdasarkan penelitian ilmiah, termasuk model matematika, statistik, dan algoritme numerik
untuk meningkatkan kemampuan organisasi dalam membuat keputusan manajemen yang rasional dan masuk akal dengan memberikan solusi optimal atau mendekati optimal untuk masalah yang terkadang rumit. masalah yang dicapai. masalah pengambilan keputusan yang kompleks. Ilmuwan manajemen membantu perusahaan mencapai tujuan mereka menggunakan metode ilmiah riset operasi.

Misi ilmuwan manajemen adalah menggunakan teknik berbasis sains yang rasional dan sistematis untuk memberikan informasi dan meningkatkan berbagai jenis keputusan.Tentu saja, teknik manajemen ilmiah tidak terbatas pada penerapan bisnis tetapi dapat diterapkan pada militer, kedokteran, administrasi publik, badan amal, kelompok politik, atau kelompok masyarakat.

Ilmu manajemen berkaitan dengan pengembangan dan penerapan model dan konsep yang dapat membantu mengungkap permasalahan manajemen dan menyelesaikan permasalahan manajemen, serta merancang dan mengembangkan model baru dan lebih baik untuk keunggulan organisasi. Penerapan model-model ini di sektor korporasi disebut sebagai manajemen ilmiah.

Bidang Terkait

• Analitika Bisnis
• Ilmu Komputer
• Penambangan Data/Ilmu Data/Big Data
• Analisis Keputusan
• Kecerdasan Keputusan
• Teknik Industri
• Rekayasa Keuangan
• Peramalan
• Teori Permainan
• Geografi/Ilmu Informasi Geografis
• Teori Graf
• Pengendalian Inventaris
• Logistik
• Pemodelan Matematika
• Optimisasi Matematika
• Probabilitas dan Statistik
• Manajemen Proyek
• Analisis Kebijakan
• Teori Antrian
• Simulasi
• Jaringan Sosial/Model Peramalan Transportasi
• Proses Stokastik
• Manajemen Rantai Pasokan
• Rekayasa Sistem

Aplikasi

Aplikasi operasional research sangat melimpah, digunakan dalam industri penerbangan, perusahaan manufaktur, organisasi layanan, cabang militer, dan pemerintahan. Berbagai masalah dan isu yang telah memberikan wawasan dan solusi sangat luas. Beberapa di antaranya melibatkan penerapan riset operasi mencakup perencanaan (misalnya di maskapai penerbangan, kereta api dan bus), alokasi (termasuk penempatan kru di penerbangan, kereta api atau bus, serta penugasan karyawan untuk proyek dan komitmen energi serta penempatan untuk fasilitas).

Pembangkitan), Lokasi Fasilitas (termasuk menentukan lokasi yang paling tepat untuk fasilitas baru, seperti gudang, pabrik, atau stasiun pemadam kebakaran), Konstruksi Air dan Perpipaan (melibatkan pengendalian aliran air dari gudang), Pelayanan Kesehatan(dengan Penekanan pada informasi dan manajemen rantai pasokan), teori permainan (mengidentifikasi, memahami, dan mengembangkan strategi bisnis), perencanaan kota, teknik jaringan komputer (termasuk routing, sinkronisasi, dan analisis paket), dan teknik telekomunikasi dan komunikasi data (termasuk routing, sinkronisasi, dan analisis paket). Analisis).

Manajemen juga memperhatikan analisis operasional yang bersifat "soft," yang melibatkan metode perencanaan strategis, dukungan keputusan strategis, dan metode pemodelan masalah. Dalam menghadapi tantangan semacam ini, pemodelan matematis dan simulasi mungkin tidak sesuai atau tidak mencukupi. Oleh karena itu, selama 30 tahun terakhir, sejumlah metode pemodelan non-kuantitatif telah dikembangkan, termasuk pendekatan berbasis pemangku kepentingan, termasuk analisis metagame dan teori drama, analisis morfologis dan berbagai bentuk diagram pengaruh, pemetaan kognitif, pilihan strategis, dan analisis ketahanan.

Disadur dari: en.wikipedia.org

Masalah Optimisasi

Dalam matematika, rekayasa, ilmu komputer, dan ekonomi, masalah optimisasi adalah masalah untuk menemukan solusi terbaik dari semua solusi yang mungkin.Masalah optimisasi dapat dibagi menjadi dua kategori, tergantung pada apakah variabelnya bersifat kontinu atau diskrit.

Masalah optimisasi dengan variabel diskrit dikenal sebagai optimisasi diskrit, di mana objek seperti bilangan bulat, permutasi, atau graf harus ditemukan dari himpunan yang dapat dihitung. Masalah dengan variabel kontinu dikenal sebagai optimisasi kontinu, di mana nilai optimal dari fungsi kontinu harus ditemukan. Ini dapat mencakup masalah terbatas dan masalah multimodal.

Masalah Optimisasi Kontinu

Salah satu contoh masalah optimisasi kontinu adalah masalah minimasi fungsi matematis yang bersifat kontinu. Misalkan kita memiliki fungsi matematis f(x) di mana (x) adalah variabel kontinu. Tujuan dari masalah optimisasi kontinu ini adalah untuk menemukan nilai variabel (x) yang membuat fungsi (f(x)) mencapai nilai minimum.

Contoh konkretnya bisa berupa fungsi kuadrat sederhana seperti (f(x) = x^2) atau fungsi lebih kompleks seperti fungsi kekakuan struktur dalam rekayasa sipil atau fungsi biaya produksi dalam ekonomi. Dalam konteks ini, variabel (x) bisa mewakili panjang, lebar, tinggi, atau parameter lain yang mempengaruhi kinerja atau biaya.

Sebagai contoh, jika (f(x) = x^2), masalah optimisasi kontinu ini akan mencari nilai (x) yang membuat (f(x)) mencapai nilai minimum. Dalam kasus ini, solusi optimalnya adalah (x = 0), karena (f(0) = 0 ) merupakan nilai minimum dari fungsi (f(x)).

Masalah optimasi kombinatorial

Salah satu contoh masalah optimisasi kombinatorial adalah "Traveling Salesman Problem" (TSP). Dalam masalah ini, seorang penjual harus mengunjungi sejumlah kota dan kembali ke kota awal dengan menjelajahi rute terpendek yang mungkin. Penyelesaian dari masalah ini adalah urutan kunjungan yang menghasilkan jarak tempuh total yang minimum.

Misalkan ada enam kota (A, B, C, D, E, F) dan jarak antar kota adalah sebagai berikut:
- A ke B: 10
- A ke C: 15
- A ke D: 20
- B ke C: 25
- B ke D: 30
- C ke D: 35
- B ke E: 40
- C ke E: 45
- D ke E: 50
- B ke F: 55
- C ke F: 60
- D ke F: 65
- E ke F: 70

TSP berusaha menemukan urutan kunjungan kota yang meminimalkan total jarak tempuh. Dalam hal ini, solusi optimal mungkin adalah rute ABCDEF dengan jarak total 170.

Masalah optimisasi kombinatorial sering muncul dalam berbagai konteks, seperti penjadwalan, rute optimal, dan pengaturan tugas. Pencarian solusi optimal dalam masalah ini dapat melibatkan berbagai teknik algoritmik, seperti algoritma genetika, algoritma pencarian terarah, atau algoritma berbasis pohon pencarian.

Disadur dari: en.wikipedia.org

Optimasi kawanan partikel

Dalam ilmu komputer, optimasi gerombolan partikel (PSO) adalah metode komputasi yang bertujuan untuk meningkatkan kandidat solusi secara berulang dengan mempertimbangkan ukuran kualitas tertentu. Metode ini memecahkan masalah dengan memanipulasi populasi kandidat solusi, yang disebut partikel, dan memindahkan partikel-partikel tersebut dalam ruang pencarian berdasarkan rumus matematika sederhana yang menggambarkan posisi dan kecepatan partikel. Pergerakan setiap partikel dipengaruhi oleh posisi lokalyang paling terkenal, namun juga diarahkan ke posisi paling terkenal di ruang pencarian, yang diperbarui saat partikel lain menemukan posisi yang lebih baik. Tujuannya adalah untuk memimpin kelompok menuju solusi terbaik.

PSO awalnya dikaitkan dengan Kennedy, Eberhart dan Shi dan pada awalnya dimaksudkan untuk mensimulasikan perilaku sosial, mewakili pergerakan organisme dalam kawanan burung atau gerombolan ikan.Algoritma tersebut kemudian disederhanakan dan diamati untuk melakukan optimasi. Buku Kennedy dan Eberhart menjelaskan banyak aspek filosofis PSO dan badan intelijen mafia. Poli melakukan survei komprehensif terhadap permintaan PSO. Baru-baru ini, Bonyadi dan Michalewicz menerbitkan tinjauan komprehensif karya teoretis dan eksperimental tentang PSO.

PSO bersifat metaheuristik karena membuat sedikit atau tidak ada asumsi mengenai masalah yang sedang dioptimalkan dan dapat mencari solusi yang mungkin dalam ruang yang sangat luas. Selain itu, PSO tidak menggunakan gradien dari masalah yang sedang dioptimalkan, sehingga masalah optimasi tidak perlu dapat dibedakan, seperti yang disyaratkan oleh metode optimasi klasik seperti metode penurunan gradien dan metode quasi-Newton. Namun perlu diperhatikan bahwa metaheuristik seperti PSO tidak menjamin akan ditemukannya solusi optimal.

Pemlihan Parameter

Pemilihan parameter PSO mempunyai pengaruh yang signifikan terhadap kinerja optimasi. Oleh karena itu, penelitian tentang pemilihan parameter PSO yang mencapai kinerja optimal menjadi fokus utama. Untuk menghindari divergensi (“ledakan”), bobot inersia harus kurang dari 1. Dua parameter lainnya dapat diturunkan dengan menggunakan pendekatan restriktif atau dipilih secara bebas, namun analisis menyarankan wilayah konvergensi untuk membatasinya pada nilai-nilai tipikal. berada dalam kisaran [1,3].Parameter PSO juga dapat dioptimalkan menggunakan pengoptimal overlay lainnya, sebuah konsep yang dikenal sebagai meta-optimasi, atau bahkan disempurnakan selama optimasi, misalnya dengan menggunakan logika fuzzy.Pemilihan parameter PSO juga dapat disesuaikan untuk skenario optimasi yang berbeda.

Lingkungan dan Topologi

Topologi gerombolan mendefinisikan subset partikel yang dapat bertukar informasi dengan setiap partikel. Versi dasar dari algoritma ini menggunakan topologi global sebagai struktur komunikasi cluster. Topologi ini memungkinkan semua partikel untuk berkomunikasi dengan partikel lainnya, sehingga seluruh gerombolan berbagi posisi terbaik yang sama (g) dari satu partikel. Namun, pendekatan ini dapat mengakibatkan kawanan ternak terjebak dalam kondisi minimum lokal. Oleh karena itu,topologi berbeda digunakan untuk mengontrol aliran informasi antar partikel.

Misalnya, dalam topologi lokal, sebuah partikel hanya berbagi informasi dengan subset partikel, di mana subset tersebut adalah subset geometris, seperti "m partikel terdekat", atau subset sosial, yaitu sekelompok partikel yang tidak bergantung pada semua jarak.Dalam kasus seperti ini, varian PSO dianggap yang terbaik secara lokal (dibandingkan dengan varian global dari PSO dasar).Topologi cluster yang umum digunakan adalah ring dimana setiap partikel hanya memiliki dua tetangga, namun terdapat banyak partikel lain di dalam cluster. Topologi belum tentu statis dan upaya telah dilakukan untuk menciptakan topologi adaptif seperti SPSO, APSO, Stochastic Star, TRIBES, Cyber ​​​​​​Swarm dan C-PSO.Dengan menggunakan topologi ring, PSO dapat mencapai paralelisme pada tingkat generasi, sehingga secara signifikan meningkatkan kecepatan evolusi.

Cara Kerja Bagian Dalam

Cara kerja algoritma PSO memiliki pemikiran yang berbeda tentang mengapa dan bagaimana hal itu dapat dioptimalkan.Pandangan umum di kalangan peneliti adalah bahwa perilaku gerombolan bervariasi antara eksplorasi, yang melibatkan pencarian di wilayah ruang pencarian yang lebih luas, dan eksploitasi, yang merupakan pencarian berorientasi lokal untuk mendapatkan titik optimal terdekat (mungkin lokal).

Aliran pemikiran ini telah menjadi konsep umum sejak awal PSO. Aliran pemikiran ini berpendapat bahwa algoritma PSO dan parameternya harus dipilih sedemikian rupa sehingga dapat menyeimbangkan eksplorasi dan eksploitasi untuk menghindari konvergensi dini ke optimal lokal sekaligus memastikan tingkat konvergensi yang baik. Keyakinan ini menjadi dasar dari banyak varian PSO.Sebaliknya, aliran pemikiran lain berfokus pada pemahaman perilaku gerombolan PSO dan bagaimana pengaruhnya terhadap kinerja pengoptimalan aktual, khususnya untuk ruang pencarian berdimensi lebih tinggi dan masalah pengoptimalan yang dapat terputus-putus, berisik, dan bervariasi terhadap waktu. Aliran pemikiran ini mencari algoritma dan parameter PSO yang berkinerja baik dalam konteks eksplorasi dan eksploitasi, terlepas dari interpretasi perilaku kawanan. Studi-studi ini telah mengarah pada penyederhanaan algoritma PSO.

Konvergensi

Dalam konteks OSP, konvergensi memiliki dua arti utama. Pertama, konvergensi himpunan solusi terjadi ketika semua partikel berkumpul pada suatu titik di ruang pencarian, yang mungkin optimal atau tidak. Analisis konvergensi urutan solusi telah memberikan pedoman untuk memilih parameter PSO untuk menghindari divergensi kawanan partikel. Meskipun ada kritik terhadap penyederhanaan analisis yang berlebihan, penelitian menunjukkan bahwa penyederhanaan tersebut tidak berdampak pada batas konvergensi.Kedua, konvergensi menuju optimal lokal terjadi ketika posisi terbaik atau paling terkenal dari kawanan mendekati permasalahan optimal lokal tanpa mempertimbangkan perilaku kawanan secara keseluruhan.

Analisis konvergensi terhadap optimum lokal menunjukkan bahwa PSO memerlukan modifikasi tertentu untuk memastikan ditemukannya optimum lokal. Meskipun penentuan kemampuan konvergensi masih bergantung pada hasil empiris, upaya sedang dilakukan untuk mengembangkan strategi “pembelajaran ortogonal” untuk meningkatkan kinerja PSO secara keseluruhan. Tujuan dari strategi ini adalah untuk mendorong konvergensi global yang lebih cepat, solusi berkualitas lebih tinggi, dan ketahanan yang lebih besar. Namun,penelitian ini tidak memberikan bukti teoretis apa pun yang mendukung klaim tersebut.

Mekanisme Adaptif

Tanpa memerlukan keseimbangan antara konvergensi (“eksploitasi”) dan divergensi (“eksplorasi”), mekanisme adaptif dapat diterapkan. Optimasi kawanan partikel adaptif (APSO) memberikan efisiensi pencarian yang lebih baik daripada PSO standar. APSO dapat melakukan pencarian global di seluruh ruang pencarian dengan kecepatan konvergensi yang lebih cepat, memungkinkan kontrol otomatis terhadap bobot inersia, koefisien percepatan, dan parameter algoritmik lainnya pada waktu proses.ini sekaligus meningkatkan efektivitas dan efisiensi pencarian. Selain itu, APSO juga dapat bertindak berdasarkan partikel terbaik global untuk meninggalkan optimal lokal.Meskipun APSO memperkenalkan parameter algoritme baru, tidak diperlukan kompleksitas desain atau implementasi tambahan.Selain itu, PSO dapat secara efisien mengatasi masalah optimasi komputasi intensif dengan memanfaatkan mekanisme evaluasi kesesuaian skala-adaptif.

Varian

Banyak varian bahkan dari algoritma PSO dasar yang dimungkinkan. Misalnya, ada beberapa metode untuk menginisialisasi partikel dan kecepatan, seperti memulai dari kecepatan nol, serta berbagai pendekatan untuk buffering kecepatan, memperbarui pi dan g hanya setelah seluruh gerombolan diperbarui, dan seterusnya. Beberapa pilihan ini dan dampaknya terhadap kinerja telah dibahas dalam literatur.

Peneliti terkemuka telah mengembangkan serangkaian implementasi standar sebagai dasar untuk menguji kinerja teknik peningkatan sekaligus memperkenalkan PSO ke komunitas pengoptimalan yang lebih luas. Keberadaan standar algoritme yang terkenal dan didefinisikan secara ketat memberikan titik perbandingan berharga yang dapat digunakan di seluruh penelitian untuk menguji kemajuan baru dengan lebih baik.Salah satu standar terbaru adalah Standar PSO 2011 (SPSO-2011).

Hibridisasi

Untuk meningkatkan kinerja pengoptimalan, varian PSO baru dan lebih canggih terus diperkenalkan. Terdapat tren tertentu dalam penelitian ini, termasuk pengembangan metode optimasi hybrid yang menggabungkan PSO dengan pengoptimal lainnya. Contoh pendekatan ini antara lain menggabungkan PSO dengan optimasi berbasis biogeografi dan mengintegrasikan metode pembelajaran yang efektif. Tujuan pengembangan varian ini adalah untuk mencapai peningkatan kinerja lebih lanjut dalam proses optimasi dengan menggabungkan keunggulan PSO dengan sifat positif metode optimasi lainnya. Pendekatan ini membuka peluang eksplorasi dan penggunaan yang lebih efisien dalam bidang pencarian solusi.

Mengurangi Kovergensi Dini

Tren penelitian lainnya adalah upaya untuk mengurangi konvergensi dini, yang mengindikasikan stagnasi optimasi. Beberapa pendekatan yang digunakan antara lain membalikkan atau menghentikan pergerakan partikel PSO. Selain itu, strategi lain untuk mengatasi konvergensi prematur adalah dengan menggunakan multiple-swarm (multi-swarm optimizer). Pendekatan multi-swarm juga dapat digunakan untuk mengimplementasikan optimasi multi-tujuan. Selain itu, terdapat kemajuan dalam penyesuaian parameter perilakuPSO selama proses optimasi.Semua ini merupakan upaya untuk meningkatkan ketahanan algoritme terhadap konvergensi dini dan meningkatkan kinerja pengoptimalan pada masalah yang kompleks dan dinamis.

Penyederhanaan

Aliran pemikiran lainnya adalah bahwa PSO harus disederhanakan sebanyak mungkin tanpa mengorbankan kinerjanya, sebuah konsep yang sering disebut sebagai “Occam's Razor.” Kennedy awalnya mengusulkan penyederhanaan PSO, dan penelitian selanjutnya menunjukkan bahwa menyederhanakan PSO meningkatkan kinerja pengoptimalan, mempermudah penyesuaian parameter, dan menjaga konsistensi kinerja di berbagai masalah pengoptimalan.

Argumen untuk menyederhanakan PSO mencakup keyakinan bahwa efektivitas metaheuristik hanya dapat ditunjukkan secara empiris melalui eksperimen komputasi pada sejumlah masalah optimasi yang terbatas. Sulit untuk membuktikan bahwa metaheuristik seperti PSO benar, sehingga meningkatkan risiko kesalahan dalam deskripsi dan implementasinya. Misalnya, varian algoritma genetika menunjukkan potensi besar tetapi kemudian ditemukan cacat karena optimasi pencariannya bias terhadapnilai serupa untuk berbagai dimensi dalam ruang pencarian.Penyederhanaan PSO juga berlaku untuk inisialisasi cepat. Variasi PSO Bare Bones yang diusulkan oleh James Kennedy pada tahun 2003 tidak memerlukan penggunaan kecepatan sama sekali. Varian lain yang lebih sederhana adalah Accelerated Particle Swarm Optimization (APSO), yang juga tidak memerlukan kecepatan dan dapat mempercepat konvergensi di banyak aplikasi. Kode demo APSO sederhana tersedia.

Pengoptimalan Multi-Tujuan

PSO juga telah berhasil diterapkan pada masalah multiobjektif dimana perbandingan fungsi objektif memperhitungkan dominasi Pareto dalam gerak partikel PSO. Dalam konteks ini, solusi yang tidak didominasi disimpan sedemikian rupa sehingga mendekati front Pareto dan memberikan alternatif optimal yang mencakup solusi yang tidak dapat dilampaui satu sama lain dalam konteks fungsi tujuan yang berbeda. 

Disadur dari: en.wikipedia.org

Problem Solving (Pemecahan Masalah)

Pemecahan masalah adalah proses mencapai tujuan dengan mengatasi hambatan yang dapat timbul dalam berbagai aktivitas, mulai dari tugas sederhana hingga permasalahan kompleks dalam bidang bisnis dan teknis. Ada dua klasifikasi utama pemecahan masalah: pemecahan masalah sederhana (SPS), yang menangani satu masalah, dan pemecahan masalah kompleks (CPS), yang melibatkan batasan-batasan yang saling terkait.

Tugas pemecahan masalah juga dapat dibagi menjadi tugas yang terdefinisi dengan jelas denganhambatan dan tujuan tertentu, dan masalah yang tidak jelas sehingga sulit untuk menemukan solusinya. Solusi memerlukan sumber daya dan pengetahuan yang memadai, dan para profesional seperti pengacara, dokter, pemrogram, dan konsultan sering kali bertindak sebagai pemecah masalah. Banyak teknik dan metode pemecahan masalah telah dikembangkan di berbagai bidang seperti teknik, bisnis, kedokteran, matematika, ilmu komputer, filsafat, dan organisasi sosial.Memahami keterbatasan mental seperti bias konfirmasi, struktur mental, dan fiksasi fungsional juga merupakan fokus penting dalam penelitian pemecahan masalah.

Definisi

Istilah pemecahan masalah mempunyai arti yang berbeda-beda tergantung pada disiplin ilmunya. Dalam psikologi mengacu pada proses mental, sedangkan dalam ilmu komputer mengacu pada proses berbasis komputer. Ada dua jenis masalah: masalah yang terdefinisi dengan baik dan masalah yang tidak terdefinisi, yang memerlukan pendekatan berbeda. Masalah yang terdefinisi dengan baik mempunyai tujuan akhir dan solusi yang jelas, sedangkan masalah yang terdefinisi dengan buruk tidak memiliki tujuan akhir yang spesifik. Pemecahan masalah berkaitan dengan pragmatik dan semantik, dimana kunci penyelesaiannya adalah memahami tujuan akhir dan kaidah yang berlaku.Pemecahan masalah melibatkan dua bidang utama: penyelesaian masalah matematika dan penyelesaian masalah pribadi, yang masing-masing mempunyai kesulitan dan hambatan yang berbeda.

Psikologi

Dalam psikologi, pemecahan masalah adalah proses menemukan solusi terhadap permasalahan dalam kehidupan. Proses ini mencakup penemuan dan penetapan masalah, menghasilkan solusi potensial, mengevaluasinya, dan memilih solusi untuk implementasi dan peninjauan. Pemecahan masalah memerlukan modulasi dan pengendalian keterampilan dan melibatkan orientasi masalah, analisis sistematis dan keterampilan pemecahan masalah.

Profesional kesehatan mental menggunakan metode seperti introspeksi, behaviorisme, simulasi, pemodelan komputer, dan eksperimen untuk memahami proses pemecahan masalah manusia. Penelitian empiris menunjukkan bahwa beragam strategi dan faktor mempengaruhi pemecahan masalah sehari-hari, termasuk pengaruh emosi. Menyelesaikan masalah antarpribadi juga bergantung pada motivasi dan konteks pribadi, dan pengendalian emosi yang baik adalah kunci untuk berfokus pada tujuan tugas dan hasil positif. Dalam konseptualisasi, pemecahan masalah manusia melibatkan dua proses terkait: orientasi masalah dan pendekatan motivasi/sikap/afektif terhadap situasi masalah dan keterampilan pemecahan masalah.

Ilmu Kognitif

Psikolog eksperimental, khususnya Gestaltist di Jerman seperti Karl Duncker, Allen Newell, dan Herbert A. Simon, memelopori studi tentang pemecahan masalah. Penelitian eksperimental yang dilakukan pada tahun 1960an dan awal 1970an, yang melibatkan tugas laboratorium yang sederhana namun terdefinisi dengan baik seperti Menara Hanoi, membantu mengungkap keseluruhan proses pemecahan masalah. Para peneliti berhipotesis bahwa pemecahan masalah dalam tugas model ini akan mencerminkan proses kognitif yang juga berperan dalam memecahkan masalah dunia nyata yang lebih kompleks. Sebagai hasil dari penelitian ini, muncullah teknik pemecahan masalah yang penting seperti prinsip dekomposisi.

Ilmu Komputer

Sebagian besar ilmu komputer dan kecerdasan buatan berfokus pada pengembangan sistem otomatis untuk memecahkan masalah dengan menerima masukan data dan dengan cepat menghasilkan jawaban yang benar atau sesuai. Proses desain sistem ini mencakup langkah-langkah seperti penentuan masalah, penggunaan heuristik, analisis akar penyebab, deduplikasi, analisis, diagnosis, dan perbaikan. Algoritma, seperti resep atau instruksi, menjadi panduan untuk menentukan arah sistem dan diterjemahkan ke dalam program komputer. Teknik analisis seperti pemrograman linier dan nonlinier, sistem antrian dan simulasi digunakan. Hambatan utama dalam pengembangan sistem adalah menemukan dan memperbaiki kesalahan dalam program komputer, yang dikenal dengan istilah debugging.

Logika

Logika formal membahas isu-isu seperti validitas, kebenaran, inferensi, argumentasi, dan pembuktian. Dalam konteks pemecahan masalah, istilah ini dapat digunakan untuk menyatakan suatu masalah secara formal sebagai teorema yang perlu dibuktikan. Penggunaan komputer dalam membuktikan teorema matematika menggunakan logika formal muncul sebagai bidang pembuktian teorema otomatis pada tahun 1950-an. Ini melibatkan metode heuristik dan algoritmik, seperti Mesin Teori Logika dan prinsip resolusi. Pembuktian teorema otomatis tidak hanya diterapkan dalam matematika, tetapi juga digunakan untuk verifikasi program dalam ilmu komputer. John McCarthy mengusulkan pengambil nasihat pada tahun 1958, yang menggunakan logika formal untuk merepresentasikan informasi dan menjawab pertanyaan dengan pembuktian teorema otomatis.

Cordell Green pada tahun 1969 mengembangkan metode resolusi, yang digunakan dalam pembuktian teorema otomatis dan aplikasi kecerdasan buatan seperti perencanaan robot. Meskipun mendapat kritik, Robert Kowalski mengembangkan pemrograman logika dan resolusi SLD untuk memecahkan masalah dengan dekomposisi, menganjurkan penggunaan logika dalam pemecahan masalah komputer dan manusia, serta logika komputasi untuk meningkatkan pemikiran manusia.

Rekayasa

Jika suatu produk atau proses gagal, teknik pemecahan masalah dapat digunakan secara reaktif untuk mengidentifikasi tindakan perbaikan dan mencegah kegagalan di masa depan. Teknik-teknik ini dapat diterapkan secara proaktif sebelum terjadi kegagalan untuk memprediksi, menganalisis, dan memitigasi potensi masalah. Mode kegagalan dan analisis dampak adalah contoh teknik proaktif yang dapat mengurangi risiko masalah. Dalam kedua pendekatan tersebut, penjelasan sebab akibat harus dikembangkan melalui proses diagnostik.

Proses ini mencakup pembangkitan ide atau hipotesis baru, inferensi untuk mengevaluasi dan menyempurnakan hipotesis, dan induksi untuk membenarkan hipotesis dengan data empiris.Tujuan penculikan adalah untuk menentukan hipotesis yang akan diuji, bukan untuk mengadopsi atau mengkonfirmasinya. Dalam logika Peircean, penculikan dan deduksi berkontribusi pada pemahaman konseptual, sementara induksi menambahkan detail kuantitatif pada pengetahuan konseptual. Teknologi forensik digunakan untuk menganalisis kesalahan dengan mendeteksi cacat produk dan mengambil tindakan perbaikan untuk mencegah kesalahan di masa depan. Sebaliknya, rekayasa balik berupaya menemukan logika pemecahan masalah aslidengan membongkar produk dan mengembangkan cara logis untuk memproduksi dan merakit bagian-bagiannya.

Disadur dari: en.wikipedia.org