Sistem nonlinier
Sistem nonlinier dalam matematika dan sains adalah sistem yang perubahan keluarannya tidak sebanding dengan perubahan masukan. Masalah nonlinier menarik perhatian para insinyur, ahli biologi, fisikawan, matematikawan, dan ilmuwan lain karena sebagian besar sistem pada dasarnya bersifat nonlinier. Sistem nonlinier dalam matematika dapat dijelaskan dengan sistem persamaan nonlinier, yaitu kumpulan persamaan simultan yang variabel-variabelnya tidak diketahui muncul sebagai variabel polinomial berderajatlebih besar dari satu atau sebagai argumen fungsi yang bukan polinomial berderajat satu. Karena persamaan dalam sistem nonlinier tidak dapat ditulis sebagai kombinasi linier dari variabel atau fungsi yang tidak diketahui yang muncul di dalamnya, sistem tersebut dapat dianggap nonlinier meskipun fungsi linier yang diketahui muncul dalam persamaan tersebut.
Secara umum, suatu persamaan diferensial dianggap linier jika persamaan tersebut linier terhadap fungsi yang tidak diketahui dan turunannya, meskipun persamaan tersebut mungkin nonlinier terhadapvariabel lain yang muncul di dalamnya.Karena persamaan diferensial dinamis nonlinier sulit diselesaikan, sistem nonlinier biasanya didekati dengan persamaan linier (linierisasi). Ini bekerja dengan baik hingga tingkat presisi dan rentang nilai masukan tertentu, tetapi beberapa fenomena menarik seperti soliton, chaos, dan singularitas disembunyikan oleh linearisasi. Oleh karena itu, beberapa aspek perilaku dinamis sistem nonlinier mungkin tampak berlawanan dengan intuisi, tidak dapat diprediksi, atau bahkan kacau. Meskipun perilaku kacaumungkin menyerupai perilaku acak, sebenarnya perilaku tersebut tidak acak. Misalnya, beberapa aspek iklim tampak kacau, dengan perubahan sederhana pada satu bagian sistem mempunyai dampak kompleks pada keseluruhan sistem.Ketidaklinieran ini adalah salah satu alasan mengapa perkiraan jangka panjang yang akurat tidak mungkin dilakukan dengan teknologi saat ini.
Persamaan aljabar nonlinier
Persamaan aljabar nonlinier, disebut juga persamaan polinomial, didefinisikan dengan menyamakan polinomial (yang derajatnya lebih besar dari satu) menjadi nol. Sebagai contoh,
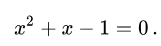
Algoritme pencarian akar dapat digunakan untuk mencari solusi unik persamaan polinomial (yaitu himpunan nilai variabel yang memenuhi persamaan tersebut). Namun, sistem persamaan aljabar lebih kompleks; Studinya menjadi motivasi untuk bidang geometri aljabar, cabang matematika modern yang sulit. Sulit juga menentukan apakah sistem aljabar mempunyai solusi kompleks (lihat teorema nol Hilbert). Namun, untuk sistem dengan jumlah solusi kompleks yang terbatas,sistem persamaan polinomial ini sekarang telah dipahami dengan baik dan terdapat metode yang efisien untuk menyelesaikannya.
Hubungan perulangan nonlinier
Relasi perulangan nonlinier mendefinisikan barisan suku-suku dalam suatu barisan sebagai fungsi nonlinier dari suku-suku sebelumnya. Contoh hubungan perulangan nonlinier mencakup peta logistik dan hubungan yang menentukan berbagai rangkaian Hofstadter. Model nonlinier diskrit, yang mewakili kelas luas hubungan perulangan nonlinier, mencakup model NARMAX (Nonlinear Autoregressive Moving Average dengan Input Eksogen) dan metode terkait untuk mengidentifikasi dan menganalisis sistem nonlinier.Pendekatan ini dapat digunakan untuk mempelajari berbagai perilaku nonlinier kompleks dalam domain waktu, frekuensi, dan spatiotemporal.
Persamaan diferensial nonlinier
Suatu sistem persamaan diferensial tergolong nonlinier jika bukan merupakan sistem persamaan linier. Masalah persamaan diferensial nonlinier sangat beragam dan cara penyelesaiannya bergantung pada sifat masalahnya. Persamaan Navier-Stokes dalam dinamika fluida dan persamaan Lotka-Volterra dalam biologi merupakan contoh persamaan diferensial nonlinier. Tantangan terbesar dalam permasalahan nonlinier adalah sulitnya menggabungkan solusi yang sudah diketahui menjadi solusi baru karena tidak adanya prinsip superposisi seperti pada permasalahan linier. Meskipun beberapa solusi khusus dapat ditemukan untuk persamaan nonlinier, prinsip superposisi yang buruk menyulitkan pembuatan solusi baru.
Persamaan diferensial parsial
Saat mempelajari persamaan diferensial parsial nonlinier, pendekatan dasar yang paling umum adalah mengubah variabel (atau soal) sehingga soal yang dihasilkan lebih sederhana, mungkin linier. Terkadang persamaan tersebut dapat diubah menjadi satu atau lebih persamaan diferensial biasa, seperti dalam metode pemisahan variabel, yang selalu berguna terlepas dari apakah persamaan diferensial biasa yang dihasilkan mempunyai solusi atau tidak.Taktik lain yang umum, meskipun kurang matematis, yang sering digunakan dalam mekanika termal dan fluida adalah melakukan analisis penskalaan untuk menyederhanakan persamaan natural umum dalam masalah nilai batas tertentu.
Misalnya, dalam kasus aliran satu dimensi, laminar, transien dalam pipa melingkar, persamaan Navier-Stokes yang sangat nonlinier dapat disederhanakan menjadi persamaan diferensial parsial linier; Analisis penskalaan memberikan kondisi di mana aliran bersifat laminar dan satu dimensi serta menghasilkan persamaan yang disederhanakan.Metode lainnya adalah mempelajari sifat-sifat dan menerapkan metode persamaan diferensial biasa yang dijelaskan di atas.
Disadur dari : en.wikipedia.org