Kontrol proses statistik (SPC) adalah metode kontrol kualitas yang menggunakan metode statistik untuk memantau dan mengendalikan suatu proses. Ini membantu memastikan bahwa proses beroperasi secara efisien, menghasilkan lebih banyak produk yang sesuai dengan spesifikasi dengan lebih sedikit limbah (pengerjaan ulang atau skrap). SPC dapat diterapkan pada proses apa pun di mana output "produk yang sesuai" (produk yang memenuhi spesifikasi) dapat diukur. Alat utama yang digunakan dalam SPC termasuk grafik lari, grafik kontrol, fokus pada peningkatan berkelanjutan, dan desain eksperimen. Contoh proses di mana SPC diterapkan adalah jalur manufaktur.

SPC harus dipraktekkan dalam dua fase: Fase pertama adalah pembentukan awal proses, dan fase kedua adalah penggunaan proses produksi secara teratur. Pada fase kedua, keputusan periode yang akan diperiksa harus dibuat, tergantung pada perubahan kondisi 5M&E (Man, Machine, Material, Method, Movement, Environment) dan tingkat keausan suku cadang yang digunakan dalam proses manufaktur (suku cadang mesin , jig, dan perlengkapan).

Keuntungan SPC dibandingkan metode kontrol kualitas lainnya, seperti "inspeksi", adalah bahwa metode ini menekankan deteksi dini dan pencegahan masalah, daripada koreksi masalah setelah terjadi.

Selain mengurangi pemborosan, SPC dapat mengurangi waktu yang dibutuhkan untuk menghasilkan produk. SPC memperkecil kemungkinan produk jadi perlu dikerjakan ulang atau dibuang.

Sejarah

Kontrol proses statistik dipelopori oleh Walter A. Shewhart di Bell Laboratories pada awal 1920-an. Shewhart mengembangkan peta kendali pada tahun 1924 dan konsep keadaan kendali statistik. Kontrol statistik setara dengan konsep pertukaran[1][2] yang dikembangkan oleh ahli logika William Ernest Johnson juga pada tahun 1924 dalam bukunya Logic, Part III: The Logical Foundations of Science.[3] Bersama dengan tim di AT&T yang mencakup Harold Dodge dan Harry Romig, ia juga bekerja untuk menempatkan inspeksi pengambilan sampel pada basis statistik yang rasional. Shewhart berkonsultasi dengan Kolonel Leslie E. Simon dalam penerapan peta kendali untuk pembuatan amunisi di Picatinny Arsenal Angkatan Darat pada tahun 1934. Penerapan yang berhasil itu membantu meyakinkan Ordnance Angkatan Darat untuk melibatkan George Edwards dari AT&T untuk berkonsultasi tentang penggunaan kendali mutu statistik di antara divisi-divisinya dan kontraktor pada pecahnya Perang Dunia II.

W. Edwards Deming mengundang Shewhart untuk berbicara di Sekolah Pascasarjana Departemen Pertanian AS dan menjabat sebagai editor buku Shewhart Statistical Method from the Viewpoint of Quality Control (1939), yang merupakan hasil dari kuliah tersebut. Deming adalah arsitek penting kursus singkat kendali mutu yang melatih industri Amerika dalam teknik-teknik baru selama Perang Dunia II. Lulusan kursus masa perang ini membentuk masyarakat profesional baru pada tahun 1945, American Society for Quality Control, yang memilih Edwards sebagai presiden pertamanya. Deming melakukan perjalanan ke Jepang selama Pendudukan Sekutu dan bertemu dengan Persatuan Ilmuwan dan Insinyur Jepang (JUSE) dalam upaya untuk memperkenalkan metode SPC ke industri Jepang.[4][5]

Sumber variasi 'umum' dan 'khusus'

Shewhart membaca teori statistik baru yang keluar dari Inggris, terutama karya William Sealy Gosset, Karl Pearson, dan Ronald Fisher. Namun, dia mengerti bahwa data dari proses fisik jarang menghasilkan kurva distribusi normal (yaitu, distribusi Gaussian atau 'kurva lonceng'). Dia menemukan bahwa data dari pengukuran variasi di bidang manufaktur tidak selalu berperilaku seperti data dari pengukuran fenomena alam (misalnya, gerakan partikel Brown). Shewhart menyimpulkan bahwa sementara setiap proses menampilkan variasi, beberapa proses menampilkan variasi yang wajar bagi proses (sumber variasi "umum"); proses-proses ini ia gambarkan berada dalam kendali (statistik). Proses lain juga menampilkan variasi yang tidak ada dalam sistem kausal dari proses sepanjang waktu (sumber variasi "khusus"), yang digambarkan Shewhart sebagai tidak terkendali.

Aplikasi untuk proses non-manufaktur

Kontrol proses statistik sesuai untuk mendukung setiap proses berulang, dan telah diterapkan di banyak pengaturan di mana misalnya sistem manajemen mutu ISO 9000 digunakan, termasuk audit keuangan dan akuntansi, operasi TI, proses perawatan kesehatan, dan proses administrasi seperti pengaturan pinjaman dan administrasi, penagihan pelanggan, dll. Terlepas dari kritik atas penggunaannya dalam desain dan pengembangan, ini adalah tempat yang tepat untuk mengelola tata kelola data semi-otomatis dari operasi pemrosesan data volume tinggi, misalnya di gudang data perusahaan, atau manajemen kualitas data perusahaan sistem. [7]

Dalam Capability Maturity Model (CMM) 1988, Institut Rekayasa Perangkat Lunak menyarankan agar SPC dapat diterapkan pada proses rekayasa perangkat lunak. Praktek Level 4 dan Level 5 dari Capabil ity Maturity Model Integration (CMMI) menggunakan konsep ini.

Penerapan SPC untuk non-repetitive, proses pengetahuan-intensif, seperti penelitian dan pengembangan atau rekayasa sistem, telah menghadapi skeptisisme dan tetap kontroversial.

Dalam No Silver Bullet, Fred Brooks menunjukkan bahwa kompleksitas, persyaratan kesesuaian, kemampuan berubah, dan ketidaktampakan perangkat lunak menghasilkan variasi yang melekat dan esensial yang tidak dapat dihilangkan. Ini menyiratkan bahwa SPC kurang efektif dalam pengembangan perangkat lunak daripada di, misalnya, manufaktur.

Variasi dalam pembuatan

Dalam manufaktur, kualitas didefinisikan sebagai kesesuaian dengan spesifikasi. Namun, tidak ada dua produk atau karakteristik yang sama persis, karena setiap proses mengandung banyak sumber variabilitas. Dalam pembuatan massal, secara tradisional, kualitas barang jadi dipastikan dengan inspeksi produk pasca-manufaktur. Setiap artikel (atau sampel artikel dari lot produksi) dapat diterima atau ditolak sesuai dengan seberapa baik memenuhi spesifikasi desainnya, SPC menggunakan alat statistik untuk mengamati kinerja proses produksi untuk mendeteksi variasi yang signifikan sebelum menghasilkan produksi barang di bawah standar. Setiap sumber variasi pada setiap titik waktu dalam suatu proses akan jatuh ke dalam salah satu dari dua kelas.

(1) Penyebab umum

Penyebab 'umum' kadang-kadang disebut sebagai sumber variasi 'tidak dapat ditentukan', atau 'normal'. Ini mengacu pada sumber variasi apa pun yang secara konsisten bertindak pada proses, yang biasanya ada banyak. Jenis penyebab ini secara kolektif menghasilkan distribusi yang stabil secara statistik dan berulang dari waktu ke waktu.

(2) Penyebab khusus

Penyebab 'khusus' kadang-kadang disebut sebagai sumber variasi yang 'dapat dialihkan'. Istilah ini mengacu pada setiap faktor yang menyebabkan variasi yang hanya mempengaruhi beberapa keluaran proses. Mereka sering terputus-putus dan tidak dapat diprediksi.

Sebagian besar proses memiliki banyak sumber variasi; kebanyakan dari mereka adalah kecil dan dapat diabaikan. Jika sumber variasi yang dapat ditetapkan yang dominan terdeteksi, berpotensi mereka dapat diidentifikasi dan dihilangkan. Ketika mereka dihapus, prosesnya dikatakan 'stabil'. Ketika suatu proses stabil, variasinya harus tetap dalam batas-batas yang diketahui. Yaitu, setidaknya, sampai sumber variasi lain yang dapat ditentukan terjadi.

Misalnya, lini pengemasan sereal sarapan dapat dirancang untuk mengisi setiap kotak sereal dengan 500 gram sereal. Beberapa kotak akan memiliki sedikit lebih dari 500 gram, dan beberapa akan memiliki sedikit lebih sedikit. Ketika berat paket diukur, data akan menunjukkan distribusi berat bersih.

Jika proses produksi, inputnya, atau lingkungannya (misalnya, mesin on line) berubah, distribusi data akan berubah. Misalnya, karena cam dan puli mesin aus, mesin pengisi sereal dapat memasukkan lebih dari jumlah sereal yang ditentukan ke dalam setiap kotak. Meskipun ini mungkin menguntungkan pelanggan, dari sudut pandang produsen, hal itu boros, dan meningkatkan biaya produksi. Jika pabrikan menemukan perubahan dan sumbernya pada waktu yang tepat, perubahan tersebut dapat diperbaiki (misalnya, cam dan puli diganti).

Dari perspektif SPC, jika berat setiap kotak sereal bervariasi secara acak, beberapa lebih tinggi dan beberapa lebih rendah, selalu dalam kisaran yang dapat diterima, maka proses tersebut dianggap stabil. Jika cam dan puli mesin mulai aus, bobot kotak sereal mungkin tidak acak. Fungsi cam dan puli yang menurun dapat menyebabkan pola linier non-acak dari peningkatan bobot kotak sereal. Kami menyebutnya variasi penyebab umum. Namun, jika semua kotak sereal tiba-tiba beratnya lebih dari rata-rata karena kerusakan tak terduga dari cams dan puli, ini akan dianggap sebagai variasi penyebab khusus.

Aplikasi

Penerapan SPC melibatkan tiga fase kegiatan utama:

1. Memahami proses dan batasan spesifikasi.
2. Menghilangkan sumber variasi yang dapat dialihkan (khusus), sehingga prosesnya stabil.
3. Memantau proses produksi yang sedang berjalan, dibantu dengan penggunaan peta kendali, untuk mendeteksi perubahan yang signifikan dari rata-rata atau variasi.

Bagan kendali

Data dari pengukuran variasi pada titik-titik pada peta proses dipantau menggunakan diagram kendali. Bagan kontrol berusaha membedakan sumber variasi yang "dapat ditetapkan" ("khusus") dari sumber "umum". Sumber "umum", karena merupakan bagian yang diharapkan dari proses, tidak terlalu diperhatikan oleh pabrikan daripada sumber "dapat dialihkan". Menggunakan diagram kendali adalah aktivitas yang berkelanjutan, terus-menerus dari waktu ke waktu.

Proses yang stabil

Ketika proses tidak memicu salah satu "aturan deteksi" bagan kontrol untuk bagan kontrol, itu dikatakan "stabil". Analisis kemampuan proses dapat dilakukan pada proses yang stabil untuk memprediksi kemampuan proses untuk menghasilkan "produk yang sesuai" di masa depan.

Proses yang stabil dapat ditunjukkan dengan tanda tangan proses yang bebas dari varians di luar indeks kemampuan. Tanda tangan proses adalah titik-titik yang diplot dibandingkan dengan indeks kemampuan.

Variasi berlebihan

Ketika proses memicu salah satu dari "aturan deteksi" bagan kontrol (atau sebagai alternatif, kemampuan proses rendah), aktivitas lain dapat dilakukan untuk mengidentifikasi sumber variasi yang berlebihan. Alat yang digunakan dalam kegiatan ekstra ini meliputi: diagram Ishikawa, eksperimen yang dirancang, dan diagram Pareto. Eksperimen yang dirancang adalah sarana untuk mengukur secara objektif kepentingan relatif (kekuatan) sumber variasi. Setelah sumber variasi (penyebab khusus) diidentifikasi, mereka dapat diminimalkan atau dihilangkan. Langkah-langkah untuk menghilangkan sumber variasi mungkin termasuk: pengembangan standar, pelatihan staf, pemeriksaan kesalahan, dan perubahan pada proses itu sendiri atau inputnya.

Metrik stabilitas proses

Saat memantau banyak proses dengan diagram kendali, terkadang berguna untuk menghitung ukuran kuantitatif stabilitas proses. Metrik ini kemudian dapat digunakan untuk mengidentifikasi/memprioritaskan proses yang paling membutuhkan tindakan korektif. Metrik ini juga dapat dilihat sebagai pelengkap metrik kemampuan proses tradisional. Beberapa metrik telah diusulkan, seperti yang dijelaskan dalam Ramirez dan Runger. Yaitu (1) Rasio Stabilitas yang membandingkan variabilitas jangka panjang dengan variabilitas jangka pendek, (2) Uji ANOVA yang membandingkan variasi dalam-subkelompok dengan variasi antar-subkelompok, dan (3) Rasio Ketidakstabilan yang membandingkan jumlah subgrup yang memiliki satu atau lebih pelanggaran aturan Western Electric dengan jumlah total subgrup.

Matematika diagram kendali

Bagan kendali digital menggunakan aturan berbasis logika yang menentukan "nilai turunan" yang menandakan perlunya koreksi. Sebagai contoh,

nilai turunan = nilai terakhir + selisih absolut rata-rata antara N angka terakhir.

Sumber Artikel: en.wikipedia.org

Dalam analisis numerik, mendaki bukit adalah teknik optimasi matematis yang termasuk dalam keluarga pencarian lokal. Ini adalah algoritma iteratif yang dimulai dengan solusi arbitrer untuk suatu masalah, kemudian mencoba menemukan solusi yang lebih baik dengan membuat perubahan bertahap pada solusi. Jika perubahan menghasilkan solusi yang lebih baik, perubahan tambahan lainnya dilakukan pada solusi baru, dan seterusnya sampai tidak ada perbaikan lebih lanjut yang dapat ditemukan.

Misalnya, mendaki bukit dapat diterapkan pada masalah salesman keliling. Sangat mudah untuk menemukan solusi awal yang mengunjungi semua kota tetapi kemungkinan akan sangat buruk dibandingkan dengan solusi optimal. Algoritme dimulai dengan solusi semacam itu dan membuat perbaikan kecil untuknya, seperti mengubah urutan kunjungan dua kota. Akhirnya, rute yang jauh lebih pendek kemungkinan akan diperoleh.

Pendakian bukit menemukan solusi optimal untuk masalah cembung – untuk masalah lain hanya akan menemukan optima lokal (solusi yang tidak dapat diperbaiki oleh konfigurasi tetangga), yang belum tentu solusi terbaik (optimal global) dari semua solusi yang mungkin ( ruang pencarian). Contoh algoritma yang memecahkan masalah cembung dengan mendaki bukit termasuk algoritma simpleks untuk pemrograman linier dan pencarian biner.: 253  Untuk mencoba menghindari terjebak dalam optima lokal, seseorang dapat menggunakan restart (yaitu pencarian lokal berulang), atau lebih skema kompleks berdasarkan iterasi (seperti pencarian lokal berulang), atau pada memori (seperti optimasi pencarian reaktif dan pencarian tabu), atau pada modifikasi stokastik tanpa memori (seperti simulasi anil).

Kesederhanaan relatif dari algoritme menjadikannya pilihan pertama yang populer di antara algoritme pengoptimalan. Ini digunakan secara luas dalam kecerdasan buatan, untuk mencapai keadaan tujuan dari simpul awal. Pilihan yang berbeda untuk node berikutnya dan node awal digunakan dalam algoritma terkait. Meskipun algoritme yang lebih canggih seperti simulasi anil atau pencarian tabu dapat memberikan hasil yang lebih baik, dalam beberapa situasi mendaki bukit juga berfungsi dengan baik. Pendakian bukit seringkali dapat menghasilkan hasil yang lebih baik daripada algoritma lain ketika jumlah waktu yang tersedia untuk melakukan pencarian terbatas, seperti dengan sistem waktu nyata, selama sejumlah kecil peningkatan biasanya menyatu pada solusi yang baik (solusi optimal atau pendekatan dekat). Di sisi lain, bubble sort dapat dilihat sebagai algoritme pendakian bukit (setiap pertukaran elemen yang berdekatan mengurangi jumlah pasangan elemen yang tidak teratur), namun pendekatan ini jauh dari efisien bahkan untuk N yang sederhana, karena jumlah pertukaran yang diperlukan bertambah secara kuadrat.

Mendaki bukit adalah algoritme kapan saja: ia dapat mengembalikan solusi yang valid bahkan jika terputus kapan saja sebelum berakhir.

Deskripsi matematika

Mendaki bukit mencoba untuk memaksimalkan (atau meminimalkan) fungsi target , di mana adalah vektor nilai kontinu dan/atau diskrit. Pada setiap iterasi, mendaki bukit akan menyesuaikan satu elemen di dan menentukan apakah perubahan meningkatkan nilai . (Perhatikan bahwa ini berbeda dari metode penurunan gradien, yang menyesuaikan semua nilai dalam pada setiap iterasi sesuai dengan gradien bukit.) Dengan mendaki bukit, perubahan apa pun yang meningkatkan diterima, dan proses berlanjut sampai tidak ada perubahan yang dapat ditemukan untuk meningkatkan nilai. Maka dikatakan "optimal secara lokal".

Dalam ruang vektor diskrit, setiap nilai yang mungkin untuk  dapat divisualisasikan sebagai simpul dalam graf. Pendakian bukit akan mengikuti grafik dari titik ke titik, selalu meningkat (atau menurun) secara lokal nilai , hingga maksimum lokal (atau minimum lokal ) tercapai.

Varian

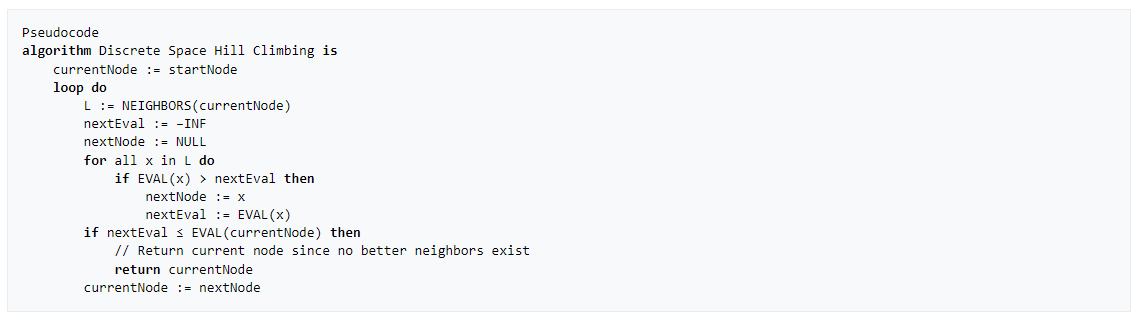
Dalam pendakian bukit sederhana, simpul terdekat pertama dipilih, sedangkan pada pendakian bukit tercuram semua penerus dibandingkan dan yang paling dekat dengan solusi dipilih. Kedua bentuk gagal jika tidak ada node yang lebih dekat, yang mungkin terjadi jika ada maxima lokal di ruang pencarian yang bukan solusi. Pendakian bukit pendakian terjal mirip dengan pencarian terbaik-pertama, yang mencoba semua kemungkinan ekstensi jalur saat ini, bukan hanya satu.

Pendakian bukit stokastik tidak memeriksa semua tetangga sebelum memutuskan bagaimana cara bergerak. Sebaliknya, ia memilih tetangga secara acak, dan memutuskan (berdasarkan jumlah peningkatan pada tetangga itu) apakah akan pindah ke tetangga itu atau memeriksa yang lain.

Penurunan koordinat melakukan pencarian garis sepanjang satu arah koordinat pada titik saat ini di setiap iterasi. Beberapa versi penurunan koordinat secara acak memilih arah koordinat yang berbeda masing-masing erasi.

Pendakian bukit yang dimulai ulang secara acak adalah meta-algoritma yang dibangun di atas algoritma pendakian bukit. Ini juga dikenal sebagai pendakian bukit Shotgun. Ini secara iteratif melakukan pendakian bukit, setiap kali dengan kondisi awal acak . terbaik dipertahankan: jika rangkaian baru mendaki bukit menghasilkan yang lebih baik daripada status tersimpan, ini akan menggantikan status tersimpan.

Pendakian bukit yang dimulai ulang secara acak adalah algoritma yang sangat efektif dalam banyak kasus. Ternyata seringkali lebih baik menghabiskan waktu CPU menjelajahi ruang, daripada mengoptimalkan dengan hati-hati dari kondisi awal

Masalah

Maksimum lokal

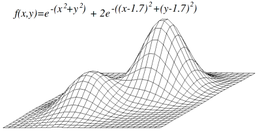
Sebuah permukaan dengan dua maxima lokal. (Hanya salah satunya adalah maksimum global.) Jika seorang pendaki bukit dimulai di lokasi yang buruk, mungkin menyatu ke maksimum yang lebih rendah.

Mendaki bukit tidak serta merta menemukan maksimum global, tetapi mungkin bertemu pada maksimum lokal. Masalah ini tidak terjadi jika heuristiknya cembung. Namun, karena banyak fungsi pendakian bukit yang tidak cembung mungkin sering gagal mencapai maksimum global. Algoritme pencarian lokal lainnya mencoba mengatasi masalah ini seperti pendakian bukit stokastik, jalan acak, dan anil simulasi.

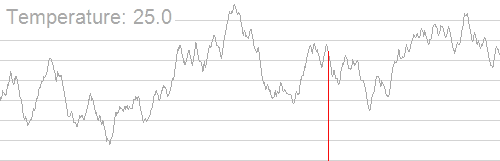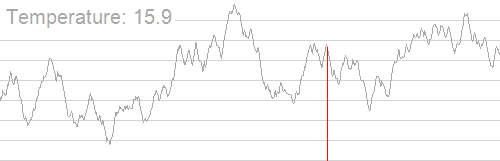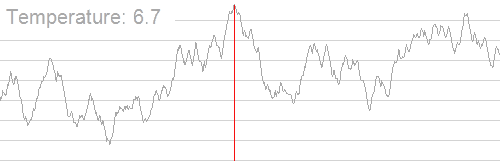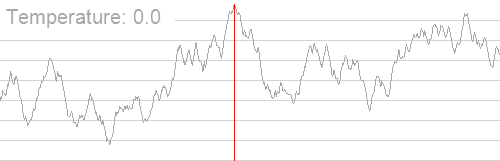
Meskipun banyak maxima lokal dalam grafik ini, maksimum global masih dapat ditemukan dengan menggunakan simulasi annealing. Sayangnya, penerapan simulasi anil adalah masalah khusus karena bergantung pada penemuan lompatan keberuntungan yang meningkatkan posisi. Dalam contoh ekstrem seperti itu, pendakian bukit kemungkinan besar akan menghasilkan maksimum lokal.

Pegunungan dan gang

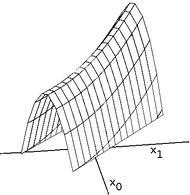
Sebuah punggungan

Punggungan adalah masalah yang menantang bagi pemanjat bukit yang mengoptimalkan dalam ruang terus menerus. Karena pemanjat bukit hanya menyesuaikan satu elemen dalam vektor pada satu waktu, setiap langkah akan bergerak dalam arah yang sejajar sumbu. Jika fungsi target membuat punggungan sempit yang menanjak ke arah yang tidak searah sumbu (atau jika tujuannya adalah meminimalkan, gang sempit yang menurun ke arah yang tidak searah sumbu), maka pemanjat bukit hanya dapat mendaki punggung bukit (atau menuruni gang) dengan zig-zag. Jika sisi punggung bukit (atau gang) sangat curam, maka pemanjat bukit mungkin terpaksa mengambil langkah yang sangat kecil karena zig-zag menuju posisi yang lebih baik. Dengan demikian, mungkin diperlukan waktu yang tidak masuk akal untuk naik ke punggung bukit (atau menuruni gang).

Sebaliknya, metode penurunan gradien dapat bergerak ke segala arah sehingga punggung bukit atau gang dapat naik atau turun. Oleh karena itu, penurunan gradien atau metode gradien konjugasi umumnya lebih disukai daripada mendaki bukit ketika fungsi target dapat dibedakan. Akan tetapi, pemanjat bukit memiliki keuntungan karena tidak memerlukan fungsi target yang dapat dibedakan, sehingga pemanjat bukit mungkin lebih disukai bila fungsi targetnya kompleks.

Dataran

Masalah lain yang terkadang terjadi dengan pendakian bukit adalah dataran tinggi. Dataran tinggi ditemui ketika ruang pencarian datar, atau cukup datar sehingga nilai yang dikembalikan oleh fungsi target tidak dapat dibedakan dari nilai yang dikembalikan untuk wilayah terdekat karena presisi yang digunakan oleh mesin untuk mewakili nilainya. Dalam kasus seperti itu, pemanjat bukit mungkin tidak dapat menentukan ke arah mana ia harus melangkah, dan mungkin mengembara ke arah yang tidak pernah mengarah pada perbaikan. 

Sumber Artikel: en.wikipedia.org

Pencarian Lokal Berulang (ILS) adalah istilah dalam matematika terapan dan ilmu komputer yang mendefinisikan modifikasi pencarian lokal atau metode mendaki bukit untuk memecahkan masalah optimasi diskrit.

Metode pencarian lokal bisa macet di minimum lokal, di mana tidak ada tetangga yang lebih baik yang tersedia.

Modifikasi sederhana terdiri dari panggilan iterasi ke rutin pencarian lokal, setiap kali dimulai dari konfigurasi awal yang berbeda. Ini disebut pencarian lokal berulang, dan menyiratkan bahwa pengetahuan yang diperoleh selama fase pencarian lokal sebelumnya tidak digunakan. Pembelajaran menyiratkan bahwa sejarah sebelumnya, misalnya memori tentang minima lokal yang ditemukan sebelumnya, ditambang untuk menghasilkan titik awal yang lebih baik dan lebih baik untuk pencarian lokal.

Asumsi implisitnya adalah distribusi berkerumun dari minima lokal: ketika meminimumkan suatu fungsi, menentukan minima lokal yang baik lebih mudah ketika memulai dari minimum lokal dengan nilai rendah daripada saat memulai dari titik acak. Satu-satunya peringatan adalah untuk menghindari kurungan di baskom atraksi tertentu, sehingga tendangan untuk mengubah peminim lokal menjadi titik awal untuk lari berikutnya harus cukup kuat, tetapi tidak terlalu kuat untuk menghindari kembali ke restart acak tanpa memori.

Pencarian Lokal Berulang didasarkan pada pembuatan urutan solusi optimal lokal dengan:

1. mengganggu minimum lokal saat ini;
2. menerapkan pencarian lokal setelah memulai dari solusi yang dimodifikasi.

Kekuatan gangguan harus cukup untuk mengarahkan lintasan ke cekungan tarikan yang berbeda yang mengarah ke optimum lokal yang berbeda.

Algoritma Gangguan

Algoritma gangguan untuk ILS bukanlah tugas yang mudah. Tujuan utamanya adalah untuk tidak terjebak dalam minimum lokal yang sama dan untuk mendapatkan properti ini benar, operasi undo dilarang. Meskipun demikian, permutasi yang baik harus mempertimbangkan banyak nilai, karena ada dua jenis permutasi buruk:

1. terlalu lemah: kembali ke minimum lokal yang sama
2. terlalu kuat: restart acak

Gangguan Tolok Ukur

Prosedurnya terdiri dari memperbaiki sejumlah nilai untuk gangguan sedemikian rupa sehingga nilai-nilai ini signifikan misalnya: pada probabilitas rata-rata dan tidak jarang. Setelah itu, pada saat runtime akan memungkinkan untuk memeriksa plot benchmark untuk mendapatkan ide rata-rata pada instance yang dilewati.

Gangguan Adaptif

Karena tidak ada fungsi apriori yang memberi tahu mana yang merupakan nilai yang paling cocok untuk gangguan tertentu, kriteria terbaik adalah membuatnya adaptif. Misalnya Battiti dan Protasi mengusulkan algoritma pencarian reaktif untuk MAX-SAT yang sangat cocok dengan kerangka kerja ILS. Mereka melakukan skema gangguan "terarah" yang diimplementasikan oleh algoritma pencarian tabu dan setelah setiap gangguan mereka menerapkan algoritma keturunan lokal standar. Cara lain untuk mengadaptasi gangguan adalah dengan mengubah secara deterministik kekuatannya selama pencarian.

Mengoptimalkan Gangguan

Prosedur lain adalah mengoptimalkan sub-bagian dari masalah, dengan mengaktifkan properti not-undo. Jika prosedur ini memungkinkan, semua solusi yang dihasilkan setelah gangguan cenderung sangat baik. Selanjutnya bagian-bagian baru juga dioptimalkan.

Kesimpulan

Metode ini telah diterapkan pada beberapa masalah optimasi kombinatorial termasuk masalah Penjadwalan Job Shop, Masalah Flow-Shop, Masalah Perutean Kendaraan serta banyak lainnya.

Sumber Artikel: en.wikipedia.org

Optimisasi

Optimasi atau optimasi matematis adalah proses pemilihan elemen terbaik dari sekumpulan elemen alternatif menurut kriteria tertentu. Masalah optimasi muncul di berbagai bidang ilmu pengetahuan, mulai dari ilmu komputer dan teknik hingga riset operasi dan ekonomi. Dalam bentuknya yang paling sederhana, masalah optimasi melibatkan upaya untuk memaksimalkan atau meminimalkan nilai suatu fungsi nyata dengan secara sistematis memilih masukan dari himpunan yang layak. Kajian optimasi dantekniknya telah menjadi bagian integral dari berbagai rumusan masalah di berbagai bidang matematika terapan.

Masalah Optimisasi

Dalam matematika, optimasi mengacu pada teori dan perhitungan titik ekstrem atau titik stasioner suatu fungsi. Masalah optimasi biasanya dinyatakan sebagai masalah minimalisasi, dimana kemungkinan solusi yang meminimalkan (atau memaksimalkan) nilai fungsi tujuan disebut solusi optimal. Banyak algoritma yang telah dikembangkan untuk menyelesaikan permasalahan nonkonveks, namun sebagian besar algoritma tersebut tidak dapat membedakan solusi optimal lokal dari solusi optimal global. Optimasi global adalah cabang matematika terapan dan analisis numerik yang mempelajari pengembangan algoritma deterministik dan memastikan konvergensi dalam waktu terbatas untuk menemukan solusi optimal terhadap masalah non-cembung. Notasi masalah optimasi seringkali dinyatakan melalui notasi khusus, dan terdapat berbagai metode optimasi, seperti: B. pemrograman linier dan metode iteratif berbasis perhitungan.

Notasi

Notasi dalam optimasi seringkali dinyatakan melalui notasi khusus. Notasi ini mungkin berbeda-beda tergantung pada jenis masalah pengoptimalan yang Anda hadapi. Misalnya pada optimasi program linier, notasi yang umum digunakan adalah notasi simpleks, sedangkan pada optimasi nonlinier, notasi yang umum digunakan adalah notasi turunan parsial. Ejaannya juga bisa berbeda-beda tergantung literatur atau sumber yang digunakan. Namun notasi khusus ini memudahkan untuk mengungkapkan masalah optimasisecara ringkas dan jelas.

Sejarah

Fermat, Lagrange, Newton dan Gauss mengembangkan rumus dan metode berulang untuk menemukan nilai optimal berdasarkan analisis. George B. Dantzig memperkenalkan istilah "pemrograman linier" untuk menyelesaikan beberapa kasus optimasi, mengikuti kontribusi sebelumnya oleh Leonid Kantorovich pada tahun 1939. Istilah "pemrograman" dalam konteks ini tidak mengacu pada "pemrograman komputer", tetapi pada penggunaan A.S. Program Angkatan Darat dalamproposal dan rencana pelatihan, topik yang menjadi fokus penelitian Dantzig. Dantzig menerbitkan algoritma Simplex pada tahun 1947, sementara John von Neumann mengembangkan teori dualitas. Peneliti terkenal di bidang optimasi antara lain Richard Bellman, Roger Fletcher, Ronald A. Howard, Fritz John dan banyak lainnya.

Disadur dari: https://id.wikipedia.org/wiki/Optimisasi

Komputasi Evolusioner

Dalam ilmu komputer, komputasi evolusioner adalah seperangkat algoritme pengoptimalan global yang terinspirasi oleh evolusi biologis dan subbidang kecerdasan buatan serta komputasi lunak yang mempelajari algoritme ini. Secara teknis, ini adalah rangkaian pemecah masalah coba-coba berbasis populasi dengan fungsi optimasi metaheuristik atau stokastik.

Dalam komputasi evolusioner, serangkaian solusi awal yang mungkin dihasilkan dan diperbarui secara berulang. Setiap generasi baru diciptakan dengan menghilangkan solusi yang kurang diinginkan secara stokastik, memperkenalkan perubahan kecil secara acak, dan, bergantung pada metodenya, mengacak informasi induknya. Dalam terminologi biologi, populasi solusi mengalami seleksi alam (atau seleksi buatan), mutasi, dan kemungkinan rekombinasi.Akibatnya, populasi secara bertahap akan berevolusi untuk meningkatkan kebugaran, dalam hal ini fungsi kebugaran yang dipilih dari algoritma.

Teknik komputasi evolusioner dapat memberikan solusi yang sangat optimal terhadap berbagai masalah, menjadikannya populer dalam ilmu komputer. Ada banyak varian dan ekstensi yang disesuaikan dengan masalah dan struktur data yang lebih spesifik. Evolusi komputasi juga terkadang digunakan dalam biologi evolusi sebagai metode eksperimental in silico untuk mempelajari aspek umum dari proses evolusi umum.

Sejarah

Konsep meniru proses evolusi untuk memecahkan masalah sudah ada sebelum munculnya komputer, misalnya ketika Alan Turing mengusulkan metode pencarian genetik pada tahun 1948. Mesin tipe B Turing menyerupai jaringan saraf primitif, dan hubungan antar neuron dipelajari melalui sejenis algoritma genetika. Mesin tipe P mereka menyerupai metode pembelajaran penguatan, di mana sinyal kesenangan dan rasa sakit menginstruksikan mesin untuk mempelajari perilaku tertentu. Meskipun makalah Turing baru diterbitkan pada tahun 1968 dan dia meninggal pada tahun 1954, karya-karya awal ini berdampak kecil pada perkembangan bidang komputasi evolusioner.

Komputasi evolusioner sebagai suatu bidang dimulai dengan sungguh-sungguh pada tahun 1950an dan 1960an.Pada tahun 1962, Lawrence J. Fogel mulai meneliti pemrograman evolusioner di Amerika Serikat, yang dianggap sebagai upaya kecerdasan buatan. Dalam sistem ini, mesin keadaan terbatas digunakan untuk menyelesaikan masalah prediksi: mesin ini akan bermutasi (menambah atau menghapus keadaan atau mengubah aturan transisi keadaan), dan mesin yang bermutasi lebih baik ini akan berkembang di generasi mendatang. Mesin keadaan terbatas terakhir dapat menghasilkanprediksi sesuai permintaan. Metode pemrograman evolusioner telah berhasil diterapkan pada masalah prediksi, identifikasi sistem, dan kontrol otomatis.Seiring waktu, ini telah diperluas untuk memproses data deret waktu dan pengembangan model strategi permainan.

Pada tahun 1964, Ingorechnerberg dan Hans-Paul Pelz memperkenalkan paradigma strategi evolusioner di Jerman. Karena teknik penurunan gradien tradisional menghasilkan hasil yang dapat terperangkap dalam nilai minimum lokal, Rechnerberg dan Pelz menyarankan bahwa mutasi acak (diterapkan pada semua parameter vektor solusi) dapat digunakan untuk menghindari nilai minimum ini. Solusi sekunder adalah hasil dari solusi primer, dan solusi yang paling berhasil dipertahankan untuk generasi mendatang.Teknik ini pertama kali digunakan oleh keduanya hingga berhasil memecahkan masalah optimasi dalam dinamika fluida. Awalnya, teknik optimasi ini dilakukan tanpa komputer, melainkan menggunakan dadu untuk menentukan mutasi acak.Jika metode sebelumnya hanya melacak satu organisme optimal dalam satu waktu (anak-anak bersaing dengan orang tuanya), algoritma genetika Holland melacak populasi besar (dengan banyak organisme bersaing di setiap generasi).

Pada tahun 1990-an, pendekatan baru terhadap komputasi evolusioner muncul, yang kemudian disebut pemrograman genetik, antara lain didukung oleh John Koza. Pada kelas algoritma ini, pokok bahasan evolusinya sendiri adalah program yang ditulis dalam bahasa pemrograman tingkat tinggi. Bagi Koza, programnya adalah ekspresi Lisp S, yang dapat dipandang sebagai pohon subekspresi. Representasi ini memungkinkan program untuk bertukar subpohon yang mewakili semacam campuran genetik.Program diberikan poin berdasarkan seberapa baik mereka melakukan tugas tertentu, dan poin ini digunakan untuk seleksi buatan. Induksi sekuens, pengenalan pola, dan perencanaan adalah penerapan paradigma pemrograman genetik yang berhasil.

Banyak tokoh lain yang berperan dalam sejarah komputasi evolusioner, meskipun karya mereka belum tentu cocok dengan salah satu cabang sejarah utama bidang ini. Simulasi komputer evolusi pertama yang menggunakan algoritma evolusi dan teknik kehidupan buatan dilakukan oleh Nils Aall Barricelli pada tahun 1953 dan hasil pertama dipublikasikan pada tahun 1954. Pelopor lain pada tahun 1950an adalah Alex Fraser, yang menerbitkan serangkaian artikel tentang simulasi kehidupan buatan. Pilihan.Seiring dengan meningkatnya minat akademis, peningkatan dramatis dalam kekuatan komputer memungkinkan penerapan praktis, termasuk pengembangan program komputer secara otomatis. Algoritme evolusioner sekarang digunakan untuk memecahkan masalah multidimensi dengan lebih efisien daripada perangkat lunak yang dibuat oleh perancang manusia dan juga untuk mengoptimalkan desain sistem.

Teknik

Teknik komputasi evolusioner mencakup berbagai algoritma optimasi metaheuristik yang digunakan untuk memecahkan masalah yang kompleks. Bidang ini mencakup pemodelan berbasis agen, optimasi koloni semut, sistem kekebalan buatan, kehidupan buatan (termasuk organisme digital), algoritma budaya, algoritma koevolusi, evolusi diferensial, evolusi multifase, algoritma estimasi distribusi, algoritma evolusi, pemrograman strategi evolusi dan evolusi, gen pemrograman ekspresi, algoritma genetika, pemrograman genetik, tata bahasa evolusioner, model evolusioner yang dapat dipelajari, sistem klasifikasi pembelajaran, algoritma memetika, neuroevolusi, optimalisasi kawanan partikel, pencarian antena kumbang, pengorganisasian mandiri sebagai peta yang diatur sendiri, pembelajaran kompetitif dan kecerdasan massa. Meskipun katalog ini berisi banyak algoritma yang diusulkan, penting untuk dicatat bahwa beberapa algoritma baru mungkin memiliki validasi eksperimental yang tidak memuaskan.Untuk informasi lebih lanjut tentang berbagai algoritma, lihat Bestiary of Evolutionary Computation.

Disadur dari : https://en.wikipedia.org/wiki/Evolutionary_computation

Analytic Hierarchy Process

Dalam teori pengambilan keputusan, proses hierarki analitik (AHP), juga disebut proses hierarki analitik, adalah teknik terstruktur untuk mengorganisir dan menganalisis keputusan yang kompleks, berdasarkan matematika dan psikologi. Dikembangkan oleh Thomas L. Saaty pada tahun 1970-an; Saaty bermitra dengan Ernest Forman untuk mengembangkan perangkat lunak Expert Choice pada tahun 1983, dan AHP telah dipelajari dan disempurnakan secara ekstensif sejak saat itu. AHP merupakan pendekatan yang akurat untuk mengukur bobot kriteria keputusan. Pengalaman para ahli individu digunakan untuk memperkirakan besaran relatif faktor melalui perbandingan berpasangan. Setiap responden membandingkan kepentingan relatif dari setiap pasangan item dengan menggunakan kuesioner yang dirancang khusus. Kepentingan relatif dari kriteria dapat ditentukan dengan bantuan AHP dengan membandingkan kriteria dan, jika ada, subkriteria secara berpasangan oleh para ahli atau pengambil keputusan. Atas dasar ini, alternatif terbaik dapat ditemukan. 

Penggunaan dan aplikasi 

AHP ditargetkan untuk pengambilan keputusan kelompok, dan digunakan untuk situasi keputusan, di bidang-bidang seperti pemerintahan, bisnis, industri, kesehatan dan pendidikan. 

Daripada memberikan keputusan yang "benar", AHP membantu para pengambil keputusan untuk menemukan keputusan yang paling sesuai dengan tujuan dan pemahaman mereka terhadap masalah. AHP menyediakan kerangka kerja yang komprehensif dan rasional untuk menyusun masalah keputusan, untuk merepresentasikan dan mengkuantifikasikan elemen-elemennya, untuk menghubungkan elemen-elemen tersebut dengan tujuan secara keseluruhan, dan untuk mengevaluasi solusi-solusi alternatif. 

Pengguna AHP pertama-tama menguraikan masalah keputusan mereka menjadi hirarki sub-masalah yang lebih mudah dipahami, yang masing-masing dapat dianalisis secara independen. Elemen-elemen hirarki dapat berhubungan dengan aspek apa pun dari masalah keputusan-berwujud atau tidak berwujud, diukur dengan cermat atau diperkirakan secara kasar, dipahami dengan baik atau kurang baik-apa pun yang berlaku untuk keputusan yang sedang dihadapi. 

Setelah hirarki dibuat, para pengambil keputusan mengevaluasi berbagai elemennya dengan membandingkan satu sama lain dua per satu, sehubungan dengan dampaknya terhadap elemen di atasnya dalam hirarki. Dalam membuat perbandingan, pengambil keputusan dapat menggunakan data konkret tentang elemen-elemen tersebut, dan mereka juga dapat menggunakan penilaian mereka tentang makna dan kepentingan relatif elemen-elemen tersebut. Penilaian manusia, dan bukan hanya informasi yang mendasarinya, dapat digunakan dalam melakukan evaluasi. 

AHP mengubah evaluasi ini menjadi nilai numerik yang dapat diproses dan dibandingkan di seluruh rentang masalah. Bobot atau prioritas numerik diturunkan untuk setiap elemen hirarki, sehingga memungkinkan elemen yang beragam dan sering kali tidak dapat dibandingkan satu sama lain dengan cara yang rasional dan konsisten. Kemampuan ini membedakan AHP dari teknik pengambilan keputusan lainnya. 

Pada langkah terakhir dari proses ini, prioritas numerik dihitung untuk setiap alternatif keputusan. Angka-angka ini mewakili kemampuan relatif alternatif untuk mencapai tujuan keputusan, sehingga memungkinkan pertimbangan langsung dari berbagai tindakan. 

Meskipun dapat digunakan oleh individu yang bekerja pada keputusan langsung, Proses Hirarki Analitik (AHP) paling berguna di mana tim orang bekerja pada masalah yang kompleks, terutama yang memiliki risiko tinggi, yang melibatkan persepsi dan penilaian manusia, yang resolusinya memiliki dampak jangka panjang. 

Situasi keputusan yang dapat diterapkan AHP meliputi: 

• Pilihan - Pemilihan satu alternatif dari sekumpulan alternatif yang mungkin yang memenuhi kriteria tertentu. Misalnya, memilih metode produksi baru yang paling efektif. 
• Prioritas - Pengalokasian sumber daya terbatas di antara berbagai proyek atau tujuan. Misalnya, menentukan alokasi anggaran untuk departemen yang berbeda. 
• Analisis Kerentanan - Identifikasi area yang paling rentan terhadap gangguan atau risiko. Misalnya, menilai kerentanan infrastruktur kota terhadap gempa bumi. 
• Estimasi - Menilai kemungkinan hasil berbagai keputusan. Misalnya, memperkirakan dampak kebijakan lingkungan pada perekonomian. 
• Konsensus - Membangun kesepakatan di antara sejumlah pihak dengan kepentingan yang berbeda. Misalnya, menemukan solusi yang dapat diterima bersama untuk masalah lingkungan yang kompleks. 
• Pemecahan Masalah - Memprioritaskan masalah yang perlu diselesaikan dan menemukan solusi terbaik untuk mereka. Misalnya, menentukan strategi untuk meningkatkan produktivitas di tempat kerja. 
• AHP dapat menjadi alat yang sangat berguna dalam situasi-situasi ini karena memungkinkan para pengambil keputusan untuk memperhitungkan berbagai faktor dan nilai yang berbeda, dan juga karena mendorong komunikasi dan konsensus di antara para anggota tim atau para pemangku kepentingan yang berbeda.

Disadur dari : en.wikipedia.org