Maximum dan Minimum
Dalam analisis matematis, maksimum dan minimum suatu fungsi mengacu pada nilai terbesar dan terkecil yang dapat diambil oleh fungsi tersebut. Nilai-nilai ini, yang biasa disebut sebagai nilai ekstrem, dapat didefinisikan dalam dua konteks: pertama, dalam rentang tertentu, yang dikenal sebagai nilai ekstrem lokal atau relatif, dan kedua, dalam seluruh rentang fungsi, yang dikenal sebagai nilai ekstrem global atau absolut. Konsep ini diperkenalkan dan dikembangkan oleh ahli matematika awal, dengan Pierre deFermat menjadi salah satu orang pertama yang mengusulkan teknik umum dan cukup untuk mencari nilai maksimum dan minimum dalam konteks fungsi matematika.
Dalam teori himpunan, maksimum dan minimum suatu himpunan mengacu pada elemen terbesar dan terkecil dari himpunan tersebut. Perlu diperhatikan bahwa himpunan tak hingga, seperti himpunan bilangan real, tidak memiliki nilai minimum dan maksimum karena tidak ada elemen yang membatasi nilai terbesar atau terkecil.Dalam statistika, terdapat konsep terkait yang disebut maksimum dan minimum sampling, yang mengacu pada nilai terbesar dan terkecil dalam suatu sampel data. Sebagai bagian integral dari analisis statistik, pemahaman maksimum dan minimum sangat penting untuk menilai distribusi data dan tren umum dalam suatu populasi.
Mencari Nilai Minimum dan Maximum
Menemukan maxima dan minima global adalah tujuan optimasi matematis. Jika suatu fungsi kontinu dalam interval tertutup, maka menurut teorema nilai ekstrim terdapat maksimum global dan minimum global. Selain itu, maksimum (atau minimum) global harus merupakan maksimum (atau minimum) lokal dalam domain atau pada batas domain. Jadi metode mencari maksimum (atau minimum) global adalah dengan mengamati semua maksimum (atau minimum) lokal di dalamnya sertamaksimum (atau minimum) dari titik-titik pada batas dan menemukan yang terbesar (atau lebih kecil).
Untuk fungsi terdiferensiasi, teorema Fermat menyatakan bahwa ekstrem lokal dalam suatu wilayah harus terjadi pada titik kritis (atau titik yang turunannya sama dengan nol). Namun, tidak semua titik balik bersifat ekstrem. Kita sering kali dapat membedakan apakah suatu titik kritis merupakan maksimum lokal, minimum lokal, atau bukan keduanya dengan menggunakan uji turunan pertama, uji turunan kedua, atau uji turunan orde tinggi, dengan memperhatikan diferensiasi yang cukup.
Untuk setiap fungsi yang ditentukan oleh bagian-bagian, nilai maksimum (atau minimum) dapat ditemukan dengan mencari nilai maksimum (atau minimum) dari masing-masing bagian secara terpisah dan kemudian menentukan mana yang terbesar (atau terkecil).
Fungsi Lebih dari satu Variabel
Kondisi serupa berlaku untuk fungsi dengan lebih dari satu variabel. Misalnya, pada gambar (yang dapat diperbesar) di sebelah kanan, kondisi yang diperlukan untuk maksimum lokal serupa dengan kondisi untuk fungsi variabel tunggal. Turunan parsial pertama dari z (variabel yang akan dimaksimalkan) adalah nol pada maksimumnya (titik terang di bagian atas gambar). Turunan parsial kedua bernilai negatif. Ini hanyalah kondisi yang diperlukan, namun tidak cukup untuk mencapai maksimum lokal sebesarkarena mungkin terdapat titik pelana.Agar kondisi ini dapat diselesaikan secara optimal, fungsi z juga harus terdiferensiasi sempurna. Uji turunan parsial kedua dapat membantu mengklasifikasikan titik tersebut sebagai maksimum relatif atau minimum relatif. Sebaliknya, terdapat perbedaan yang signifikan antara peran satu variabel dan peran beberapa variabel dalam mengidentifikasi kondisi ekstrem global. Misalnya, jika fungsi terdiferensiasi hingga f yang didefinisikan pada interval tertutup pada garis nyata mempunyai titik kritisyang merupakan minimum lokal, maka fungsi tersebut juga merupakan minimum global (gunakan teorema nilai antara dan teorema Rolle untuk membuktikannya) . dengan kontradiksi). Dalam dua dimensi atau lebih argumen ini gagal.Hal ini tercermin dari fungsinya.
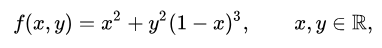
yang titik kritisnya hanya di (0,0), yang merupakan minimum lokal dengan f (0,0) = 0. Namun, tidak bisa menjadi minimum global, karena f (2,3) = −5.
Maxima atau minima dari suatu fungsi
Jika jangkauan suatu fungsi yang ekstremnya dicari terdiri dari fungsi itu sendiri (yaitu jika ekstrem suatu fungsi dapat ditemukan), maka ekstremnya ditemukan dengan kalkulus variasi.
Sehubungan dengan himpunan
Paragraf tersebut menjelaskan konsep maxima dan minima dalam konteks himpunan terurut. Jika suatu himpunan terurut S mempunyai m anggota terbesar, maka m disebut anggota maksimum himpunan tersebut, ditulis maks(S). Jika S adalah himpunan bagian dari himpunan terurut T dan m adalah elemen terbesar dari S dengan keteraturan karena T, maka m adalah batas atas terkecil dari S dalam T. Konsep serupa berlaku untuk elemen terkecil, elemen minimal, dan elemen terkecil. elemen bawah terbesar. melompat.
Fungsi maksimum dan minimum untuk himpunan digunakan dalam database dan dapat dihitung dengan cepat menggunakan partisi.Dalam pengurutan parsial umum, elemen terkecil dan elemen minimal tidak boleh tertukar. Dalam himpunan terurut sebagian (poset), elemen terbesar adalah batas atas himpunan, sedangkan elemen maksimum m dari sebuah poset A memenuhi m ≤ b untuk setiap b di A, dan jika m ≤ b maka m = b. Elemen terkecil atau terbesar dari sebuah poset adalah unik, tetapi sebuah poset dapat memiliki beberapa elemen minimum atau maksimum.
Dalam himpunan terurut lengkap, himpunan tersebut dapat mempunyai paling banyak satu elemen minimum dan satu elemen maksimum. Pada himpunan terurut sempurna, elemen minimum adalah elemen terkecil dan elemen maksimum adalah elemen terbesar.Jika rantainya berhingga, maka selalu mempunyai maksimum dan minimum. Jika rantainya tidak terbatas, maka tidak harus memiliki maksimum atau minimum. Misalnya himpunan bilangan asli tidak mempunyai nilai maksimum, namun mempunyai nilai minimum. Jika suatu rantai tak terhingga S dibatasi, penutupan Cl(S) dari himpunan tersebut dapat mempunyai minimum dan maksimum, yang disebut batas bawah terbesar dan batas atas terkecil dari S.
Disadur dari: en.wikipedia.org