Dalam pemrosesan sinyal, pengambilan sampel adalah reduksi sinyal waktu kontinu menjadi sinyal waktu diskrit. Contoh umum adalah mengubah gelombang suara menjadi rangkaian "sampel". Sampel adalah nilai suatu sinyal dalam waktu dan/atau ruang; definisi ini berbeda dari penggunaan istilah dalam statistik untuk merujuk pada sekumpulan nilai tersebut. [A] Sampler adalah subsistem atau fungsi yang mengekstraksi sampel dari sinyal kontinu. Sampler ideal teoritis menghasilkan sampel yang sesuai dengan nilai sesaat dari sinyal kontinu pada titik yang diinginkan. Sinyal asli dapat direkonstruksi dari rangkaian sampel hingga batas Nyquist dengan melewatkan urutan sampel melalui filter rekonstruksi.

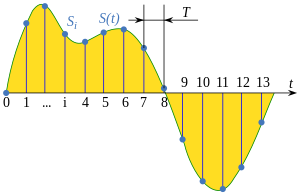
_{Signal sampling representation. The continuous signal S(t) is represented with a green colored line while the discrete samples are indicated by the blue vertical lines.}

Teori

Laju sampel atau laju sampel fs adalah jumlah rata-rata sampel yang diterima per detik, yaitu fs = 1/T, satuan sampel per detik, kadang disebut hertz, mis. 48kHz adalah 48.000 sampel per detik.

Rekonstruksi fungsi kontinu dari sampel dilakukan dengan menggunakan algoritma interpolasi. Rumus interpolasi Whittaker – Shannon secara matematis setara dengan filter low-pass ideal yang masukannya berupa rangkaian fungsi delta Dirac yang dimodulasi (dikalikan) dengan nilai sampel. Jika selang waktu antara sampel yang berdekatan adalah konstan (T), rangkaian fungsi delta disebut sisir Dirac. Secara matematis, sisir Dirac yang termodulasi sesuai dengan produk fungsi sisir dengan s(t). Abstraksi matematis ini kadang-kadang disebut pengambilan sampel impuls.

Kebanyakan sinyal sampel tidak direkam atau direkonstruksi. Akurasi rekonstruksi teoretis adalah ukuran umum efisiensi pengambilan sampel. Akurasi ini berkurang jika s(t) berisi komponen frekuensi dengan panjang siklus (periode) lebih kecil dari 2 interval pengambilan sampel (lihat Alias). Batas frekuensi ekuivalen dalam siklus per detik (hertz) adalah 0,5 siklus per sampel × fs sampel/detik = fs/2, yang dikenal sebagai laju pengambilan sampel Nyquist. Oleh karena itu, s(t) biasanya merupakan keluaran dari filter low-pass yang dikenal sebagai filter anti-aliasing. Tanpa filter antialiasing, frekuensi di atas frekuensi Nyquist mempengaruhi sampel dengan cara yang disalahartikan oleh proses interpolasi.

Pertimbangan praktis

Dalam praktiknya, sinyal kontinu diambil sampelnya menggunakan konverter analog-ke-digital (ADC), yang memiliki berbagai keterbatasan fisik. Hal ini menyebabkan penyimpangan dari rekonstruksi yang secara teoritis sempurna, yang secara kolektif dikenal sebagai distorsi.

Berbagai jenis distorsi dapat terjadi, termasuk:

• Aliasing. Sejumlah aliasing tidak dapat dihindari karena hanya fungsi teoretis yang panjangnya tak terhingga yang tidak dapat memiliki konten frekuensi di atas frekuensi Nyquist. Aliasing dapat dibuat sekecil apa pun dengan menggunakan filter anti-aliasing dalam jumlah yang cukup besar.
• Aperture dihasilkan dari fakta bahwa sampel diperoleh sebagai rata-rata waktu dalam wilayah pengambilan sampel, dan bukan hanya sama dengan nilai sinyal pada saat pengambilan sampel. Dalam rangkaian sampel dan penahan berbasis kapasitor, kesalahan bukaan disebabkan oleh berbagai mekanisme. Misalnya, kapasitor tidak dapat langsung melacak sinyal masukan dan kapasitor tidak dapat langsung diisolasi dari sinyal masukan.
• Jitter atau penyimpangan dari interval waktu sampel yang tepat.
• Noise, termasuk kebisingan sensor termal, kebisingan sirkuit analog, dll.
• Kesalahan batas laju perubahan tegangan, disebabkan oleh ketidakmampuan nilai masukan ADC berubah cukup cepat.
• Kuantisasi sebagai konsekuensi dari ketepatan terbatas kata-kata yang mewakili nilai yang dikonversi.
• Kesalahan karena efek non-linier lainnya dari pemetaan tegangan masukan ke nilai keluaran yang dikonversi (selain efek kuantisasi).

Meskipun penggunaan oversampling dapat sepenuhnya menghilangkan kesalahan apertur dan aliasing dengan memindahkannya keluar dari bandwidth, teknik ini tidak dapat digunakan dalam praktiknya di atas beberapa GHz dan bisa sangat mahal pada frekuensi yang jauh lebih rendah. Selain itu, meskipun pengambilan sampel berlebihan dapat mengurangi kesalahan kuantisasi dan nonlinier, hal ini tidak dapat sepenuhnya menghilangkannya. Oleh karena itu, ADC praktis pada frekuensi audio biasanya tidak menunjukkan aliasing, kesalahan aperture, dan tidak dibatasi oleh kesalahan kuantisasi. Sebaliknya, noise analog mendominasi. Pada frekuensi RF dan gelombang mikro, ketika oversampling tidak praktis dan filter mahal, kesalahan aperture, kesalahan kuantisasi, dan anti-aliasing dapat menjadi batasan yang signifikan.

Aplikasi

Audio digital menggunakan modulasi kode pulsa (PCM) dan sinyal digital untuk mereproduksi suara. Ini termasuk konversi analog-ke-digital (ADC), konversi digital-ke-analog (DAC), penyimpanan dan transmisi. Faktanya, sistem yang sering disebut sebagai digital sebenarnya adalah analog tingkat diskrit dan waktu diskrit dari analog listrik sebelumnya. Meskipun sistem modern bisa sangat rumit dalam metodenya, keuntungan utama sistem digital adalah kemampuannya untuk menyimpan, memperoleh, dan mengirimkan sinyal tanpa kehilangan kualitas.

Jika diperlukan untuk menangkap suara yang mencakup seluruh rentang pendengaran manusia 20-20.000 Hz, seperti saat merekam musik atau berbagai peristiwa akustik, bentuk gelombang audio biasanya ditangkap pada 44,1 kHz (CD), 48 kHz. , 88,2 kHz atau 96 kHz. Persyaratan kecepatan kira-kira dua kali lipat adalah konsekuensi dari teorema Nyquist. Kecepatan pengambilan sampel di atas 50kHz hingga 60kHz tidak dapat memberikan informasi yang lebih berguna bagi pendengar manusia. Produsen audio profesional awal memilih laju pengambilan sampel antara 40 dan 50 kHz karena alasan ini.

Disadur dari: https://en.wikipedia.org/wiki/Sampling_(signal_processing)

Sejarah antarmuka pengguna dapat dibagi menjadi beberapa fase berikut sesuai dengan jenis antarmuka pengguna yang dominan:

1945–1968: Antarmuka Pertama.

_{IBM 029}

Di era kuno, daya komputasi sangat langka dan mahal. Antarmuka pengguna masih belum sempurna. Pengguna harus beradaptasi dengan komputer dan bukan sebaliknya; antarmuka pengguna dianggap mubazir dan perangkat lunak dirancang untuk memaksimalkan pemanfaatan prosesor dengan overhead sesedikit mungkin.

Sisi masukan antarmuka mesin pengemas sebagian besar berupa kartu berlubang atau bahan serupa seperti pita kertas. Sisi pencetakan menambahkan printer linier ke materi ini. Selain operator sistem dan konsol, tidak ada interaksi manusia secara real-time dengan mesin pemukul.

Mengirimkan sejumlah pekerjaan ke mesin terlebih dahulu melibatkan pembuatan setumpuk kartu yang menjelaskan program dan kumpulan data. Kartu program tidak dilubangi oleh komputer itu sendiri, namun dengan penekanan tombol pada mesin khusus seperti mesin tik yang terkenal besar, tak kenal ampun, dan rentan terhadap kegagalan mekanis. Antarmuka perangkat lunak juga tidak kenal ampun, dengan sintaksis yang sangat ketat yang dirancang untuk mengurai sesedikit mungkin kompiler dan juru bahasa.

1969–sekarang: Antarmuka pengguna baris perintah.

_{Teletype Model 33 ASR}

Antarmuka baris perintah (CLI) berevolusi dari layar grup yang terhubung ke konsol sistem. Model interaksi mereka adalah rangkaian peristiwa permintaan-respons, di mana permintaan dinyatakan sebagai perintah teks dalam kosakata khusus. Waktu latensi jauh lebih rendah dibandingkan sistem batch, menurun dari hari atau jam menjadi detik. Dengan demikian, sistem baris perintah memungkinkan pengguna untuk mengubah pikirannya tentang tahapan selanjutnya dari suatu peristiwa sebagai respons terhadap umpan balik real-time atau hampir real-time tentang hasil sebelumnya. Perangkat lunak dapat bersifat eksploratif dan interaktif dengan cara yang tidak mungkin dilakukan sebelumnya. Namun, antarmuka tersebut terus memberikan beban memori yang relatif besar pada pengguna, sehingga memerlukan upaya serius dan waktu belajar untuk mengelolanya.

Sistem baris perintah paling awal menghubungkan teleprinter ke komputer, mengadaptasi teknologi matang yang telah terbukti efektif dalam mengirimkan informasi melalui kabel antar manusia. Teleprinter awalnya ditemukan sebagai perangkat transmisi dan penerimaan telegraf otomatis; sejarahnya dimulai pada tahun 1902, dan sejak tahun 1920-an mereka telah dibuat di kantor editorial dan di tempat lain. Daur ulang barang-barang tersebut tentu saja mempertimbangkan aspek ekonomi, namun psikologi dan peraturan yang paling tidak mengejutkan juga berperan; teleprinter menyediakan titik koneksi ke sistem yang familiar bagi banyak insinyur dan pengguna.

1985: Antarmuka pengguna SAA atau antarmuka pengguna berbasis teks.

_{DEC VT100 terminal}

Pada tahun 1985, dengan diperkenalkannya Windows dan antarmuka pengguna grafis lainnya, IBM menciptakan apa yang disebut standar Arsitektur Aplikasi Sistem (SAA), yang mencakup turunan dari Common User Access (CUA). CUA berhasil menciptakan apa yang kita kenal dan gunakan saat ini di Windows, dan merupakan standar yang digunakan oleh sebagian besar aplikasi konsol DOS atau Windows terbaru.

Hal ini menetapkan bahwa sistem dropdown harus berada di bagian atas layar, bilah status di bagian bawah, tombol harus tetap sama untuk semua fungsi umum (misalnya F2 - Terbuka akan berfungsi di semua aplikasi yang kompatibel dengan SAA). Hal ini berkontribusi besar terhadap kecepatan pengguna dalam mempelajari aplikasi, sehingga aplikasi ini dengan cepat menjadi populer dan menjadi standar industri.

Disadur dari: https://en.wikipedia.org/wiki/User_interface

Terlepas dari media transmisi fisik apa pun, jaringan dibangun dari blok bangunan sistem dasar tambahan, seperti pengontrol antarmuka jaringan, repeater, hub, jembatan, sakelar, router, modem, dan firewall. Peralatan tertentu sering kali berisi banyak blok penyusun sehingga dapat menjalankan banyak fungsi.

Network interfaces

Pengontrol antarmuka jaringan (NIC) adalah perangkat keras komputer yang menghubungkan komputer ke lingkungan jaringan dan memiliki kemampuan untuk memproses data jaringan tingkat rendah. Misalnya, NIC mungkin memiliki konektor untuk menghubungkan kabel atau antena untuk transmisi dan penerimaan nirkabel, dan sirkuit terkait.

Dalam jaringan Ethernet, setiap kartu jaringan memiliki alamat MAC (Media Access Control) unik, yang biasanya disimpan di pengontrol dan memori non-volatilnya. Untuk menghindari konflik alamat antar perangkat jaringan, keunikan alamat MAC dijaga dan dikelola oleh Institute of Electrical and Electronics Engineers (IEEE). Alamat MAC Ethernet panjangnya enam oktet. Tiga oktet paling signifikan dicadangkan untuk mengidentifikasi produsen kartu jaringan. Pabrikan tersebut, hanya menggunakan awalan yang ditetapkan, secara unik menetapkan tiga oktet paling tidak signifikan dari setiap antarmuka Ethernet yang mereka produksi.

Repeaters and hubs

Repeater adalah perangkat elektronik yang menerima sinyal jaringan, membersihkannya dari kebisingan yang tidak perlu, dan memulihkannya. Sinyal tersebut disiarkan ulang dengan daya yang lebih tinggi atau melewati rintangan sehingga sinyal dapat menempuh jarak yang lebih jauh tanpa degradasi. Sebagian besar konfigurasi twisted pair Ethernet memerlukan repeater untuk kabel yang panjangnya lebih dari 100 meter. Dalam kasus serat optik, repeater dapat ditempatkan pada jarak puluhan atau bahkan ratusan kilometer. Repeater bekerja pada lapisan fisik model OSI, namun masih memerlukan waktu untuk memulihkan sinyal. Hal ini dapat menyebabkan penundaan propagasi, yang mempengaruhi kinerja jaringan dan mempengaruhi pengoperasian yang benar. Akibatnya, banyak arsitektur jaringan membatasi jumlah repeater yang dapat digunakan pada jaringan, seperti aturan Ethernet 5-4-3. Repeater Ethernet multiport dikenal sebagai hub Ethernet. Selain memulihkan dan mendistribusikan sinyal jaringan, hub pengulang membantu mendeteksi tabrakan dan mengisolasi kegagalan jaringan. Hub dan repeater LAN sebagian besar sudah ketinggalan zaman karena adanya switch jaringan saat ini.

Bridges and switches

Jembatan jaringan dan switch jaringan berbeda dari hub karena mereka meneruskan frame hanya ke port yang terlibat dalam komunikasi, sementara hub terus meneruskan ke semua port. Bridge hanya memiliki dua port, namun switch dapat dianggap sebagai jembatan multi-port. Switch biasanya memiliki banyak port, memungkinkan topologi perangkat bintang dan switch tambahan secara seri.

Bridge dan switch beroperasi pada lapisan data (Layer 2) model OSI dan menjembatani lalu lintas antara dua atau lebih segmen jaringan untuk membentuk satu jaringan area lokal. Keduanya merupakan perangkat yang meneruskan frame data antar port berdasarkan alamat MAC setiap frame. Mereka belajar memetakan port fisik ke alamat MAC dengan memeriksa alamat sumber frame yang diterima dan meneruskan frame hanya jika diperlukan. Jika tujuannya adalah MAC tujuan yang tidak diketahui, perangkat mengirimkan kueri ke semua port kecuali sumber dan menemukan lokasinya dalam respons.

Bridge dan switch berbagi jaringan dan domain tabrakan, namun tetap mempertahankan satu domain siaran. Segmentasi jaringan menggunakan bridging dan switching membantu membagi jaringan besar yang padat menjadi sekelompok jaringan yang lebih kecil dan lebih efisien.

Routers

Router adalah perangkat jaringan yang meneruskan paket antar jaringan dengan memproses informasi alamat atau perutean yang terdapat dalam paket tersebut. Informasi perutean sering kali diproses bersama dengan tabel perutean. Sebuah router menggunakan tabel peruteannya sendiri untuk menentukan ke mana harus meneruskan paket dan tidak memerlukan penerusan paket, yang tidak efisien dalam jaringan yang sangat besar.

Modems

Modem (modulator-demodulator) digunakan untuk menghubungkan node jaringan dengan kabel yang awalnya tidak ditujukan untuk lalu lintas jaringan digital, atau secara nirkabel. Untuk melakukan hal ini, sinyal digital memodulasi satu atau lebih sinyal pembawa untuk menghasilkan sinyal analog yang dapat disesuaikan untuk memberikan karakteristik yang diperlukan untuk transmisi. Modem awal memodulasi sinyal audio yang dikirim melalui saluran telepon biasa. Modem masih umum digunakan pada saluran telepon yang menggunakan teknologi saluran pelanggan digital dan sistem televisi kabel yang menggunakan teknologi DOCSIS.

Firewalls

Firewall adalah perangkat jaringan atau perangkat lunak yang mengontrol keamanan jaringan dan aturan akses. Firewall ditempatkan pada koneksi antara jaringan internal yang aman dan jaringan eksternal yang berpotensi tidak aman seperti Internet. Firewall biasanya dikonfigurasi untuk menolak permintaan akses dari sumber yang tidak dikenal sambil mengizinkan operasi dari sumber yang teridentifikasi. Peran penting firewall dalam keamanan jaringan semakin meningkat seiring dengan meningkatnya serangan cyber.

Disadur dari: https://en.wikipedia.org/wiki/Computer_network

Tembaga adalah unsur kimia dengan lambang Cu (dari bahasa Latin: tembaga) dan nomor atom 29. Tembaga merupakan logam lunak, mudah dibentuk, dan mudah dibentuk dengan konduktivitas termal dan listrik yang sangat tinggi. Permukaan tembaga murni yang baru terekspos berwarna merah jambu-oranye. Tembaga digunakan sebagai konduktor panas dan listrik, sebagai bahan bangunan, dan sebagai komponen beberapa paduan logam, seperti perak yang digunakan dalam perhiasan, tembaga-nikel yang digunakan dalam peralatan kapal dan koin, dan digunakan secara konstan dalam pengukur regangan dan termokopel untuk mengukur suhu.

Tembaga adalah salah satu dari sedikit logam yang terdapat di alam dalam bentuk logam yang dapat langsung dimanfaatkan (logam asli). Hal ini menyebabkan penggunaan tembaga yang sangat awal di beberapa tempat, c. 8000 SM Ribuan tahun kemudian menjadi logam pertama yang dilebur dari bijih sulfida, c. 5000 SM; logam pertama yang dimasukkan ke dalam cetakan, sekitar 4000 SM; dan logam pertama sengaja dipadukan dengan logam lain, timah, untuk menghasilkan perunggu, c. 500 SM.

Pada zaman Romawi, tembaga ditambang terutama di Siprus, dimana nama logam tersebut berasal dari kata aes cyprium (logam Siprus), yang kemudian menjadi tembaga (Latin). Tembaga (Bahasa Inggris Kuno) dan Tembaga (Bahasa Inggris) berasal dari kata ini, ejaan selanjutnya pertama kali digunakan sekitar tahun 1530.

Senyawa yang umum mencakup garam tembaga(II), yang menghasilkan mineral seperti azurit, perunggu, sering kali berwarna biru atau hijau, dan pirus , dan secara luas dan historis digunakan sebagai pigmen. Tembaga yang digunakan pada bangunan, biasanya untuk atap, teroksidasi membentuk patina hijau dari senyawa yang disebut verdigris. Tembaga kadang-kadang digunakan dalam seni dekoratif baik sebagai unsur logam maupun sebagai pigmen dalam senyawa. Senyawa tembaga digunakan sebagai agen bakteriostatik, fungisida dan pengawet kayu.

Tembaga penting sebagai mineral makanan bagi semua organisme hidup karena merupakan komponen penting sitokrom c oksidase. Pada moluska dan krustasea, tembaga merupakan komponen pigmen darah hemosianin, yang pada ikan dan vertebrata lainnya digantikan oleh kompleks besi hemoglobin. Pada manusia, tembaga ditemukan terutama di hati, otot, dan tulang. Tubuh orang dewasa mengandung 1,4-2,1 mg tembaga per kilogram berat badan.

Disadur dari: https://id.wikipedia.org/wiki/Tembaga

Logam mulia biasanya dianggap sebagai logam sebagai elemen kimia yang biasanya tahan terhadap korosi dan biasanya terdapat di alam dalam bentuk mentah. Emas, platina, dan logam lain dari kelompok platina (rutenium, rhodium, paladium, osmium, iridium) paling sering diklasifikasikan seperti itu. Logam mulia terkadang termasuk perak, tembaga, dan merkuri, tetapi masing-masing biasanya muncul di alam bersama belerang, dalam bidang studi dan aplikasi khusus, jumlah elemen yang dianggap sebagai logam mulia bisa lebih kecil atau lebih besar. Dalam fisika, hanya ada tiga logam mulia: tembaga, perak, dan emas.

Dalam kedokteran gigi, perak tidak selalu dianggap sebagai logam mulia karena dapat mengalami korosi saat berada di dalam mulut. Dalam kimia, istilah logam mulia kadang-kadang digunakan secara lebih luas untuk merujuk pada unsur logam atau semi-logam apa pun yang tidak bereaksi dengan asam lemah dan tidak melepaskan gas hidrogen dalam prosesnya. Rangkaian yang lebih luas ini mencakup tembaga, merkuri, teknesium, renium, arsenik, antimon, bismut, polonium, emas, enam logam kelompok platina, dan perak.

Unsur Logam Mulia

Logam mulia terdiri dari rutenium (Ru), rodium (Rh), paladium (Pd), perak (Ag), osmium (Os), iridium (Ir), platina (Pt), dan emas (Au).

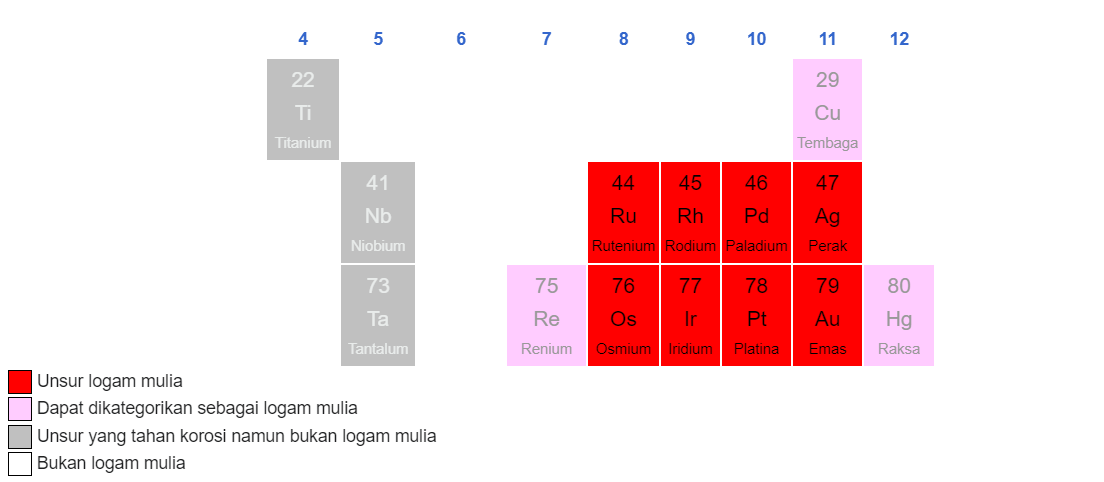
Disadur dari: https://id.wikipedia.org/wiki/Logam_mulia

Baja adalah paduan berbahan dasar besi. Besi murni kurang kuat dan mudah berkarat, namun memiliki daya tahan tinggi. Logam besi pada baja digabungkan dengan berbagai unsur lain, termasuk unsur karbon, untuk mengubah sifat-sifatnya. Beberapa logam yang biasa digunakan sebagai paduan adalah nikel, mangan, aluminium dan bismut. Unsur lain yang kurang umum adalah titanium, vanadium, kromium, tungsten, molibdenum, boron, dan niobium. Membandingkan material baja mempengaruhi karakteristik dan sifat dari baja itu sendiri.

Unsur karbon (C) biasanya ditambahkan pada baja untuk meningkatkan kekuatannya. Karbon dalam baja meningkatkan kekuatan baja, namun karbon juga mengurangi keuletan baja. Kandungan unsur karbon pada baja bervariasi antara 0,2-2,1% dari berat total. Kandungan karbon yang terlalu tinggi membuat baja menjadi rapuh atau mudah patah. Besi dapat membentuk dua bentuk kristal yaitu Body Center Cubic (BCC) dan Face Center Cubic (FCC), tergantung pada suhu penempaan. Pada susunan BCC, terdapat satu atom besi di tengah kubus atom, dan pada susunan FCC, terdapat satu atom besi pada setiap sisi dari enam sisi kubus atom. Interaksi alotropik antara logam besi dan unsur paduan seperti karbon memberikan sifat unik pada baja dan besi tuang.

Meskipun sebelumnya pandai besi memproduksi baja dalam tungku selama ribuan tahun, penggunaannya meningkat ketika metode produksi yang lebih efisien ditemukan pada abad ke-17. Dengan ditemukannya proses Bessemer pada pertengahan abad ke-19, baja diproduksi secara massal, sehingga biaya produksi menjadi lebih murah. Saat ini, baja adalah salah satu bahan yang paling banyak digunakan di dunia, dan produksi tahunannya menggantikan besi tempa sebanyak lebih dari 1,3 miliar ton. Baja merupakan komponen penting pada bangunan, infrastruktur, kapal, mobil, mesin, peralatan dan senjata. Baja modern umumnya dinilai menurut kualitasnya oleh beberapa badan standar. Proses pemurnian tingkat lanjut, seperti produksi baja oksigen dasar (BOS), menggantikan sebagian besar metode lama, sehingga mengurangi biaya produksi dan meningkatkan kualitas produk akhir.

Industri baja merupakan bagian penting dalam industrialisasi. Tanpa industri baja yang baik, industrialisasi tidak akan terjadi. Pentingnya industri baja dalam hal penggunaan baja dalam pembangunan infrastruktur, komponen mesin dan transportasi. Industri baja dapat menyerap banyak energi, selain itu industri baja memerlukan teknologi maju yang didukung oleh tenaga kerja terampil. Sepanjang sejarahnya, Uni Soviet memprioritaskan industri baja pada masa industrialisasi Uni Soviet pada tahun 1929 hingga 1941. Menurut statistik, China dan India merupakan 2 negara penghasil baja terbesar.

Definisi dan material

Kata baja dalam bahasa Inggris, yaitu baja, berasal dari kata keterangan Proto-Jerman stahlija atau stakhlijan (terbuat dari baja), yang berhubungan dengan stahlaz atau stahlija (padat tahan lama). Seperti yang telah dipelajari, kandungan karbon pada paduan baja adalah 0,002-2,14% berat campuran besi-karbon. Jumlah ini dapat bervariasi sesuai dengan unsur paduannya seperti mangan, kromium, nikel, besi, tungsten, karbon, dll. Pada dasarnya baja merupakan paduan besi-karbon yang tidak mengalami reaksi eutektik. Besi tuang, sebaliknya, mengalami reaksi ini. Jika kandungan karbon pada baja terlalu rendah, besi murni menjadi keras, lunak dan lemah dalam campurannya.

Kandungan karbon yang lebih tinggi pada baja biasa membentuk paduan yang sering disebut besi tuang. Meskipun besi yang berhasil digabungkan dengan karbon disebut baja karbon, baja paduan sendiri adalah baja yang dicampur dengan unsur lain untuk memberikan sifat tertentu pada baja. Unsur paduan yang umum meliputi: mangan, nikel, kromium, molibdenum, boron, titanium, vanadium, tungsten, kobalt, dan niobium. Unsur lain yang penting dalam pembuatan baja: Fosfor, belerang, silikon, dan sejumlah kecil oksigen, nitrogen, dan tembaga, yang biasanya tidak terdapat dalam baja.

Disadur dari: https://id.wikipedia.org/wiki/Baja