Analisis varians

Analisis varians (ANOVA) adalah kumpulan model statistik dan teknik estimasi yang berhubungan dengan analisis perbedaan antar rata-rata (yaitu, "perbedaan" antar kelompok). ANOVA dikembangkan oleh ahli statistik Ronald Fisher. ANOVA didasarkan pada hukum varians total, yang membagi varians yang terdapat pada suatu variabel menjadi komponen-komponen yang berasal dari sumber yang berbeda. Dalam bentuknya yang paling sederhana, ANOVA memberikan uji statistik apakah dua atau lebih rata-rata populasi adalah sama, sehingga memperluas uji-t melampaui dua rata-rata. Dengan kata lain, ANOVA digunakan untuk menguji perbedaan antara dua mean atau lebih.

Sejarah

Menurut Stigler, analisis diferensial efektif pada abad ke-20, namun asal usulnya sudah ada sejak berabad-abad yang lalu. Ini termasuk pengujian hipotesis, analisis kuadrat terkecil, metode pengujian, dan pengambilan sampel acak. Laplace menguji hipotesis ini pada tahun 1770. Sekitar tahun 1800, Laplace dan Gauss mengembangkan metode kuadrat terkecil untuk menggabungkan observasi, yang kemudian menyempurnakan metode yang digunakan dalam astronomi dan geografi. Hal ini juga mengawali banyak penelitian tentang kontribusi terhadap jumlah kuadrat.

Laplace tahu bagaimana memperkirakan varians dari jumlah kuadrat (bukan jumlah) dari residu. Pada tahun 1827, Laplace menggunakan metode kuadrat terkecil untuk memecahkan masalah analisis variabilitas pasang surut atmosfer yang diukur. Sebelum tahun 1800, para astronom mengisolasi kesalahan visual akibat waktu reaksi ("penulisan independen") dan mengembangkan metode untuk mengurangi kesalahan ini. Metode eksperimen yang digunakan dalam kajian persamaan personal kemudian diadopsi oleh bidang psikologi, yang mengembangkan metode eksperimen kuat (semua aspek) dengan penambahan pengacakan dan penyamaran. Penjelasan non-matematis tentang model efek aditif tersedia pada tahun 1885.

Istilah penyebaran diciptakan oleh Ronald Fisher dan diterbitkan dalam makalahnya pada tahun 1918 tentang genetika populasi teoretis, "Relatives to the Postulates of Mendelian Inheritance". Analisis formal disajikan dalam “Koreksi antara” Penerapan pertama analisis varians terhadap analisis data diterbitkan pada tahun 1921 dalam “Studi Variasi Produk I”. Perubahan deret waktu dibagi menjadi beberapa kategori yang menunjukkan faktor tahunan dan peluruhan lambat. Karya Fisher berikutnya, "Study of Crop Variation II", yang ditulis bekerja sama dengan Winifred Mackenzie dan diterbitkan pada tahun 1923, mempelajari variasi tanaman di petak yang ditanami varietas berbeda, berbeda, dan diberi pupuk berbeda. Analisis varians menjadi dikenal luas setelah diperkenalkan dalam buku Fisher tahun 1925 "Statistical Methods for Research Workers". Berbagai peneliti telah mengembangkan model kerentanan. Buku pertama diterbitkan dalam bahasa Polandia pada tahun 1923 oleh Jerzy Neyman.

Contoh

Analisis varians dapat digunakan untuk menggambarkan hubungan kompleks antar variabel, seperti paparan anjing. Pada pertunjukan anjing, distribusi bobot ras anjing yang berbeda sulit dilakukan. Katakanlah Anda ingin memprediksi berat badan anjing berdasarkan serangkaian karakteristik setiap anjing. Salah satu cara untuk melakukannya adalah dengan membagi populasi anjing ke dalam kelompok berdasarkan karakteristik tersebut.

Misalnya, kelompokkan anjing berdasarkan kombinasi dua pasang karakteristik: kecil hingga tua, berbulu pendek, dan berbulu panjang. Silakan pertimbangkan ini. Golongan tersebut adalah X₁, X2, dst. Jika klasifikasi ini berhasil, perbedaan berat badan anjing di setiap kelompok menjadi kecil, dan rata-rata antar kelompok. Namun, jika terdapat variasi besar dalam distribusi bobot dalam suatu kelompok dan rata-ratanya serupa, klasifikasi tidak akan berguna dalam menjelaskan perubahan bobot anjing.

Artinya, klasifikasi mengelompokkan anjing berdasarkan karakteristik seperti jenis hewan peliharaan dan jenis kegiatan. Orang yang lebih banyak berjudi dan mereka yang lebih banyak berjudi lebih mungkin untuk berhasil. Anjing yang paling serius berukuran besar, kuat, dan fungsional, tetapi anjing yang dipelihara sebagai hewan peliharaan berukuran lebih kecil dan ringan. Distribusi bobot anjing dalam klasifikasi ini mungkin memiliki variasi yang lebih sedikit dibandingkan dengan metode klasifikasi.

Namun, penghitungan bobot berdasarkan ras dapat meningkatkan klasifikasi. Semua Chihuahua ringan dan semua Saint Bernard berat. Perbedaan bobot antara preskriptor dan indikator belum tentu berbeda. Analisis varians dapat menjadi alat formal untuk memvalidasi kesimpulan tersebut, dan teknik ini digunakan dalam analisis data eksperimen atau dalam pengembangan model untuk menggambarkan hubungan antar variabel. Keuntungan dari metode ini mencakup kemampuan untuk menangani data non-numerik dan memberikan penilaian keyakinan terhadap hubungan yang teridentifikasi.

Kelas Model

Ada tiga kelas model yang digunakan dalam analisis varians, dan ini diuraikan di sini.

Model efek tetap

Model efek tetap (kelas I) dari analisis varians berlaku pada situasi di mana pelaku eksperimen menerapkan satu atau lebih perlakuan pada subjek eksperimen untuk melihat apakah nilai variabel respons berubah. Hal ini memungkinkan pelaku eksperimen memperkirakan kisaran nilai variabel respons yang akan dihasilkan oleh perlakuan tersebut dalam populasi secara keseluruhan.

Model efek acak

Model efek acak (kelas II) digunakan ketika perlakuan tidak tetap. Hal ini terjadi ketika berbagai tingkat faktor diambil sampelnya dari populasi yang lebih besar. Karena levelnya sendiri merupakan variabel acak, beberapa asumsi dan metode kontras perlakuan (generalisasi multivariabel dari perbedaan sederhana) berbeda dari model efek tetap.

Model efek campuran

Model efek campuran (kelas III) memuat faktor-faktor eksperimental baik jenis efek tetap maupun efek acak, dengan interpretasi dan analisis yang berbeda untuk kedua jenis tersebut.

Contoh

Eksperimen pengajaran dapat dilakukan oleh perguruan tinggi atau departemen universitas untuk menemukan buku teks pengantar yang baik, dengan setiap teks dianggap sebagai pengobatan. Model efek tetap akan membandingkan daftar teks kandidat. Model efek acak menentukan apakah terdapat perbedaan signifikan antara daftar item yang dipilih secara acak. Model efek campuran membandingkan teks saat ini (tetap) dengan alternatif yang dipilih secara acak.Mengidentifikasi efek tetap dan acak terbukti sulit karena banyaknya definisi yang bersaing.

Karateristik

ANOVA digunakan untuk menganalisis uji komparatif, yaitu pengujian yang menunjukkan perbedaan hasil. Signifikansi statistik dari pengujian tersebut ditentukan oleh rasio kedua perbedaan tersebut. Angka ini tidak tergantung pada kemungkinan perubahan observasi tes. Menambahkan lampiran ke semua tampilan tidak mengubah maknanya. Mengalikan seluruh pengamatan dengan suatu konstanta tidak mengubah maknanya. Oleh karena itu, signifikansi statistik dari hasil ANOVA tidak bergantung pada satuan yang digunakan untuk menyatakan observasi, termasuk persistensi dan kesalahan skala. Di era komputer, konstanta dari setiap observasi biasanya dihilangkan (mirip dengan menghilangkan angka sebelumnya) untuk menyederhanakan entri data. Ini adalah contoh pengkodean data.

Analisis Terkait

Analisis varians (ANOVA) adalah alat statistik yang digunakan untuk mengevaluasi perbedaan antara rata-rata dua kelompok atau lebih. Proses ini mencakup beberapa langkah penting yang mendukung desain dan implementasi percobaan, termasuk analisis hasil yang paling penting.

Saat mempersiapkan analisis varians, peneliti harus mempertimbangkan jumlah unit eksperimen yang dirancang untuk memenuhi tujuan eksperimen. Pengujian dilakukan beberapa kali, dengan pengujian pertama bertujuan untuk memperkirakan efek perlakuan dan mengukur kesalahan pengujian dengan cara yang tidak memihak. Analisis kekuatan juga digunakan untuk menilai kemungkinan keberhasilan dalam menolak hipotesis nol, dengan mempertimbangkan desain eksperimen, ukuran efek, dan tingkat signifikansi.

Ada tiga kelas model yang biasa digunakan dalam pengambilan sampel ANOVA. panggung Model efek tetap, model efek acak, model efek acak campuran. Model efek tetap digunakan ketika pelaku eksperimen memberikan perlakuan kepada subjek untuk mendeteksi perubahan variabel respon. Di sisi lain, model efek acak digunakan ketika tingkat faktor diambil sampelnya dari populasi yang lebih besar. Model efek campuran mencakup dua jenis kondisi eksperimental: efek tetap dan efek acak.

Setelah model ditentukan, analisis ANOVA terdiri dari membandingkan mean dan varians serta rasio odds yang memenuhi ambang batas signifikansi. Jika tercapai maka hasilnya akan signifikan. Penghitungan efek pengobatan dilakukan dengan memperkirakan efek masing-masing perlakuan dengan selisih antara rata-rata observasi yang diberikan perlakuan dan rata-rata keseluruhan. Pengujian lanjutan dilakukan setelah ditemukan efek signifikan di ANOVA, seperti pengujian berpasangan atau perbandingan ganda.

Langkah terakhir adalah validasi model dan analisis lebih lanjut. Pengujian dilakukan untuk memastikan asumsi ANOVA tidak dilanggar, homoskedastisitas dan normalitas residu diperiksa. Berdasarkan hasil pengujian yang telah dilakukan sebelumnya, dilakukan analisis persiapan untuk menyesuaikan desain pengujian selanjutnya. Mengetahui langkah-langkah ini memungkinkan peneliti untuk melakukan dan menafsirkan ANOVA dalam kerangka penelitian statistik.

Disadur dari : en.wikipedia.org

Uji Chi-Kuadrat

Uji chi-kuadrat (juga uji chi-kuadrat atau χ2) adalah uji hipotesis statistik yang digunakan dalam analisis tabel kontingensi ketika ukuran sampel besar. Secara sederhana, uji ini terutama digunakan untuk memeriksa apakah dua variabel kategorikal (dua dimensi dari tabel kontingensi) bersifat independen dalam mempengaruhi statistik uji (nilai dalam tabel).Uji ini valid jika statistik uji terdistribusi secara chi-kuadrat di bawah hipotesis nol, khususnya uji chi-kuadrat Pearson dan varian-variannya. Uji chi-kuadrat Pearson digunakan untuk menentukan apakah ada perbedaan yang signifikan secara statistik antara frekuensi yang diharapkan dan frekuensi yang diamati dalam satu atau lebih kategori tabel kontingensi. Untuk tabel kontingensi dengan ukuran sampel yang lebih kecil, uji eksak Fisher digunakan sebagai gantinya.

Dalam aplikasi standar uji ini, pengamatan diklasifikasikan ke dalam kelas-kelas yang saling terpisah. Jika hipotesis nol yang menyatakan bahwa tidak ada perbedaan antara kelas-kelas dalam populasi adalah benar, maka statistik uji yang dihitung dari pengamatan mengikuti distribusi frekuensi χ2. Tujuan dari pengujian ini adalah untuk mengevaluasi seberapa besar kemungkinan frekuensi yang diamati dengan asumsi hipotesis nol benar.

Statistik uji yang mengikuti distribusi χ2 terjadi ketika observasi bersifat independen. Ada juga uji χ2 untuk menguji hipotesis nol independensi dari sepasang variabel acak berdasarkan pengamatan terhadap pasangan tersebut.

Uji chi-kuadrat sering kali merujuk pada uji yang distribusi statistik uji mendekati distribusi χ2 secara asimtotik, yang berarti bahwa distribusi sampling (jika hipotesis nol benar) dari statistik uji mendekati distribusi chi-kuadrat semakin mendekati distribusi chi-kuadrat seiring dengan bertambahnya jumlah sampel.

Sejarah

Pada abad ke-19, metode analisis statistik terutama diterapkan dalam analisis data biologis dan merupakan kebiasaan bagi para peneliti untuk mengasumsikan bahwa pengamatan mengikuti distribusi normal, seperti Sir George Airy dan Mansfield Merriman, yang karyanya dikritik oleh Karl Pearson dalam makalahnya pada tahun 1900.

Pada akhir abad ke-19, Pearson menyadari adanya kemencengan yang signifikan dalam beberapa pengamatan biologis. Untuk memodelkan pengamatan terlepas dari normal atau miring, Pearson, dalam serangkaian artikel yang diterbitkan dari tahun 1893 hingga 1916, merancang distribusi Pearson, keluarga distribusi probabilitas kontinu, yang mencakup distribusi normal dan banyak distribusi miring, dan mengusulkan metode analisis statistik yang terdiri dari penggunaan distribusi Pearson untuk memodelkan pengamatan dan melakukan uji kecocokan (test of goodness of fit) untuk menentukan seberapa baik model tersebut benar-benar sesuai dengan pengamatan.

Uji Chi-Kuadrat Pearson

Pada tahun 1900, Pearson menerbitkan sebuah makalah tentang uji χ2 yang dianggap sebagai salah satu fondasi statistik modern. Dalam makalah ini, Pearson menginvestigasi uji kecocokan (goodness of fit).

Misalkan n pengamatan dalam sampel acak dari sebuah populasi diklasifikasikan ke dalam k kelas yang saling terpisah dengan masing-masing jumlah pengamatan xi (untuk i = 1,2,...,k), dan hipotesis nol memberikan probabilitas pi bahwa sebuah pengamatan masuk ke dalam kelas ke-i. Jadi kita memiliki angka yang diharapkan mi = npi untuk semua i, di mana :

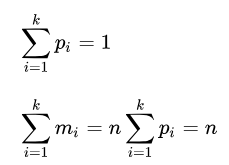
Pearson berasumsi bahwa, dalam situasi di mana hipotesis nol benar, n → tidak terbatas, maka distribusi batas bawah adalah distribusi χ2.

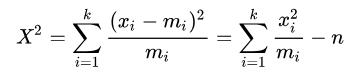
Pearson pertama kali menyatakan kasus bahwa angka yang diharapkan adalah angka besar yang diketahui semua sel, dengan asumsi bahwa setiap pengamatan. χ 2 dan k − 1 derajat kebebasan.Namun, Pearson mempertimbangkan kasus di mana nilai yang diharapkan bergantung pada parameter yang ditentukan dalam model dan berasumsi bahwa indikator m i bilangan real dan m: ' I adalah bilangan yang diharapkan, yang mana berbeda.

Pearson pertama kali membahas kasus bahwa angka yang diharapkan (mi) adalah angka kritis yang diketahui semua sel, dengan asumsi bahwa setiap pengamatan (xi) dapat didistribusikan secara acak, dan ketika n, kita sampai pada hasil X^2 ​​di wilayah tersebut. Ini mengikuti distribusi chi-kuadrat dengan derajat kebebasan (k - 1).Namun, Pearson mempertimbangkan kasus di mana angka yang diharapkan di masa depan bergantung pada parameter yang ditentukan dalam contoh dan alasan, menggunakan notasi mi: angka dan m ' Saya adalah perkiraannya, perbedaannya.

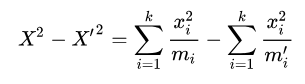
Biasanya, kesalahan perkiraan ini akan positif dan cukup kecil untuk dihilangkan. Sebagai kesimpulan, Pearson berpendapat bahwa jika kita menganggap (X'^2) juga terdistribusi sebagai distribusi chi-kuadrat dengan (k - 1) derajat kebebasan, kesalahan dalam perkiraan ini tidak akan mempengaruhi keputusan praktis. Kesimpulan ini menimbulkan beberapa kontroversi dalam penerapan praktisnya dan baru diselesaikan selama 20 tahun hingga makalah Fisher tahun 1922 dan 1924.

Contoh lain dari uji Chi-kuadrat

Contoh lain dari uji chi-kuadrat adalah penggunaannya untuk memeriksa apakah varians suatu populasi yang berdistribusi normal mempunyai nilai tertentu berdasarkan varians sampel. Meskipun pengujian ini jarang dilakukan dalam praktiknya karena varians populasi tidak diketahui, ada beberapa statistik yang dapat digunakan untuk memperkirakan distribusi chi-kuadrat resmi.

Contohnya adalah uji eksak Fisher. Untuk menguji kemandirian, kami melakukan uji chi - 2 × 2. Terdapat juga uji binomial yang dapat digunakan sebagai alternatif uji chi-kuadrat 2 × 1 untuk menentukan goodness of fit.Beberapa uji chi lainnya persegi uji chi-kuadrat Cochran-Mantel-Haenszel digunakan. Uji kuadrat, uji McNemar digunakan untuk beberapa tabel berpasangan 2×2, uji korelasi Tukey dan uji Portmanteau dalam analisis deret waktu untuk menguji autokorelasi. Selain itu, uji rasio kemungkinan dalam pemodelan statistik digunakan untuk menguji apakah akan berpindah dari model sederhana ke model yang lebih kompleks yang berisi model sederhana.

Disadur dari: en.wikipedia.org

Bagan Kendali

Peta kendali adalah desain grafis yang digunakan dalam pengendalian produksi untuk menentukan apakah kualitas dan proses produksi dikontrol secara stabil. Pengendalian waktu disusun dalam grafik, dan variabel dievaluasi berdasarkan perbedaan data dari kondisi saat ini atau di luar batas kendali. Diagram kendali diklasifikasikan sebagai Diagram Kontrol Individual Shewhart (ISO 7870-2) dan CUSUM (atau Diagram Kontrol Kumulatif Kumulatif) (ISO 7870-4).

Diagram kontrol, juga dikenal sebagai Diagram Shewhart (setelah Walter A. ). Shewhart) bagan perilaku proses adalah alat kendali statistik yang digunakan untuk menentukan apakah suatu proses manufaktur atau bisnis terkendali. Lebih tepatnya, peta kendali adalah alat grafis untuk pemantauan proses statistik (SPM). Kebanyakan diagram kendali tradisional dirancang untuk memantau parameter proses ketika bentuk dasar distribusi proses diketahui. Namun, di abad ke-21, tersedia teknik yang lebih canggih untuk mengontrol aliran data yang masuk tanpa mengetahui distribusi prosesnya. Rencana energi yang tidak terdistribusi menjadi semakin populer.

Gambaran Umum

Jika analisis peta kendali menunjukkan bahwa proses saat ini berada dalam kendali (yaitu stabil, dengan variasi dari sumber yang umum pada proses), tidak diperlukan perubahan atau perubahan pada parameter kendali. Data proses juga dapat digunakan untuk memprediksi kinerja masa depan. Jika grafik menunjukkan bahwa tidak ada kontrol, analisis Anda dapat menentukan penyebab variasi tersebut. Hal ini karena kinerja proses menurun. Proses yang stabil tetapi beroperasi di luar batas yang diinginkan (ditentukan) (misalnya tingkat keseimbangan berada dalam kendali statistik tetapi mungkin melebihi batas yang diinginkan) Kemampuan untuk memahami masalah kinerja saat ini dan meningkatkan kinerja proses.

Rencana operasi adalah salah satu dari tujuh alat kontrol kualitas dasar. Plot daya digunakan untuk data deret waktu, juga dikenal sebagai data kontinu atau variabel. Ini juga dapat digunakan untuk data yang sangat mirip (yaitu ketika Anda ingin membandingkan sampel yang diambil pada waktu yang sama atau hasil karya orang yang berbeda). Namun, Anda harus mempertimbangkan jenis grafik yang digunakan untuk melakukan hal ini.

Sejarah

Walter A. Shewhart, yang bekerja di Bell Laboratories pada tahun 1920-an, mengembangkan rencana operasional. Insinyur perusahaan bekerja untuk meningkatkan keandalan sistem telekomunikasi. Penguatan dan peralatan lainnya harus dikubur di bawah tanah, yang membuat bisnis lebih efisien untuk mengurangi jumlah kerusakan dan perbaikan. Pada tahun 1920-an, para insinyur menyadari pentingnya mengurangi variasi produksi. Kami juga menyadari bahwa perubahan proses karena ketidaksesuaian meningkatkan variabilitas dan menurunkan kualitas.

Shewhart membingkai masalah ini dalam kaitannya dengan penyebab umum dan spesifik ketidaksetaraan, dan pada tanggal 16 Mei 1924, dia menulis memo internal yang menguraikan bagan organisasi sebagai cara untuk menguraikannya. Bos Shewhart, George Edwards, mengenang: "Dr. Shewhart menyiapkan catatan singkat tentang sebuah halaman. Sekitar sepertiga halaman dikhususkan untuk desain sederhana yang sekarang kita kenal sebagai desain, dan yang sekarang kita kenal sebagai kendali mutu. Itu secara sederhana menggambarkan semua prinsip dan konsep penting yang terlibat dalam keberadaan." Shewhart menekankan bahwa proses produksi perlu dibawa ke kondisi kendali statistik dan variasi faktor yang acak, dan menjaganya tetap terkendali, guna memprediksi kinerja masa depan dan mengendalikan proses secara ekonomis.

Shewhart meletakkan fondasinya untuk kontrol. Bagan dan konsep dikontrol secara statistik melalui eksperimen yang dirancang dengan cermat. Meskipun Shewhart berpegang pada teori matematika statistik, ia mengakui bahwa data dari proses fisik menghasilkan "distribusi normal" (distribusi Gaussian, juga dikenal sebagai "kurva panah"). Ia menemukan bahwa perbedaan yang diamati pada data produksi tidak sama dengan data alam (pergerakan partikel Brown). Shewhart menyimpulkan bahwa meskipun semua proses berbeda, beberapa proses menunjukkan perbedaan makna pekerjaan, sedangkan proses lainnya menunjukkan perbedaan yang tidak ditemukan dalam sistem sebab akibat dari proses tersebut.Pada tahun 1924 atau 1925, Shewhart menangkap inovasi tersebut.

Hal ini menarik perhatian W. Edwards Deming, yang saat itu bekerja di Hawthorne House. Deming kemudian bekerja untuk Departemen Pertanian Amerika Serikat, di mana dia menjadi konsultan matematika di Amerika Serikat. Biro Sensus. Setengah abad kemudian, Deming menjadi pemimpin dan mentor yang hebat dalam karya Shewhart. Setelah kekalahan Jepang pada akhir Perang Dunia II, Deming menjabat sebagai penasihat statistik Panglima Tertinggi Angkatan Darat. Melalui keterlibatannya di Jepang dan bertahun-tahun sebagai konsultan industri di sana, gagasan Shewhart dan penggunaan rencana manajemen menyebar ke seluruh manufaktur Jepang selama tahun 1950an dan 1960an.Bonnie Small, bekerja di Allentown Setelah pembangunan transistor 1950 ' S. pabrik Meningkatkan kinerja pabrik dalam pengendalian kualitas menggunakan metode Shewhart dan pembuatan hingga 5000 rencana pengendalian. Pada tahun 1958, bukunya, 『Western Electric Statistics Quality Control Manual』 diterbitkan dan digunakan di AT&T.

Detail Bagan

Peta kendali adalah alat statistik yang berisi indikator-indikator yang mewakili pengukuran statistik karakteristik kualitas sampel yang diambil dari proses pada waktu yang berbeda. Disebut juga data. Rata-rata atau median statistik dihitung menggunakan semua sampel dan garis median ditarik pada rata-rata atau median tersebut. Selain itu, deviasi standar statistik dihitung menggunakan seluruh sampel atau untuk periode referensi tertentu yang dapat digunakan untuk menilai perubahan. Batas kendali atas dan bawah juga dikenal sebagai "batas proses alami" dan mewakili ambang batas di mana efek proses dianggap "tidak dapat diterima", biasanya 3 standar deviasi dari garis tengah.

Grafik kekuatan memiliki fitur lain, mungkin Hal ini mencakup peringatan atau batas kendali yang lebih ketat, zonasi, dan dokumentasi kejadian terkait ketika insinyur kualitas bertanggung jawab atas kualitas proses. Grafik juga dapat mencakup fitur untuk alasan tertentu dan aturan pencarian sinyal, seperti area di luar kendali, rangkaian tujuh sinyal, pergerakan di atas atau di bawah tujuh poin. Aturan-aturan ini akan membantu Anda mendeteksi perubahan signifikan dalam proses Anda dan memandu tindakan perbaikan.

Penggunaan Grafik

Jika proses dikendalikan dengan statistik proses, 99,7300% dari seluruh titik akan berada dalam batas kendali. Pengamatan yang berada di luar batas, atau pola sistematis di dalamnya, menunjukkan munculnya sumber variasi baru (dan tidak terduga), yang dikenal sebagai variasi penyebab spesifik. Bagan kendali yang "menunjukkan" adanya masalah tertentu harus segera diselidiki, karena peningkatan variabilitas akan meningkatkan biaya kualitas.

Ini akan membantu memantau area pengambilan keputusan penting. Domain kontrol memberikan informasi tentang perilaku proses tanpa hubungan intrinsik apa pun dengan tujuan desain atau spesifikasi teknis. Dalam praktiknya, rata-rata proses (dan garis dasar) mungkin tidak sesuai dengan nilai (dan target) karakteristik kualitas yang ditentukan karena desain proses mungkin tidak memberikan tingkat karakteristik proses yang diinginkan.

Batas atau target diagram kendali terbatas . Dalam praktiknya, praktik yang paling efektif adalah dengan meminimalkan variasi proses, namun orang yang terlibat dalam proses tersebut (misalnya insinyur mesin) mungkin tertarik pada proses sesuai dengan kebutuhan. Mencoba menciptakan suatu proses di mana pusat lingkungan tidak sesuai dengan kegiatan yang direncanakan sesuai dengan persyaratan yang ditetapkan akan meningkatkan variabilitas proses, meningkatkan biaya secara signifikan, dan banyak inefisiensi administratif.

Namun, studi dinamika proses menguji hubungan antara batas proses alami (batas kendali) dan persyaratan.Tujuan bagan kendali adalah untuk memberikan cara mudah untuk mengidentifikasi peristiwa, yang mengindikasikan peningkatan perubahan proses. Keputusan sederhana ini bisa menjadi sulit ketika keadaan proses terus berubah. Bagan kekuatan memberikan dasar statistik untuk perubahan. Ketika perubahan diidentifikasi dan dianggap positif, alasannya harus diidentifikasi dan cara kerja yang baru harus diidentifikasi. Jika perubahan yang dilakukan salah, penyebabnya harus diidentifikasi dan dihilangkan.

Tujuan penambahan zona peringatan atau membagi peta kendali menjadi beberapa zona adalah untuk memberikan peringatan dini jika terjadi masalah. Daripada segera memulai proses perbaikan proses untuk menentukan apakah ada masalah tertentu, insinyur kualitas dapat meningkatkan laju pengambilan sampel produk proses untuk sementara sampai jelas bahwa proses terkendali. Dengan menggunakan batasan 3-sigma, sebuah sinyal muncul kurang dari satu kali dalam 22 sinyal untuk proses putaran, dan kira-kira satu dalam 370 (1/370.4) sinyal untuk proses distribusi normal. Tingkat peringatan 2-sigma dicapai kira-kira sekali setiap 22 (1/21.98) titik yang ditemukan pada data berdistribusi normal. (Misalnya, mean sampel terbesar dari sebagian besar distribusi yang mendasarinya adalah variabel yang didistribusikan menurut kebijakan batas pusat).

Walter A. Shewhart menetapkan batas 3-sigma (ukuran 3 standar) dengan beberapa referensi dasar: Pertama, didasarkan pada hasil perkiraan pertidaksamaan Chebyshev, yang menyatakan bahwa probabilitas deviasi k deviasi standar dari mean adalah sebagai maksimum 1/k^2. Shewhart kemudian menyatakan ketidaksetaraan Vysochanskii-Petunin, yang berlaku pada distribusi probabilitas unimodal, dan menyatakan bahwa probabilitas hasil lebih besar dari k deviasi standar dari mean adalah 4/(9k ^2).\ nJuga, sangat umum dalam distribusi normal.

Diketahui bahwa 99,7% observasi terjadi dalam 3 pengukuran mean yang berbeda. Shewhart merangkum pemikirannya dengan mengatakan bahwa pembenaran kriteria batas 3-Sigma harus berasal dari bukti empiris bahwa pendekatan tersebut berhasil. Meskipun awalnya dia menguji pembatasan distribusi probabilitas, Shewhart akhirnya menyimpulkan bahwa semua harapan untuk menemukan bentuk fungsional unik untuk f telah gagal. : Teorema Neyman-Pearson. Menurut Deming, di sebagian besar situasi industri, ketidakpastian populasi dan kerangka sampel menyulitkan penggunaan metode statistik tradisional. Demikian berpendapat bahwa ketiga ambang batas memberikan panduan praktis dan ekonomis untuk dua jenis kesalahan: mengatribusikan varians ke penyebab spesifik yang merupakan bagian dari sistem (kesalahan Tipe I) dan mengatribusikan varians ke penyebab spesifik (kesalahan Tipe I) ke penyebab umum. Faktanya, penyebabnya adalah faktor independen (kesalahan tipe II).

Saat menghitung batas kendali, deviasi standar yang diperlukan adalah varians dalam proses dari penyebabnya. Oleh karena itu, penduga umum seperti model varians tidak digunakan karena memperkirakan jumlah kesalahan kuadrat yang hilang dari faktor persekutuan dan varians dari faktor independen. Anda dapat menggunakan metode yang menggunakan rasio interval sampel terhadap deviasi standar. Dampaknya lebih kecil terhadap pengamatan kritis yang mengindikasikan permasalahan tertentu.

Disadur dari: en.wikipedia.org

Korelasi

Dalam statistik, korelasi atau ketergantungan mengacu pada hubungan statistik antara dua variabel acak atau data bivariat, baik kausal atau tidak. Khususnya dalam konteks statistik, istilah "korelasi" sering kali mengacu pada derajat hubungan linier antara sepasang variabel. Contoh fenomena dependen adalah hubungan antara tinggi badan orang tua dan keturunannya, serta hubungan antara harga suatu barang dan jumlah yang dibeli oleh konsumen, seperti yang ditunjukkan pada kurva permintaan.

Korelasi berguna karena dapat menunjukkan prediksi. hubungan yang dapat digunakan dalam praktek. Misalnya, sebuah perusahaan utilitas mungkin menghasilkan lebih sedikit listrik pada siang hari berdasarkan korelasi antara permintaan listrik dan cuaca. Dalam situasi ini terdapat hubungan sebab akibat dimana kondisi cuaca ekstrim memaksa masyarakat untuk menggunakan lebih banyak listrik untuk pemanas atau pendingin. Pada saat yang sama, perlu dicatat bahwa keberadaan korelasi tidak cukup untuk menyimpulkan adanya hubungan sebab akibat, karena korelasi tidak selalu menunjukkan hubungan sebab akibat.

Secara formal, korelasi dianggap sebagai variabel acak. bergantung jika tidak memenuhi sifat matematis dari kemungkinan independensi. Dalam istilah teknis, korelasi dapat merujuk pada berbagai operasi matematika spesifik antara variabel yang diuji dan nilai yang diharapkan terkait. Beberapa koefisien korelasi yang umum digunakan, seperti koefisien korelasi Pearson (sering dilambangkan dengan ρ atau r), yang mengukur derajat korelasi, khususnya hubungan linier antara dua variabel. Koefisien korelasi lainnya, seperti korelasi peringkat Spearman, dirancang agar lebih kuat daripada korelasi Pearson, sehingga lebih sensitif terhadap hubungan non-linier. Konsep saling informasi juga dapat diterapkan untuk mengukur ketergantungan antara dua variabel.

Koefisien momen produk Pearson

Ukuran umum ketergantungan antara dua variabel adalah Koefisien Korelasi Pearson Product Moment (PPMCC), atau yang sering disebut dengan “Koefisien Korelasi Pearson”. Koefisien ini diperoleh dengan mengambil rasio kovarians dua variabel dalam kumpulan data numerik yang dinormalisasi dengan akar kuadrat variansnya. Secara matematis, koefisien ini dihitung dengan membagi kovarians dua variabel dengan produk deviasi standarnya. Karl Pearson mengembangkan koefisien ini berdasarkan gagasan serupa yang dikemukakan oleh Francis Galton.

Koefisien korelasi momen masukan Pearson berupaya menentukan garis yang paling sesuai antara kumpulan data dua variabel dengan menjumlahkan nilai yang diharapkan, dan koefisien ini menunjukkan berapa lama kumpulan data menyimpang dari nilai sebenarnya yang diharapkan. Tanda koefisien korelasi Pearson dapat digunakan untuk menentukan apakah terdapat korelasi negatif atau positif antar variabel data.Koefisien korelasi populasi ρ (rho) antara dua variabel acak X dan Y, nilai yang diharapkan μX dan μY , dan simpangan baku σX dan σY, didefinisikan sebagai :

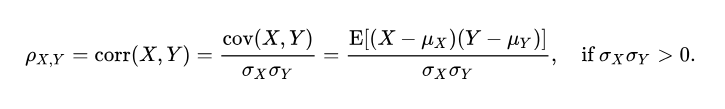
Dimana E adalah operator nilai yang diharapkan, cov menunjukkan kovarians, dan corr adalah notasi alternatif yang banyak digunakan untuk koefisien korelasi. Korelasi Pearson ditentukan hanya jika kedua simpangan baku berhingga dan positif. Rumus alternatif yang hanya berdasarkan momen adalah:

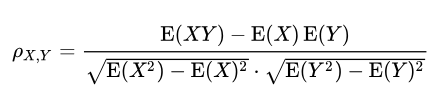
Koefisien korelasi peringkat

Koefisien korelasi peringkat, seperti koefisien korelasi peringkat Spearman dan koefisien korelasi peringkat Kendall (τ), mengukur sejauh mana kenaikan suatu variabel cenderung meningkat pada variabel lain, tanpa peningkatan tersebut harus diwakili oleh hubungan linier. Jika satu variabel meningkat dan variabel lainnya menurun, maka koefisien korelasi ranknya negatif. Koefisien korelasi peringkat umumnya dianggap sebagai alternatif terhadap koefisien Pearson, digunakan untuk mengurangi jumlah perhitungan atau membuat distribusi koefisien kurang sensitif terhadap outlier. Namun, pandangan ini tidak memiliki dasar matematis karena koefisien korelasi peringkat mengukur jenis asosiasi yang berbeda dengan koefisien korelasi product-moment Pearson dan paling baik dipandang sebagai jenis asosiasi yang berbeda daripada ukuran populasi alternatif. koefisien korelasi.

Untuk mengilustrasikan sifat korelasi peringkat dan perbedaannya dengan korelasi linier, perhatikan empat pasang angka berikut

(x, y):(0, 1), (10, 100) , ( 101 , 500) , (102, 2000))

Saat kita berpindah dari setiap pasangan ke pasangan berikutnya, x bertambah dan begitu pula y. Hubungan ini sempurna dalam arti kenaikan x selalu dibarengi dengan kenaikan y. Artinya kita mempunyai korelasi rank yang sempurna dan koefisien korelasi Spearman dan Kendall sebesar 1, sedangkan pada contoh ini koefisien korelasi product-moment Pearson adalah 0,7544, yang menunjukkan bahwa skornya jauh dari garis lurus. Demikian pula, jika y selalu berkurang seiring bertambahnya x, koefisien korelasi peringkatnya adalah -1, sedangkan koefisien korelasi Pearson bisa mendekati -1 tergantung seberapa dekat titik-titik tersebut dengan garis. Meskipun dalam kasus ekstrim korelasi peringkat sempurna kedua koefisien sama (baik +1 atau keduanya -1), hal ini biasanya tidak terjadi, sehingga nilai kedua koefisien tidak dapat dibandingkan secara bermakna. Misalnya, untuk tiga pasangan (1, 1), (2, 3), (3, 2), koefisien Spearman adalah 1/2, sedangkan koefisien Kendall adalah 1/3.

Ukuran ketergantungan lainnya di antara variabel acak

Informasi yang diberikan oleh koefisien korelasi tidak cukup untuk menentukan struktur ketergantungan antar variabel acak. Koefisien korelasi sepenuhnya mendefinisikan struktur ketergantungan hanya dalam kasus yang sangat tertentu, misalnya ketika distribusinya merupakan distribusi normal multivariat. Dalam kasus distribusi elips, hal ini mencirikan elips (hiper) dengan kepadatan yang sama; namun, hal ini tidak sepenuhnya mencirikan struktur ketergantungan (misalnya, derajat kebebasan distribusi t multivariat menentukan tingkat ketergantungan ekor).

Korelasi jarak diperkenalkan untuk mengatasi kekurangan korelasi Pearson yang bisa menjadi nol untuk variabel acak dependen; korelasi jarak nol menyiratkan independensi.

Koefisien Ketergantungan Acak adalah ukuran ketergantungan berbasis kopula yang efisien secara komputasi antara variabel acak multivariat. RDC bersifat invarian terhadap penskalaan variabel acak non-linier, mampu menemukan berbagai pola asosiasi fungsional, dan mengambil nilai nol pada independensi.

Untuk dua variabel biner, rasio odds mengukur ketergantungannya, dan mengambil rentang bilangan non-negatif, kemungkinan tak terhingga: [0, +∞]. Statistik terkait seperti Yule's Y dan Yule's Q menormalkan hal ini ke kisaran seperti korelasi [-1,1]. Rasio kemungkinan digeneralisasikan menggunakan model logistik untuk memodelkan kasus di mana variabel terikatnya bersifat diskrit dan dapat berupa satu atau lebih variabel bebas.

Rasio korelasi, informasi timbal balik berbasis entropi, korelasi total, korelasi berganda total, dan korelasi berganda adalah semuanya. . juga dapat mengidentifikasi ketergantungan yang lebih umum, misalnya dengan mempertimbangkan kopula di antara keduanya, sedangkan koefisien determinasi menggeneralisasi koefisien korelasi menjadi regresi berganda.

Sensitivitas terhadap distribusi data

Derajat ketergantungan antara variabel X dan Y tidak tergantung pada derajat pengungkapan variabel-variabel tersebut. Artinya ketika kita menganalisis hubungan antara X dan Y, perubahan tersebut tidak akan mempengaruhi sebagian besar indikator korelasi. Hal ini berlaku untuk beberapa statistik korelasional dan juga untuk statistik populasi. Beberapa statistik korelasi, seperti koefisien korelasi peringkat, juga invarian terhadap transformasi monotonik dari distribusi marjinal X dan/atau Y.

Koefisien korelasi Pearson/Spearman dalam interval (0,1). Sebagian besar ukuran korelasi sensitif terhadap bagaimana X dan Y diambil sampelnya. Ketergantungan ini biasanya lebih kuat ketika melihat nilai-nilai yang lebih luas. Jadi jika Anda melihat koefisien korelasi antara tinggi badan ayah dan anak laki-laki di antara semua laki-laki dewasa dan membandingkannya dengan koefisien korelasi yang sama yang dihitung ketika ayah dipilih dengan tinggi badan antara 165 dan 170 cm, korelasinya lebih lemah pada anak laki-laki. kasus Beberapa metode telah dikembangkan dan sering digunakan dalam meta-analisis untuk mengoreksi pembatasan rentang pada satu atau kedua variabel; yang paling umum adalah Persamaan Kasus II dan Kasus III Thorndike.

Berbagai ukuran korelasi yang digunakan mungkin tidak terdefinisi untuk distribusi gabungan X dan Y tertentu. Misalnya, koefisien korelasi Pearson didefinisikan dalam momen dan oleh karena itu tidak akan terdefinisi jika momennya tidak terdefinisi. Ukuran ketergantungan berdasarkan kuantil selalu ditentukan. Statistik sampel yang dirancang untuk memperkirakan ukuran ketergantungan populasi mungkin memiliki sifat statistik yang diinginkan, seperti ketidakbiasan atau kontinuitas asimtotik, namun mungkin tidak, berdasarkan struktur spasial populasi dari mana data tersebut berasal.

Sensitivitas terhadap distribusi data. data dapat dieksploitasi. Misalnya, korelasi berskala dirancang untuk menggunakan sensitivitas rentang untuk memilih korelasi antar komponen rangkaian waktu cepat. Dengan memperkecil rentang nilai secara terkendali, korelasi yang terjadi dalam jangka panjang akan tersaring dan hanya korelasi dengan skala waktu pendek yang terungkap.

Disadur dari: en.wikipedia.org

Perancangan Percobaan

Desain eksperimen (DOE atau DOX), juga dikenal sebagai  peracangan percobaan atau desain eksperimen, adalah desain fungsional yang bertujuan untuk mendeskripsikan dan menjelaskan perubahan informasi berdasarkan ukuran yang diusulkan untuk mencerminkan perubahan tersebut. Istilah ini biasanya dikaitkan dengan eksperimen di mana desainnya mencakup ukuran-ukuran yang berkaitan langsung dengan variasi, namun bisa juga merujuk pada desain eksperimen semu di mana faktor-faktor lingkungan dipilih untuk mempengaruhi perbedaan yang seharusnya dilihat tes menetapkan tujuan, Ini memprediksi hasil dengan menggabungkan perubahan masa lalu, yang diwakili oleh satu atau lebih variabel independen, juga disebut “variabel terintegrasi” atau “variabel prediktor.” Dihipotesiskan bahwa perubahan pada satu atau lebih variabel bebas akan menyebabkan perubahan pada satu atau lebih variabel terikat, yang disebut “variabel hasil” atau “variabel respons”.

Desain eksperimental memungkinkan identifikasi variabel kontrol yang harus dijaga konstan agar outlier tidak mempengaruhi hasil. Desain eksperimen tidak hanya terdiri dari pemilihan variabel independen, dependen, dan kontrol yang sesuai, tetapi juga dalam merencanakan pelaksanaan eksperimen dalam kondisi statistik yang paling menguntungkan, dengan mempertimbangkan keterbatasan sumber daya yang tersedia. Ada banyak cara untuk menentukan kumpulan parameter desain (kumpulan unik pengaturan variabel tertentu) untuk digunakan dalam eksperimen.

Perhatian utama dalam desain eksperimen adalah memastikan kekuatan, keandalan, dan kemampuan pengulangan. Misalnya, permasalahan ini dapat diselesaikan sebagian dengan memilih variabel tertentu, mengurangi risiko kesalahan pengukuran, dan menulis prosedur untuk membuat informasi akurat. Masalah terkait mencakup pencapaian tingkat kekuatan dan sensitivitas statistik yang sesuai.

Tes yang dirancang dengan benar diakui sebagai alat utama untuk berhasil menerapkan Quality by Design (QbD) dan metode desain eksperimental yang digunakan di lingkungan, sosial di seluruh dunia, dan Meningkatkan pengetahuan Anda di lapangan teknologi. kerangka Aplikasi lain termasuk pemasaran dan pembuatan kebijakan. Studi tentang desain eksperimental merupakan topik penting dalam metasains.

Sejarah

Teori estimasi statistik, berdasarkan perkembangan statistik reguler, mencakup kontribusi penting dari Charles S. Peirce. Peirce menekankan pentingnya inferensi acak dalam statistik dalam dua publikasinya, "Outline of the Logic of Science" (1877-1878) dan "A Theory of Probable Inference" (1883).

Peirce bergabung dalam inisiatif ini. jalan Metode Uji coba acak dalam pengembangan statistik. Dalam eksperimennya, dia secara acak menugaskan sukarelawan untuk melakukan desain pengukuran buta yang dirancang untuk menilai kemampuan mereka dalam membedakan pemicu stres. Eksperimen Peirce menjadi sumber inspirasi untuk uji coba terkontrol secara acak di bidang psikologi dan pendidikan, yang menghasilkan metode penelitian yang berkembang pada abad ke-19.

Peirce juga berkontribusi pada desain ideal model tereduksi. Pada tahun 1876, ia menerbitkan makalah berbahasa Inggris pertama tentang desain model regresi yang optimal. Gergonne mengusulkan desain optimal untuk regresi polinomial pada tahun 1815, namun Peirce memelopori pengembangan ide ini, dan Kirstine Smith kemudian menerbitkan desain optimal untuk polinomial derajat 6 pada tahun 1918.Menggunakan serangkaian pengujian, di mana Desain masing-masing Pengujian tersebut mungkin bergantung pada hasil pengujian sebelumnya, termasuk kemungkinan keputusan untuk menghentikan pengujian, yang berada dalam area analisis sekuensial.

Abraham Wald memimpin pengembangan konsep ini dalam konteks pengujian hipotesis statistik berurutan. Analisis sekuensial mencakup urutan uji coba, yang dapat mempengaruhi keputusan untuk melanjutkan atau menghentikan uji coba. Herman Chernoff memberikan gambaran umum tentang desain sekuens optimal dan desain adaptif, termasuk desain sekuensial, di S. jax Salah satu jenis desain serial, yang pertama kali dikembangkan oleh Herbert Robbins pada tahun 1952, adalah "penembak jitu dua lengan", yang kemudian diperluas ke teknik penembak jitu multi-lengan.

Prinsip Fisher

Ronald Fisher mengembangkan metode desain eksperimental dalam karya penting "Organization of Field Experiments" (1926) dan "Design of Experiments" (1935). Karyanya, yang berfokus pada penerapan metode statistik pada pertanian, mendorong penggunaan metode ini dalam penelitian biologi, psikologi, dan pertanian.

Dalam penelitian eksperimental, penugasan acak mengacu pada penugasan acak individu ke kelompok berbeda. untuk mendistribusikan Siapkan pidato untuk membandingkan hasil pengobatan. Meskipun risiko ketidakseimbangan antara kelompok perlakuan dan kelompok kontrol harus dikelola, pengacakan mengurangi faktor perancu dan membantu mengidentifikasi efek pengobatan dengan lebih tepat.

Replikasi eksperimental merupakan langkah penting dalam mengatasi inkonsistensi dan ketidakpastian pengukuran; Anda akan dapat mengidentifikasi: Sumber variasi, reliabilitas dan validitas tes. Sebelum replikasi dapat dimulai, persyaratan tertentu harus dipenuhi, seperti menyajikan hasil asli dan upaya replikasi seefisien mungkin.Kendalanya adalah menyusun unit pengujian ke dalam kelompok serupa untuk mengurangi perbedaan antar unit. Ortogonalitas mengacu pada variabel positif dan tidak berkorelasi yang dapat dibandingkan secara langsung. Berbagai desain eksperimen yang membandingkan beberapa faktor secara bersamaan berguna untuk menilai pengaruh dan interaksi faktor. Analisis desain eksperimen mengandalkan analisis varians untuk mengisolasi varians yang diamati.

Disadur dari: en.wikipedia.org

Analisis pohon kesalahan

Analisis pohon kesalahan (FTA) adalah jenis analisis kegagalan yang mengidentifikasi kondisi sistem kritis. Metode analisis ini digunakan dalam rekayasa keselamatan dan rekayasa keandalan untuk memahami bagaimana sistem gagal, mengidentifikasi cara terbaik untuk mengurangi risiko, dan menentukan (atau mendeteksi) kegagalan risiko keselamatan dan tingkat suatu sistem (fungsi). akan digunakan . TLC digunakan dalam industri dirgantara, nuklir, kimia dan pengolahan, farmasi, petrokimia, dan industri berisiko tinggi lainnya. Namun, hal ini juga digunakan di berbagai bidang seperti mengidentifikasi faktor risiko yang terkait dengan kegagalan sistem layanan sosial.

FTA juga digunakan dalam rekayasa perangkat lunak untuk tujuan debugging dan berkaitan erat dengan teknik pemecahan masalah yang digunakan untuk mendeteksi kesalahan. Ini digunakan untuk sesi terakhir. Dari pohon yang salah. Metode-metode ini diklasifikasikan menurut intensitas pengaruhnya. Kasus terburuk memerlukan pemeriksaan log kerusakan. Mekanisme kegagalan dan klasifikasi sistem ini ditentukan dalam analisis risiko operasional.

Penggunaan

Pertama, dapat digunakan untuk memahami logika yang mengarah ke peristiwa teratas atau keadaan yang tidak diinginkan. Analisis ini membuka wawasan tentang bagaimana suatu sistem dapat mengalami kegagalan.

Kedua, analisis pohon kesalahan membantu menunjukkan kepatuhan terhadap persyaratan keamanan dan kehandalan sistem, memastikan bahwa input sistem memenuhi standar keamanan yang ditetapkan.

Selanjutnya, metode ini memungkinkan prioritisasi kontributor yang berujung pada peristiwa teratas, membantu membuat daftar peralatan, suku cadang, atau peristiwa penting untuk berbagai ukuran penting. Hal ini membantu dalam manajemen sumber daya dengan lebih efisien.

Selain itu, analisis pohon kesalahan digunakan untuk memantau dan mengontrol kinerja keselamatan dari sistem kompleks. Misalnya, dapat digunakan untuk menentukan apakah pesawat aman untuk diterbangkan dalam kondisi tertentu atau untuk menghitung batasan waktu ketika suatu komponen tidak berfungsi.

Metode ini juga memiliki peran penting dalam meminimalkan dan mengoptimalkan sumber daya, mengidentifikasi cara terbaik untuk mengelola aset dan menjaga kinerja sistem secara optimal.

Selain itu, analisis pohon kesalahan berfungsi sebagai alat diagnostik untuk mengidentifikasi dan memperbaiki penyebab kejadian puncak. Ini memberikan panduan yang berguna untuk pengembangan manual atau proses diagnostik, membantu dalam upaya perbaikan dan pemeliharaan sistem secara keseluruhan.

Terakhir, FTA dapat menjadi alat desain yang membantu merancang suatu sistem, membantu menciptakan persyaratan yang lebih rendah atau output yang diinginkan. Oleh karena itu, analisis pohon kesalahan memainkan peran penting dalam siklus hidup sistem mulai dari desain hingga pemeliharaan.

Sejarah

Fault Tree Analysis (FTA) awalnya dikembangkan oleh H.A. H.A., disewa oleh AS Divisi Sistem Balistik Angkatan Udara akan mengevaluasi sistem kendali peluncuran rudal balistik antarbenua (ICBM) Minuteman I. Sistem ini didukung secara luas, sering didukung, dan telah digunakan sebagai alat analisis yang andal oleh para ahli tepercaya. Setelah pengumuman pertama penggunaan FTA dalam penelitian keselamatan operasional Minuteman pada tahun 1962, Boeing dan AVCO memperluas penggunaan FTA ke seluruh sistem Minuteman II pada tahun 1963–1964. FTA dibahas pada Simposium Keamanan Sistem tahun 1965 di Seattle, yang disponsori oleh Boeing dan Universitas Washington. Boeing mulai menggunakan FTA dalam desain pesawat sipil sekitar tahun 1966.Kemudian di Angkatan Darat AS, Picatinny Arsenal mengeksplorasi penerapan FTA untuk digunakan dengan cakupan pada tahun 1960an dan 1970an. Pada tahun 1976, Amerika Komando Materiel Angkatan Darat telah memasukkan FTA ke dalam Manual Desain Teknis untuk Desain untuk Keandalan. Institut Pertahanan Roma dan penerusnya, sekarang Pusat Informasi Teknis Pertahanan (sekarang Pusat Analisis Informasi Sistem Pertahanan), telah menerbitkan artikel tentang TLC dan desain blok keandalan sejak tahun 1960an. MIL -HDBK-338B adalah referensi yang lebih baru.

Pada tahun 1970, Administrasi Penerbangan Federal (FAA) menerbitkan Peraturan Kelaikan Udara untuk Pesawat Kategori Transportasi dalam Daftar Federal pada 35 FR 5665 (1970 -04), 14 CFR . ubah untuk 25.1309. - 08). Perubahan ini menyebabkan berkurangnya standar ketat untuk sistem dan peralatan pesawat terbang serta meluasnya penggunaan FTA dalam penerbangan. Pada tahun 1998, FAA mengeluarkan Perintah 8040.4, yang menetapkan kebijakan manajemen risiko, termasuk analisis risiko, untuk beberapa aktivitas penting selain sertifikasi pesawat, termasuk pengoperasian pesawat dan pembaruan AS. Sistem Wilayah Udara Nasional. Hal ini menyebabkan diterbitkannya Manual Keamanan Sistem FAA, yang menjelaskan penggunaan FTA dalam berbagai analisis risiko formal.Pada awal program Apollo, muncul pertanyaan tentang kemampuan mengirim astronot ke Bulan dan kembali lagi. Tinggal di pedesaan Perhitungan risiko atau keandalan dilakukan dan hasilnya menunjukkan bahwa kemungkinan keberhasilan misi sangat rendah.

Hasil ini menghalangi NASA untuk melakukan pengukuran risiko atau uji diagnostik lebih lanjut hingga setelah bencana Challenger pada tahun 1986. Sebaliknya, NASA memutuskan untuk menggunakan Mode Kegagalan dan Penilaian Dampak (FMEA) dan metode kualifikasi lainnya untuk menilai keamanan sistem. Setelah bencana Challenger, pentingnya penilaian risiko probabilistik (PRA) dan FTA dalam analisis risiko dan keandalan sistem diakui, dan penggunaannya di NASA mulai meningkat, dan FTA sekarang dianggap sebagai salah satu metode analisis keselamatan dan keandalan sistem yang paling penting.

Dalam industri tenaga nuklir, Komisi Pengaturan Nuklir AS mulai menggunakan prosedur PRA, termasuk FTA, pada tahun 1975, dan memperluas penelitian PRA setelah kecelakaan Three Mile Island tahun 1979. Hal ini akhirnya mengarah pada penerbitan NRC Defect Tree Manual NUREG-0492 pada tahun 1981 dan resep PRA oleh Administrator NRC. Administrasi Keselamatan dan Kesehatan Kerja (OSHA) dari Departemen Tenaga Kerja AS menerbitkan standar manajemen keselamatan (PSM) pada 19 CFR 1910.119 dalam Daftar Federal di 57 FR 6356 (24/02/1992). OSHA PSM mengakui FTA sebagai metode yang diterima untuk analisis bahaya proses (PHA).Saat ini, FTA banyak digunakan dalam rekayasa keselamatan dan keandalan sistem serta dalam semua teknik rekayasa utama.

Metodologi

Standar FTA mencakup NRC NUREG-0492 untuk industri nuklir, Aerospace Focused Evaluation NUREG-0492 untuk penggunaan NASA, SAE ARP4761 untuk industri dirgantara sipil, MIL-HDBK-338 untuk sistem militer, dan IEC 61025 untuk operasi transfer. dirancang untuk digunakan dan telah diadopsi sebagai standar Eropa EN 61025.

Bahkan sistem yang paling rumit pun dapat gagal karena kegagalan satu atau lebih subsistem. Namun risiko kegagalan dapat dikurangi dengan memperbaiki desain sistem. Analisis pohon kesalahan membuat diagram logika lengkap, memetakan hubungan antara kesalahan, subsistem, dan elemen desain keselamatan utama.

Hasil yang tidak diinginkan disebut akar (“kejadian utama”) dari pohon logika. Misalnya, dampak negatif dari proses penajaman tekanan logam diduga adalah keterikatan manusia. Melihat kembali peristiwa-peristiwa besar ini, kita dapat melihat bahwa hal ini dapat terjadi dalam dua cara: selama aktivitas normal atau selama aktivitas pemeliharaan. Kondisi ini logis OR. Jika kita memikirkan kecelakaan yang terjadi selama pengoperasian normal, kita dapat menyimpulkan bahwa hal ini dapat terjadi melalui dua cara. Artinya, menekan kawat dapat menimbulkan kerugian bagi pekerja, sedangkan menekan kawat dapat menimbulkan kerugian bagi orang lain. Ini adalah OR logis lainnya. Desainnya dapat diperbaiki dengan mengharuskan operator menekan dua tombol terpisah untuk memutar alat berat. Ini adalah operasi yang aman dalam mode AND yang logis. Tingkat kesalahan konversi. Ini menjadi alarm kesalahan yang dapat didekodekan.

Pohon kesalahan menunjukkan bilangan real untuk probabilitas kesalahan, dan program perangkat lunak dapat menghitung probabilitas kesalahan dari pohon kesalahan. Bila diketahui suatu peristiwa mempunyai lebih dari satu akibat, yaitu mempengaruhi beberapa subsistem, maka disebut penyebab umum atau mekanisme umum. Peristiwa ini biasanya terjadi di banyak area pohon. Penyebab umum menciptakan hubungan ketergantungan antar peristiwa. Penghitungan jauh lebih rumit untuk pohon yang memiliki banyak penyebab umum dibandingkan pohon yang semua kejadiannya dianggap independen. Tidak semua perangkat lunak yang tersedia secara komersial melakukan hal ini.

Pohon dibuat menggunakan simbol gerbang logika yang ada. Cut set adalah sekumpulan kejadian (biasanya kegagalan komponen) yang menghasilkan kejadian tinggi. Jika suatu peristiwa tidak dapat dihilangkan dari rangkaian pemotongan tanpa menghasilkan peristiwa yang tinggi, maka peristiwa tersebut disebut rangkaian pemotongan rendah.

Beberapa industri menggunakan pohon kesalahan dan pohon peristiwa (lihat Penilaian Potensi Risiko). Pohon kejadian dimulai dengan pemicu yang tidak diinginkan (kehilangan item penting, kegagalan komponen, dll.) dan mengikuti kejadian sistem lainnya hingga rangkaian produk akhir. Ketika setiap peristiwa baru dipertimbangkan, sebuah simpul baru ditambahkan ke pohon dengan membaginya dengan probabilitas bahwa salah satu cabang dihilangkan. Anda dapat melihat kemungkinan bahwa sejumlah "proyek akhir" akan muncul dari sesi awal yang digunakan di banyak pembangkit listrik tenaga nuklir AS dan sebagian besar wilayah AS. SAPHIRE dari Laboratorium Nasional Idaho digunakan oleh produsen, pelanggan internasional, dan pemerintah AS untuk menilai keamanan dan keandalan reaktor nuklir, pesawat ruang angkasa, dan Stasiun Luar Angkasa Internasional. Di luar Amerika Serikat, perangkat lunak RiskSpectrum adalah alat yang banyak digunakan untuk analisis pohon kesalahan dan kegagalan serta dilisensikan untuk digunakan di lebih dari 60% pembangkit listrik tenaga nuklir di seluruh dunia untuk penilaian potensi keselamatan. Perangkat lunak gratis tingkat profesional tersedia secara luas. SCRAM adalah alat sumber terbuka yang mengimplementasikan format pertukaran model Open-PSA standar terbuka untuk aplikasi penilaian keamanan potensial.

Simbol Grafis

Sinyal dasar yang digunakan dalam FTA dibagi menjadi sinyal perakitan, gateway dan sinyal transisi. Perbedaan kecil dapat digunakan dalam perangkat lunak FTA.

Simbol Acara

Tag peristiwa digunakan untuk peristiwa besar dan menengah. Peristiwa besar tidak terjadi dalam sistem yang salah. Peristiwa perantara dapat ditemukan di jalan keluar. Gejala-gejala kejadian tersebut adalah sebagai berikut :

Kode peristiwa default digunakan sebagai berikut: Peristiwa Utama: Kegagalan atau kesalahan komponen atau elemen sistem, misalnya sakelar macet di posisi terbuka. Peristiwa Eksternal: Sesuatu yang seharusnya terjadi (tidak salah). Insiden yang belum dijelajahi: Insiden yang informasinya tidak mencukupi atau insiden tanpa hasil. Konfigurasikan Peristiwa: Metode yang membatasi atau memengaruhi gerbang logika (misalnya mode kontrol tipikal) Untuk memberikan lebih banyak ruang untuk memasukkan deskripsi peristiwa, gerbang peristiwa perantara dapat digunakan lebih dari sekadar peristiwa utama. FTA adalah pendekatan top-down.

Simbol Gerbang

Simbol gerbang mewakili hubungan antara kejadian masukan dan keluaran. Simbol-simbol ini berasal dari simbol logika boolean.

Fungsi gerbangnya adalah: Gerbang OR: Terjadi masukan dan keluar. Gerbang AND: Output terjadi jika semua input terjadi (input tidak bergantung pada sumbernya). Gerbang OR Eksklusif: Output terjadi ketika hanya satu input yang muncul. DAN Gerbang Utama - Urutan Keluaran terjadi ketika masukan terjadi dalam urutan tertentu yang ditentukan oleh kondisi situasi. Gerbang penghambat: Keluaran terjadi ketika masukan berada dalam kondisi aktivasi yang ditentukan oleh peristiwa tertentu.

Simbol Transfer

Sinyal transport digunakan untuk menghubungkan input dan output dari pohon kesalahan terkait, seperti subsistem, ke sistem tersebut. NASA telah menyiapkan artikel lengkap tentang FTA dan proyek nyata.

Disadur dari: en.wikipedia.org