Korelasi
Dalam statistik, korelasi atau ketergantungan mengacu pada hubungan statistik antara dua variabel acak atau data bivariat, baik kausal atau tidak. Khususnya dalam konteks statistik, istilah "korelasi" sering kali mengacu pada derajat hubungan linier antara sepasang variabel. Contoh fenomena dependen adalah hubungan antara tinggi badan orang tua dan keturunannya, serta hubungan antara harga suatu barang dan jumlah yang dibeli oleh konsumen, seperti yang ditunjukkan pada kurva permintaan.
Korelasi berguna karena dapat menunjukkan prediksi. hubungan yang dapat digunakan dalam praktek. Misalnya, sebuah perusahaan utilitas mungkin menghasilkan lebih sedikit listrik pada siang hari berdasarkan korelasi antara permintaan listrik dan cuaca. Dalam situasi ini terdapat hubungan sebab akibat dimana kondisi cuaca ekstrim memaksa masyarakat untuk menggunakan lebih banyak listrik untuk pemanas atau pendingin. Pada saat yang sama, perlu dicatat bahwa keberadaan korelasi tidak cukup untuk menyimpulkan adanya hubungan sebab akibat, karena korelasi tidak selalu menunjukkan hubungan sebab akibat.
Secara formal, korelasi dianggap sebagai variabel acak. bergantung jika tidak memenuhi sifat matematis dari kemungkinan independensi. Dalam istilah teknis, korelasi dapat merujuk pada berbagai operasi matematika spesifik antara variabel yang diuji dan nilai yang diharapkan terkait. Beberapa koefisien korelasi yang umum digunakan, seperti koefisien korelasi Pearson (sering dilambangkan dengan ρ atau r), yang mengukur derajat korelasi, khususnya hubungan linier antara dua variabel. Koefisien korelasi lainnya, seperti korelasi peringkat Spearman, dirancang agar lebih kuat daripada korelasi Pearson, sehingga lebih sensitif terhadap hubungan non-linier. Konsep saling informasi juga dapat diterapkan untuk mengukur ketergantungan antara dua variabel.
Koefisien momen produk Pearson
Ukuran umum ketergantungan antara dua variabel adalah Koefisien Korelasi Pearson Product Moment (PPMCC), atau yang sering disebut dengan “Koefisien Korelasi Pearson”. Koefisien ini diperoleh dengan mengambil rasio kovarians dua variabel dalam kumpulan data numerik yang dinormalisasi dengan akar kuadrat variansnya. Secara matematis, koefisien ini dihitung dengan membagi kovarians dua variabel dengan produk deviasi standarnya. Karl Pearson mengembangkan koefisien ini berdasarkan gagasan serupa yang dikemukakan oleh Francis Galton.
Koefisien korelasi momen masukan Pearson berupaya menentukan garis yang paling sesuai antara kumpulan data dua variabel dengan menjumlahkan nilai yang diharapkan, dan koefisien ini menunjukkan berapa lama kumpulan data menyimpang dari nilai sebenarnya yang diharapkan. Tanda koefisien korelasi Pearson dapat digunakan untuk menentukan apakah terdapat korelasi negatif atau positif antar variabel data.Koefisien korelasi populasi ρ (rho) antara dua variabel acak X dan Y, nilai yang diharapkan μX dan μY , dan simpangan baku σX dan σY, didefinisikan sebagai :
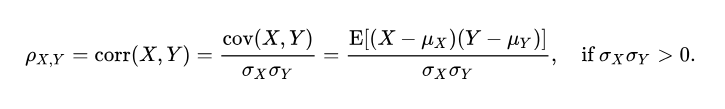
Dimana E adalah operator nilai yang diharapkan, cov menunjukkan kovarians, dan corr adalah notasi alternatif yang banyak digunakan untuk koefisien korelasi. Korelasi Pearson ditentukan hanya jika kedua simpangan baku berhingga dan positif. Rumus alternatif yang hanya berdasarkan momen adalah:
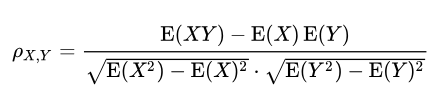
Koefisien korelasi peringkat
Koefisien korelasi peringkat, seperti koefisien korelasi peringkat Spearman dan koefisien korelasi peringkat Kendall (τ), mengukur sejauh mana kenaikan suatu variabel cenderung meningkat pada variabel lain, tanpa peningkatan tersebut harus diwakili oleh hubungan linier. Jika satu variabel meningkat dan variabel lainnya menurun, maka koefisien korelasi ranknya negatif. Koefisien korelasi peringkat umumnya dianggap sebagai alternatif terhadap koefisien Pearson, digunakan untuk mengurangi jumlah perhitungan atau membuat distribusi koefisien kurang sensitif terhadap outlier. Namun, pandangan ini tidak memiliki dasar matematis karena koefisien korelasi peringkat mengukur jenis asosiasi yang berbeda dengan koefisien korelasi product-moment Pearson dan paling baik dipandang sebagai jenis asosiasi yang berbeda daripada ukuran populasi alternatif. koefisien korelasi.
Untuk mengilustrasikan sifat korelasi peringkat dan perbedaannya dengan korelasi linier, perhatikan empat pasang angka berikut
(x, y):(0, 1), (10, 100) , ( 101 , 500) , (102, 2000))
Saat kita berpindah dari setiap pasangan ke pasangan berikutnya, x bertambah dan begitu pula y. Hubungan ini sempurna dalam arti kenaikan x selalu dibarengi dengan kenaikan y. Artinya kita mempunyai korelasi rank yang sempurna dan koefisien korelasi Spearman dan Kendall sebesar 1, sedangkan pada contoh ini koefisien korelasi product-moment Pearson adalah 0,7544, yang menunjukkan bahwa skornya jauh dari garis lurus. Demikian pula, jika y selalu berkurang seiring bertambahnya x, koefisien korelasi peringkatnya adalah -1, sedangkan koefisien korelasi Pearson bisa mendekati -1 tergantung seberapa dekat titik-titik tersebut dengan garis. Meskipun dalam kasus ekstrim korelasi peringkat sempurna kedua koefisien sama (baik +1 atau keduanya -1), hal ini biasanya tidak terjadi, sehingga nilai kedua koefisien tidak dapat dibandingkan secara bermakna. Misalnya, untuk tiga pasangan (1, 1), (2, 3), (3, 2), koefisien Spearman adalah 1/2, sedangkan koefisien Kendall adalah 1/3.
Ukuran ketergantungan lainnya di antara variabel acak
Informasi yang diberikan oleh koefisien korelasi tidak cukup untuk menentukan struktur ketergantungan antar variabel acak. Koefisien korelasi sepenuhnya mendefinisikan struktur ketergantungan hanya dalam kasus yang sangat tertentu, misalnya ketika distribusinya merupakan distribusi normal multivariat. Dalam kasus distribusi elips, hal ini mencirikan elips (hiper) dengan kepadatan yang sama; namun, hal ini tidak sepenuhnya mencirikan struktur ketergantungan (misalnya, derajat kebebasan distribusi t multivariat menentukan tingkat ketergantungan ekor).
Korelasi jarak diperkenalkan untuk mengatasi kekurangan korelasi Pearson yang bisa menjadi nol untuk variabel acak dependen; korelasi jarak nol menyiratkan independensi.
Koefisien Ketergantungan Acak adalah ukuran ketergantungan berbasis kopula yang efisien secara komputasi antara variabel acak multivariat. RDC bersifat invarian terhadap penskalaan variabel acak non-linier, mampu menemukan berbagai pola asosiasi fungsional, dan mengambil nilai nol pada independensi.
Untuk dua variabel biner, rasio odds mengukur ketergantungannya, dan mengambil rentang bilangan non-negatif, kemungkinan tak terhingga: [0, +∞]. Statistik terkait seperti Yule's Y dan Yule's Q menormalkan hal ini ke kisaran seperti korelasi [-1,1]. Rasio kemungkinan digeneralisasikan menggunakan model logistik untuk memodelkan kasus di mana variabel terikatnya bersifat diskrit dan dapat berupa satu atau lebih variabel bebas.
Rasio korelasi, informasi timbal balik berbasis entropi, korelasi total, korelasi berganda total, dan korelasi berganda adalah semuanya. . juga dapat mengidentifikasi ketergantungan yang lebih umum, misalnya dengan mempertimbangkan kopula di antara keduanya, sedangkan koefisien determinasi menggeneralisasi koefisien korelasi menjadi regresi berganda.
Sensitivitas terhadap distribusi data
Derajat ketergantungan antara variabel X dan Y tidak tergantung pada derajat pengungkapan variabel-variabel tersebut. Artinya ketika kita menganalisis hubungan antara X dan Y, perubahan tersebut tidak akan mempengaruhi sebagian besar indikator korelasi. Hal ini berlaku untuk beberapa statistik korelasional dan juga untuk statistik populasi. Beberapa statistik korelasi, seperti koefisien korelasi peringkat, juga invarian terhadap transformasi monotonik dari distribusi marjinal X dan/atau Y.
Koefisien korelasi Pearson/Spearman dalam interval (0,1). Sebagian besar ukuran korelasi sensitif terhadap bagaimana X dan Y diambil sampelnya. Ketergantungan ini biasanya lebih kuat ketika melihat nilai-nilai yang lebih luas. Jadi jika Anda melihat koefisien korelasi antara tinggi badan ayah dan anak laki-laki di antara semua laki-laki dewasa dan membandingkannya dengan koefisien korelasi yang sama yang dihitung ketika ayah dipilih dengan tinggi badan antara 165 dan 170 cm, korelasinya lebih lemah pada anak laki-laki. kasus Beberapa metode telah dikembangkan dan sering digunakan dalam meta-analisis untuk mengoreksi pembatasan rentang pada satu atau kedua variabel; yang paling umum adalah Persamaan Kasus II dan Kasus III Thorndike.
Berbagai ukuran korelasi yang digunakan mungkin tidak terdefinisi untuk distribusi gabungan X dan Y tertentu. Misalnya, koefisien korelasi Pearson didefinisikan dalam momen dan oleh karena itu tidak akan terdefinisi jika momennya tidak terdefinisi. Ukuran ketergantungan berdasarkan kuantil selalu ditentukan. Statistik sampel yang dirancang untuk memperkirakan ukuran ketergantungan populasi mungkin memiliki sifat statistik yang diinginkan, seperti ketidakbiasan atau kontinuitas asimtotik, namun mungkin tidak, berdasarkan struktur spasial populasi dari mana data tersebut berasal.
Sensitivitas terhadap distribusi data. data dapat dieksploitasi. Misalnya, korelasi berskala dirancang untuk menggunakan sensitivitas rentang untuk memilih korelasi antar komponen rangkaian waktu cepat. Dengan memperkecil rentang nilai secara terkendali, korelasi yang terjadi dalam jangka panjang akan tersaring dan hanya korelasi dengan skala waktu pendek yang terungkap.
Disadur dari: en.wikipedia.org