Uji Chi-Kuadrat
Uji chi-kuadrat (juga uji chi-kuadrat atau χ2) adalah uji hipotesis statistik yang digunakan dalam analisis tabel kontingensi ketika ukuran sampel besar. Secara sederhana, uji ini terutama digunakan untuk memeriksa apakah dua variabel kategorikal (dua dimensi dari tabel kontingensi) bersifat independen dalam mempengaruhi statistik uji (nilai dalam tabel).Uji ini valid jika statistik uji terdistribusi secara chi-kuadrat di bawah hipotesis nol, khususnya uji chi-kuadrat Pearson dan varian-variannya. Uji chi-kuadrat Pearson digunakan untuk menentukan apakah ada perbedaan yang signifikan secara statistik antara frekuensi yang diharapkan dan frekuensi yang diamati dalam satu atau lebih kategori tabel kontingensi. Untuk tabel kontingensi dengan ukuran sampel yang lebih kecil, uji eksak Fisher digunakan sebagai gantinya.
Dalam aplikasi standar uji ini, pengamatan diklasifikasikan ke dalam kelas-kelas yang saling terpisah. Jika hipotesis nol yang menyatakan bahwa tidak ada perbedaan antara kelas-kelas dalam populasi adalah benar, maka statistik uji yang dihitung dari pengamatan mengikuti distribusi frekuensi χ2. Tujuan dari pengujian ini adalah untuk mengevaluasi seberapa besar kemungkinan frekuensi yang diamati dengan asumsi hipotesis nol benar.
Statistik uji yang mengikuti distribusi χ2 terjadi ketika observasi bersifat independen. Ada juga uji χ2 untuk menguji hipotesis nol independensi dari sepasang variabel acak berdasarkan pengamatan terhadap pasangan tersebut.
Uji chi-kuadrat sering kali merujuk pada uji yang distribusi statistik uji mendekati distribusi χ2 secara asimtotik, yang berarti bahwa distribusi sampling (jika hipotesis nol benar) dari statistik uji mendekati distribusi chi-kuadrat semakin mendekati distribusi chi-kuadrat seiring dengan bertambahnya jumlah sampel.
Sejarah
Pada abad ke-19, metode analisis statistik terutama diterapkan dalam analisis data biologis dan merupakan kebiasaan bagi para peneliti untuk mengasumsikan bahwa pengamatan mengikuti distribusi normal, seperti Sir George Airy dan Mansfield Merriman, yang karyanya dikritik oleh Karl Pearson dalam makalahnya pada tahun 1900.
Pada akhir abad ke-19, Pearson menyadari adanya kemencengan yang signifikan dalam beberapa pengamatan biologis. Untuk memodelkan pengamatan terlepas dari normal atau miring, Pearson, dalam serangkaian artikel yang diterbitkan dari tahun 1893 hingga 1916, merancang distribusi Pearson, keluarga distribusi probabilitas kontinu, yang mencakup distribusi normal dan banyak distribusi miring, dan mengusulkan metode analisis statistik yang terdiri dari penggunaan distribusi Pearson untuk memodelkan pengamatan dan melakukan uji kecocokan (test of goodness of fit) untuk menentukan seberapa baik model tersebut benar-benar sesuai dengan pengamatan.
Uji Chi-Kuadrat Pearson
Pada tahun 1900, Pearson menerbitkan sebuah makalah tentang uji χ2 yang dianggap sebagai salah satu fondasi statistik modern. Dalam makalah ini, Pearson menginvestigasi uji kecocokan (goodness of fit).
Misalkan n pengamatan dalam sampel acak dari sebuah populasi diklasifikasikan ke dalam k kelas yang saling terpisah dengan masing-masing jumlah pengamatan xi (untuk i = 1,2,...,k), dan hipotesis nol memberikan probabilitas pi bahwa sebuah pengamatan masuk ke dalam kelas ke-i. Jadi kita memiliki angka yang diharapkan mi = npi untuk semua i, di mana :
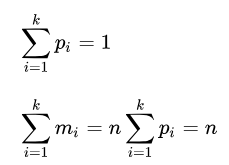
Pearson berasumsi bahwa, dalam situasi di mana hipotesis nol benar, n → tidak terbatas, maka distribusi batas bawah adalah distribusi χ2.
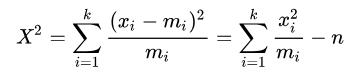
Pearson pertama kali menyatakan kasus bahwa angka yang diharapkan adalah angka besar yang diketahui semua sel, dengan asumsi bahwa setiap pengamatan. χ 2 dan k − 1 derajat kebebasan.Namun, Pearson mempertimbangkan kasus di mana nilai yang diharapkan bergantung pada parameter yang ditentukan dalam model dan berasumsi bahwa indikator m i bilangan real dan m: ' I adalah bilangan yang diharapkan, yang mana berbeda.

Pearson pertama kali membahas kasus bahwa angka yang diharapkan (mi) adalah angka kritis yang diketahui semua sel, dengan asumsi bahwa setiap pengamatan (xi) dapat didistribusikan secara acak, dan ketika n, kita sampai pada hasil X^2 di wilayah tersebut. Ini mengikuti distribusi chi-kuadrat dengan derajat kebebasan (k - 1).Namun, Pearson mempertimbangkan kasus di mana angka yang diharapkan di masa depan bergantung pada parameter yang ditentukan dalam contoh dan alasan, menggunakan notasi mi: angka dan m ' Saya adalah perkiraannya, perbedaannya.
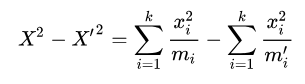
Biasanya, kesalahan perkiraan ini akan positif dan cukup kecil untuk dihilangkan. Sebagai kesimpulan, Pearson berpendapat bahwa jika kita menganggap (X'^2) juga terdistribusi sebagai distribusi chi-kuadrat dengan (k - 1) derajat kebebasan, kesalahan dalam perkiraan ini tidak akan mempengaruhi keputusan praktis. Kesimpulan ini menimbulkan beberapa kontroversi dalam penerapan praktisnya dan baru diselesaikan selama 20 tahun hingga makalah Fisher tahun 1922 dan 1924.
Contoh lain dari uji Chi-kuadrat
Contoh lain dari uji chi-kuadrat adalah penggunaannya untuk memeriksa apakah varians suatu populasi yang berdistribusi normal mempunyai nilai tertentu berdasarkan varians sampel. Meskipun pengujian ini jarang dilakukan dalam praktiknya karena varians populasi tidak diketahui, ada beberapa statistik yang dapat digunakan untuk memperkirakan distribusi chi-kuadrat resmi.
Contohnya adalah uji eksak Fisher. Untuk menguji kemandirian, kami melakukan uji chi - 2 × 2. Terdapat juga uji binomial yang dapat digunakan sebagai alternatif uji chi-kuadrat 2 × 1 untuk menentukan goodness of fit.Beberapa uji chi lainnya persegi uji chi-kuadrat Cochran-Mantel-Haenszel digunakan. Uji kuadrat, uji McNemar digunakan untuk beberapa tabel berpasangan 2×2, uji korelasi Tukey dan uji Portmanteau dalam analisis deret waktu untuk menguji autokorelasi. Selain itu, uji rasio kemungkinan dalam pemodelan statistik digunakan untuk menguji apakah akan berpindah dari model sederhana ke model yang lebih kompleks yang berisi model sederhana.
Disadur dari: en.wikipedia.org