Algoritma semut

Diperkenalkan oleh Moyson dan Manderick dan dikembangkan secara ekstensif oleh Marco Dorigo, algoritma Ant adalah teknik probabilistik untuk memecahkan masalah komputasi dengan menemukan jalur terbaik melalui grafik. Algoritme ini terinspirasi oleh perilaku semut saat mereka mencari jalan dari koloni menuju makanan.

Di dunia nyata, semut berkeliaran secara acak dan ketika menemukan makanan, mereka kembali ke koloninya, mengirimkan sinyal melalui jejak feromon. Ketika semut lain menemukan jejaknya, mereka tidak lagi berkeliaran secara acak tetapi mengikuti jejak tersebut dan kembali serta memperkuatnya ketika mereka akhirnya menemukan makanan.

Namun, seiring berjalannya waktu, jejak feromon akan hilang dan kekuatan tarik-menariknya akan berkurang. Semakin lama semut bergerak bolak-balik sepanjang jalur ini, semakin lama pula feromonnya menguap. Sebagai perbandingan, jalur pendek akan lebih cepat sejajar dan oleh karena itu kepadatan feromon tetap tinggi karena ia bergerak secepat penguapannya.Penguapan feromon juga mempunyai keuntungan dalam menghindari konvergensi menuju solusi optimal lokal. Jika tidak terjadi penguapan, jalur yang dipilih semut pertama akan cenderung terlalu menarik bagi semut berikutnya. Dalam kasus seperti ini, eksplorasi ruang solusi menjadi terbatas.

Jadi jika seekor semut menemukan jalur yang baik (jalur pendek) dari koloni menuju sumber makanan, semut lain akan mengikuti jalur tersebut, dan pada akhirnya semua semut akan mengikuti satu jalur. Ide dari algoritma koloni semut adalah untuk meniru perilaku ini melalui “semut buatan” yang berjalan mengelilingi grafik yang mewakili masalah yang harus dipecahkan

.Algoritma optimisasi koloni semut telah digunakan untuk menghasilkan penyelesaian yang mendekati optimal pada masalah salesman yang melakukan perjalanan. Algoritme semut lebih menguntungkan daripada pendekatan penguatan tiruan (simulaten annealing) dan algoritme genetik saat grafik mungkin berubah secara dinamis; algoritme koloni semut dapat berjalan secara kontinu dan menyesuaikan dengan perubahan secara waktu nyata (real time). Hal ini menarik dalam routing jaringan dan sistem transportasiurban.

Algoritma dan Rumus 

Dalam algoritma optimasi koloni semut, semut buatan bertindak sebagai agen komputasi sederhana yang tujuannya adalah menemukan solusi optimal untuk masalah optimasi yang diberikan. Untuk menerapkan algoritma ini, masalah optimasi harus diubah menjadi masalah pencarian jalur terpendek dalam graf berbobot. Pada langkah pertama setiap iterasi, setiap semut secara stokastik membangun solusi dengan menyusun rangkaian sisi dalam grafik. Langkah kedua adalah membandingkan jalur yang ditemukan oleh semut yang berbeda. Langkah terakhir adalah memperbarui nilai feromon pada setiap sisi grafik.Dengan pendekatan ini, setiap semut berkontribusi dalam pencarian solusi optimal, menciptakan kolaborasi dan kemampuan beradaptasi untuk menemukan jalur terpendek menuju masalah optimasi tertentu.

Aplikasi

Algoritme optimasi koloni semut telah diterapkan pada banyak masalah optimasi kombinatorial mulai dari penugasan kuadrat hingga pelipatan protein atau perutean kendaraan, dan banyak metode turunan telah disesuaikan dengan masalah dinamis dalam variabel nyata, masalah stokastik, tujuan ganda, dan implementasi paralel. Ini juga telah digunakan untuk menemukan solusi yang mendekati optimal terhadap masalah penjual. Mereka memiliki keunggulan dibandingkan pendekatan simulasi anildan algoritma genetika untuk masalah serupa ketika grafik dapat berubah secara dinamis; Algoritma koloni semut dapat berjalan terus menerus dan beradaptasi terhadap perubahan secara real time. Hal ini menarik untuk perutean jaringan dan sistem transportasi perkotaan.

Algoritma ACO, seperti Ant System, mengimplementasikan seperangkat aturan yang terinspirasi oleh perilaku semut biologis. Setiap semut dalam algoritma ini memiliki tujuan untuk mengunjungi setiap kota tepat satu kali dalam perjalanan yang dipilih. Konsep visibilitas diterapkan, dengan kota-kota yang lebih jauh mempunyai kemungkinan yang lebih kecil untuk dipilih, hal ini mencerminkan kecenderungan semut untuk memilih jalur yang lebih dekat. Selain itu, keberhasilan suatu tepi dalam melakukan perjalanan dipengaruhi oleh kekuatan jejak feromon yang ada pada tepi tersebut. Semakin kuat jejak feromon, semakin besar kemungkinan semut memilih tepian tersebut.

Setelah menyelesaikan perjalanannya, semut menyimpan feromon tambahan di semua sisi jalurnya, terutama jika perjalanannya singkat.Hal ini mencerminkan cara semut biologis meninggalkan jejak feromon untuk memandu temannya menuju sumber daya yang mereka temukan. Namun, untuk menghindari konvergensi menuju solusi optimal lokal, jejak feromon menghilang setelah setiap iterasi. Pendekatan ini menciptakan dinamika yang mirip dengan siklus alami semut biologis, di mana feromon yang ditinggalkan semut sebelumnya secara bertahap berkurang seiring berjalannya waktu. Dengan menerapkan aturan-aturan ini, algoritma ACO menghasilkan totalsolusi optimal atau mendekati optimal terhadap masalah penjual yang kompleks. 

Masalah Penjadwalan

Permasalahan perencanaan produksi meliputi Sequential Order Problem (SOP), Job Shop Scheduling Problem (JSP), Open Shop Scheduling Problem (OSP), Permutation Flow Shop Problem (PFSP), Single Machine Total Lateness Problem (SMTTP) dan masalah penundaan. Single Machine Weighted Total (SMTWTP), Resource Constrained Project Scheduling Problem (RCPSP), Group Shop Scheduling Problem (GSP), Single Machine Total Delay Problem dengan Time Sequence Dependent Configuration(SMTTPDST), Multistage Flow Shop Scheduling Problem (MFSP) dengan Sequence Waktu Pengaturan/perubahan yang bergantung dan masalah Perencanaan Urutan Perakitan (ASP).

Masalah perutean kendaraan 

Permasalahan pada domain routing kendaraan mencakup berbagai aspek seperti capacity vehicle routing problem (CVRP), multi-depot vehicle routing problem (MDVRP), periodic vehicle routing problem (PVRP), split delivery vehicle routing problem (SDVRP) dan permasalahan berkendara. kendaraan. Masalah Stokastik (SVRP), Masalah Perutean Kendaraan dengan Penjemputan dan Pengantaran (VRPPD), Masalah Perutean Kendaraan dengan Jendela Waktu (VRPTW), Masalah Perutean KendaraanBergantung Waktu dengan Waktu Jendela Waktu (TDVRPTW) dan Masalah Perutean Kendaraan dengan Waktu dan Waktu Pekerja Layanan Multi-Jendela (VRPTWMS).

Sumber: id.wikipedia.org

Algoritme genetik

Algoritma genetika adalah teknik pencarian dalam ilmu komputer untuk menemukan solusi perkiraan untuk masalah optimasi dan pencarian. Algoritma genetika adalah kelas khusus dari algoritma evolusi yang menggunakan teknik yang terinspirasi oleh biologi evolusi seperti pewarisan, mutasi, seleksi alam dan rekombinasi (atau persilangan). Algoritma genetika pertama kali dikembangkan pada tahun 1970an oleh John Holland di New York, AS. Dia, murid-muridnya dan rekan-rekannya menerbitkan sebuah buku pada tahun 1975 berjudul “Adaptasi dalam Sistem Alam dan Buatan.”

Algoritme genetik biasanya diimplementasikan sebagai simulasi komputer di mana populasi representasi abstrak (disebut kromosom) dari solusi potensial (disebut unit) terhadap masalah optimasi berkembang menuju solusi yang lebih baik. Secara tradisional, solusi dalam format biner direpresentasikan sebagai string "0" dan "1", meskipun berbagai pengkodean juga dimungkinkan.Evolusi dimulai dari sebuah populasi individual acak yang lengkap dan terjadi dalam generasi-generasi.

Dalam tiap generasi, kemampuan keseluruhan populasi dievaluasi, kemudian multiple individuals dipilih dari populasi sekarang (current) tersebut secara stochastic (berdasarkan kemampuan mereka), lalu dimodifikasi (melalui mutasi atau rekombinasi) menjadi bentuk populasi baru yang menjadi populasi sekarang (current) pada iterasi berikutnya dari algoritme.

Prosedur Algoritma Genetik

Algoritma genetika umum memerlukan definisi dua hal: (1) representasi genetik dari solusi, (2) fungsi kemampuan untuk mengevaluasinya.

Representasi defaultnya adalah array bit. Dengan cara yang sama, Anda dapat menggunakan array dengan tipe dan struktur lain. Alasan utama keakuratan representasi genetik ini adalah karena bagian-bagiannya dapat dengan mudah disusun karena ukurannya yang konstan, sehingga memudahkan operasi persilangan yang sederhana. Representasi panjang variabel juga digunakan, namun dalam kasus ini implementasi crossover lebih kompleks.Representasi pohon dipelajari dalam pemrograman genetik dan representasi bebas di HBGA.

Fungsi kapasitas ditentukan berdasarkan representasi genetik dan mengukur kualitas solusi yang disajikan. Fungsi kapasitas selalu bergantung pada masalahnya. Misalnya saja jika kita ingin memaksimalkan jumlah barang (benda) yang dapat ditampung dalam tas ransel dengan kapasitas tetap tertentu. Representasi solusinya dapat berupa bit array, dimana setiap bit merepresentasikan objek yang berbeda dan nilai bit (0 atau 1) menggambarkan apakah objek tersebut berada di dalam backpack atau tidak.Tidak semua representasi seperti itu berhasil karena ukuran benda tersebut mungkin melebihi kapasitas ransel.

Kapasitas solusi, jika direpresentasikan dengan benar, adalah jumlah dari nilai semua benda di dalam ransel, jika tidak maka akan menjadi 0. Dalam beberapa soal, mendefinisikan simbol kapasitas sulit atau tidak mungkin, sehingga IGA digunakan dalam kasus ini. .Setelah representasi genetik dan fungsi kebugaran ditentukan, algoritme genetika memproses inisialisasi acak populasi pada resolusi dan memperbaikinya dengan menerapkan operator mutasi, persilangan, dan seleksi berulang kali.

Secara sederhana, algoritme umum dari algoritme genetik ini dapat dirumuskan menjadi beberapa langkah, yaitu:

1. Membentuk suatu populasi individual dengan keadaan acak
2. Mengevaluasi kecocokan setiap individual keadaan dengan hasil yang diinginkan
3. Memilih individual dengan kecocokan yang tertinggi
4. Bereproduksi, mengadakan persilangan antar individual terpilih diselingi mutasi
5. Mengulangi langkah 2 - 4 sampai ditemukan individual dengan hasil yang diinginkan

Sumber: id.wikipedia.org

Heuristika

Heuristik adalah seni dan sains yang berkaitan dengan penemuan, berasal dari kata dasar yang sama dengan “eureka”, yang berarti “menemukan”. Heuristik dalam konteks pemecahan masalah merupakan suatu cara membimbing pemikiran seseorang untuk memecahkan suatu masalah hingga berhasil diselesaikan. Meskipun proses heuristik ini mungkin tidak selalu memberikan hasil yang diinginkan atau bahkan menimbulkan masalah baru, namun sangat berharga dalam memperkaya proses berpikir. Heuristik yang baik dapat secara signifikan mengurangi waktu yang dibutuhkan untuk menyelesaikan suatu masalah dengan menghilangkan kebutuhan untuk mempertimbangkan kemungkinan atau hubungan yang mungkin tidak relevan ketika masalah tersebut muncul.

Gambaran Umum

Heuristik adalah strategi yang didasarkan pada pengalaman sebelumnya dengan masalah serupa. Bergantung pada informasi yang dapat diakses, heuristik digunakan untuk memandu solusi masalah abstrak manusia dan mesin. Salah satu heuristik paling dasar adalah trial and error, yang diterapkan dari permasalahan sederhana hingga penyelesaian variabel dalam permasalahan aljabar. Dalam matematika, heuristik mencakup penggunaan representasi visual, asumsi tambahan, penalaran maju/mundur, dan penyederhanaan. George Pólya, dalam bukunya “How to Solve It,” menyarankan beberapa heuristik umum, seperti menggambar ketika sulit untuk menyelesaikannya. memahami masalah, menggunakan solusi yang diasumsikan untuk mengeksplorasi ide, mempelajari contoh-contoh konkret ketika masalah bersifat abstrak, dan menangani solusi umum. Masalah pertama, mengikuti paradoks penemu, yang menyatakan bahwa perencanaan yang lebih ambisius mempunyai peluang keberhasilan yang lebih besar.

Sejarah

Heuristika sebagai prosedur preskriptif

Metode heuristik pertama kali muncul dalam filsafat dan matematika abad ke-13 bersama Raimundus Lullus, yang mengembangkan pendekatan skolastik Aristoteles untuk memecahkan masalah menggunakan algoritma tradisional. Pada abad ke-17, Gottfried Wilhelm Leibniz mencoba mengembangkan algoritma universal untuk mewakili semua masalah yang mungkin terjadi. René Descartes merumuskan aturan sederhana untuk menyelesaikan masalah dengan memusatkan perhatian pada aspek-aspek yang relevan. Pada tahun 1, Bernard Bolzano mengembangkan heuristik untuk agensi epistemik, menyadari bahwa heuristik mencakup prosedur umum dan tidak jelas untuk mendorong pemikiran kreatif.

George Pólya memberikan apresiasi yang lebih besar terhadap heuristik dalam matematika modern pada abad ke-20, menekankan pencarian analogi, reduksi masalah, serta dekomposisi dan rekombinasi masalah sebagai pendekatan yang efektif.Prinsip kepuasan dalam heuristik keputusan, yang dikembangkan oleh Herbert A. Simon, memperkenalkan konsep bahwa pengambil keputusan sering kali memilih solusi yang “cukup baik” yang memenuhi persyaratan minimum. Pada tahun 1970an dan 1980an, Amos Tversky dan Daniel Kahneman memperluas studi heuristik dalam pengambilan keputusan manusia dengan mengakui bahwa pengambil keputusan sering bertindak dengan cara yang rasional dan menciptakan istilah "memuaskan" untuk menggambarkan situasi di mana solusi dianggap memadai. diketahui meskipun belum optimal.

Heuristika sebagai strategi model komputasi

Pada tahun 1970-an, kemunculan komputer sebagai alat komputasi dan metafora pikiran memicu upaya untuk mensimulasikan perilaku cerdas pada mesin, khususnya dalam pemecahan masalah komputasi. Dalam konteks ini, beberapa heuristik diidentifikasi, dengan penelitian sistematis yang mengklasifikasikan aturan keputusan berdasarkan dimensi tertentu. Gigerenzer (2001) memperkenalkan “Adaptive Toolbox,” yang menggambarkan heuristik melalui tiga modul: aturan pencarian, aturan penghentian, dan aturan keputusan.Prinsip dasar model komputasi disesuaikan dengan tugas, situasi dan keputusan pembuatnya serta menggabungkan dua pendekatan dari literatur dalam bentuk formal. Model tersebut membentuk komponen dasar berbagai heuristik yang berkaitan dengan peralatan adaptif dan klasifikasi Svenson (1979).Konsep baru heuristik Gigerenzer (2001) dalam strategi ekologi rasional menantang keyakinan bahwa heuristik selalu memberikan hasil terbaik kedua dan bahwa optimalisasi selalu lebih baik daripada perangkat adaptif.

Penilaian probabilitas dan frekuensi

Strategi pemecahan masalah heuristik dapat dibagi menjadi empat bagian yang mempengaruhi penilaian probabilitas dan frekuensi. Pertama, heuristik ketersediaan didasarkan pada gagasan bahwa sesuatu yang mudah diingat dianggap lebih penting daripada solusi alternatif. Kedua, heuristik keterwakilan digunakan untuk menilai probabilitas subjektif dengan mempertimbangkan derajat kemiripan suatu peristiwa terhadap fitur-fitur penting atau fitur-fitur yang menonjol. Ketiga, heuristik penahan dan penyesuaianmemengaruhi penilaian probabilitas intuitif dengan memulai dari titik referensi tertentu dan membuat penyesuaian berdasarkan informasi tambahan. Terakhir, heuristik keakraban mengevaluasi peristiwa sebagai sesuatu yang lebih umum atau penting karena peristiwa tersebut lebih familier dalam ingatan dan menggunakan pengalaman masa lalu sebagai kerangka acuan untuk berperilaku dalam situasi baru dan familier.

Kecerdasan Buatan

Saat mencari ruang solusi, heuristik dapat digunakan dalam sistem kecerdasan buatan. Heuristik ini diperoleh dengan menggunakan berbagai fungsi yang dimasukkan ke dalam sistem oleh perancang atau dengan menyesuaikan bobot cabang, yang ditentukan oleh probabilitas setiap cabang mengarah ke node target.

Kritik dan Kontroversi

Konsep heuristik menuai kritik dan kontroversi. Kritik terhadap Kita Tidak Bisa Sebodoh Itu berpendapat bahwa rata-rata orang memiliki sedikit kemampuan untuk membuat penilaian efektif berdasarkan data.

Sumber: id.wikipedia.org

Dinamika Sistem

Dinamika sistem (dikenal dalam bahasa Inggris sebagai System Dynamics) adalah metode pemodelan yang diperkenalkan oleh Jay Forrester pada tahun 1950-an dan dikembangkan di Massachusetts Institute of Technology, AS. Tujuan utama dari metode ini adalah untuk mempelajari tren dinamis dalam sistem yang kompleks, yaitu pola perilaku yang berkembang seiring waktu. Paradigma dinamika sistem mengasumsikan bahwa pola dinamika berkelanjutan dalam sistem kompleks apa pun muncul daristruktur sebab akibat yang membentuk sistem tersebut. Oleh karena itu, model dinamika sistem masuk dalam kategori model matematika kausal atau teori sebab-akibat.

Prinsip-prinsip

Metodologi dinamika sistem pada dasarnya menggunakan hubungan sebab akibat dalam membangun model sistem yang kompleks sebagai dasar untuk mengenali dan memahami perilaku dinamis sistem. Dengan kata lain, penggunaan metodologi dinamika sistem lebih fokus pada tujuan meningkatkan pemahaman kita tentang bagaimana perilaku sistem muncul dari strukturnya. Permasalahan yang dapat dimodelkan secara memadai dengan menggunakan metodologi dinamika sistem adalah permasalahan yang bersifat dinamis (berubah terhadap waktu) dan struktur fenomenanya mengandung paling sedikit satu struktur umpan- balik (feedback structure).

Prinsip-prinsip untuk menciptakan model dinamis, seperti yang dijelaskan oleh Sterman (1981), meliputi pemisahan antara keadaan yang diinginkan dan keadaan sebenarnya, representasi struktur aliran dan keberadaan nyata, pemisahan aliran konseptual, penggunaan informasi yang diberikan kepada aktor dalam sistem. tersedia, kesesuaian struktur aturan pengambilan keputusan dengan praktik pengelolaan dan keberlanjutan model dalam kondisi ekstrim.

Sedangkan untuk ketahanan suatu model, menurut Sterman, perlu dilakukan sejumlah pengujian agar pada gilirannya kepercayaan pengguna terhadap kemampuan model dalam mengekspresikan sistem yang diwakilinya meningkat. Keyakinan inilah yang menjadi dasar validitas model. Setelah validitas model tercapai, simulasi dapat digunakan untuk merancang kebijakan yang efektif.

Struktur dan Hubungan Dalam Model

Model dinamika sistem muncul karena adanya hubungan sebab-akibat yang mempengaruhi struktur di dalamnya, baik secara langsung antara dua struktur maupun akibat dari berbagai hubungan yang terjadi pada struktur yang berbeda, sehingga membentuk suatu putaran umpan balik (causal loop). Struktur umpan balik ini adalah blok penyusun model, yang diekspresikan melalui hubungan sebab-akibat loop tertutup dari variabel.

Terdapat dua jenis hubungan sebab akibat dalam sistem, yaitu hubungan sebab akibat positif dan hubungan sebab akibat negatif. Selain itu, ada dua jenis umpan balik, yaitu umpan balik positif terkait pertumbuhan (growth) dan umpan balik negatif terkait pencapaian tujuan (goalpurse).

Saat merepresentasikan aktivitas dalam putaran umpan balik, dua jenis variabel utama digunakan: stok dan aliran (juga disebut level dan laju atau stok dan aliran). Inventaris mewakili keadaan sistem pada setiap saat.Dalam teknologi, sistem inventaris lebih dikenal dengan istilah sistem keadaan variabel. Persediaan terakumulasi dalam sistem. Persamaan tarif variabel adalah struktur kebijakan yang menjelaskan mengapa dan bagaimana suatu keputusan dibuat berdasarkan informasi yang tersedia dalam sistem.Arus adalah satu-satunya variabel dalam model yang dapat mempengaruhi saham.

Selain variabel stok dan aliran, terdapat variabel pembantu lainnya, konstanta dan penundaan dalam pemodelan dinamika sistem. Variabel bantu adalah variabel yang dapat berubah seiring berjalannya waktu. Perubahan tersebut dapat disebabkan oleh hubungan sebab akibat antar variabel dalam model atau oleh variabel eksternal yang independen. Konstanta adalah variabel dengan nilai tetap yang tidak berubah seiring waktu. Sedangkan lag merupakan variabel waktu dalam perubahan perilaku yang tidak terjadi dengan segera (tertunda) pada proses yang terjadi pada hubungan antar struktur dan mempengaruhi perilaku model.

Penggunaan

Awalnya Forrester menerapkan metodologi systemdynamics untuk menyelesaikan permasalahan di industri (bisnis). Model dinamika sistem pada awalnya membahas masalah manajemen umum seperti fluktuasi persediaan, ketidakstabilan tenaga kerja, dan penurunan pangsa pasar perusahaan (lihat Forrester, 1961). Perkembangannya terus meningkat sejak penggunaannya dalam permasalahan sistem sosial yang sangat berbeda, dilakukan dan digunakan olehpemegang polis.

Pemanfaatan Perangkat Lunak

Model dinamika sistem biasanya dibuat menggunakan perangkat lunak yang dikembangkan secara khusus. Perangkat lunak ini mencakup Powersim, Vensim, Stella dan Dynamo. Perangkat lunak ini digunakan untuk membuat model secara grafis dengan simbol variabel dan hubungannya. Namun, tidak menutup kemungkinan bahwa perangkat lunak yang mampu memproses operasi matematika tipe spreadsheet, seperti Microsoft Excel atau Lotus, juga dapat digunakan untuk memodelkan dinamika sistem.

Perkembangan Dinamika Sistem di Indonesia

Di Indonesia, Institut Teknologi Bandung (ITB) merupakan salah satu lembaga pendidikan yang mengajarkan dinamika sistem. Di ITB, dinamika sistem diajarkan melalui mata kuliah pemodelan pada program Magister Studi Pembangunan (S2). Selain itu, ITB juga menawarkan kesempatan mempelajari dinamika sistem melalui kursus. Dalam bidang ilmu transportasi, dinamika sistem diajarkan melalui mata kuliah Pemodelan Transportasi Laut di Jurusan Transportasi Laut (S1), Sistem Informasi (S1, Magister, PhD)bidang pemodelan dan simulasi dari tahun 2006 serta teknik sistem dan industri. . di lembaga pendidikan Institut Teknologi Sepuluh Nopember (ITS) dan pada mata kuliah Pemodelan dan Sistem Dinamis pada jurusan Sistem Informasi Bisnis (SIB) Institut Sains dan Teknologi Terpadu (ISTTS) Surabaya sejak tahun 2021.

Khusus Institut Teknologi Sepuluh Nopember (ITS), sejak tahun 2020, Departemen Kajian Sistem Informasi mempunyai guru besar bidang pemodelan sistem dinamik bernama Prof.Erma Suryani, ST, MT, Ph.D. yang dikukuhkan pada 14 April 2021.

Selain itu, terdapat lembaga swasta yang mengajarkan dan mempopulerkan dinamika sistem, yaitu System Dynamics Center (SDC) yang bekerja sama dengan universitas-universitas di Indonesia untuk mengembangkan dan mempopulerkan pemodelan dinamika sistem, dengan tujuan memberikan Indonesia skenario terbaik untuk membangun .

Sumber: id.wikipedia.org

Dinamika sistem

Dinamika sistem (SD) adalah pendekatan untuk memahami perilaku nonlinear dari sistem yang kompleks dari waktu ke waktu menggunakan stok, aliran, loop umpan balik internal, fungsi tabel, dan penundaan waktu.

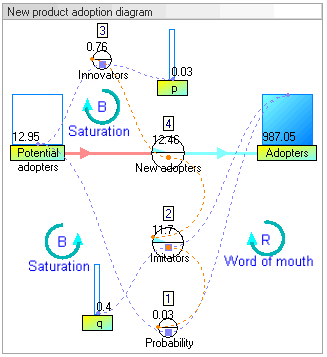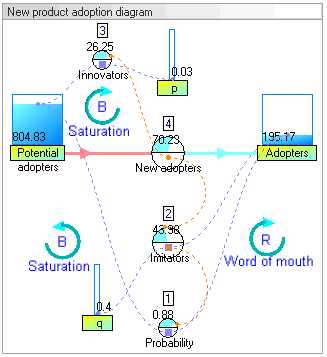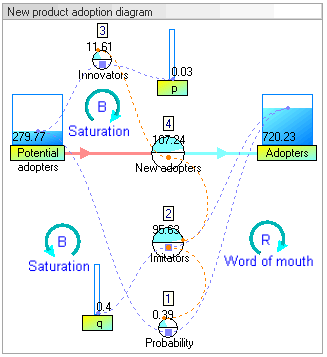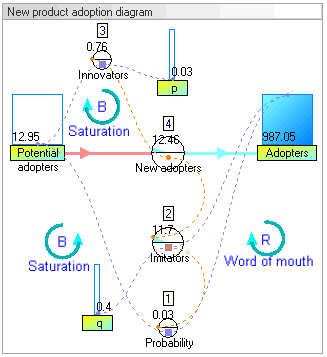
Stok dinamis dan diagram alir model Adopsi produk baru (model dari artikel oleh John Sterman 2001 - True Software)

Ringkasan

Dinamika sistem adalah pendekatan matematis untuk memodelkan dan memahami masalah kompleks dengan mempertimbangkan interaksi antar variabel dari waktu ke waktu. Ini dikembangkan pada tahun 1950an dan digunakan baik di sektor publik maupun swasta. Perangkat lunak ini, dengan antarmuka pengguna grafis (GUI), menjadi lebih ramah pengguna pada tahun 1990an. Model dinamika sistem mengatasi masalah konkurensi dengan memperbarui variabel pada interval waktu kecil menggunakan umpan balik positif dan negatif serta penundaan waktu.

Waktu. Model yang terkenal termasuk The Limits to Growth tahun 1972, yang memperkirakan keruntuhan ekonomi abad ke-21 karena pertumbuhan eksponensial dan terbatasnya sumber daya.Dinamika sistem adalah cabang teori sistem yang mengakui bahwa struktur sistem melibatkan hubungan melingkar, penundaan waktu, dan kompleksitas yang mempengaruhi perilaku secara keseluruhan. Contoh penerapannya termasuk teori chaos dan dinamika sosial. Ditekankan bahwa perilaku umum tidak selalu dapat dijelaskan oleh perilaku individu dalam sistem.

Sejarah

Dinamika sistem, ditemukan pada tahun 1950an oleh profesor MIT Jay Forrester, pada awalnya bertujuan untuk memahami masalah mendasar dalam manajemen bisnis. Menggunakan observasi dari siklus tiga tahun di pabrik General Electric (GE), Forrester mengembangkan konsep dinamika sistem melalui simulasi manual. Pada akhir 1950-an, Forrester dan tim mahasiswanya beralih ke pemodelan komputer formal menggunakan bahasa seperti SIMPLE dan DYNAMO. “Dinamika Industri,” buku pertama Forrester yang diterbitkan pada tahun 1961, menjadi buku klasik di bidangnya.

Awalnya digunakan untuk masalah perusahaan, dinamika sistem diperluas ke aplikasi non-perusahaan setelah buku Urban Dynamics karya Collins-Forrester Collaboration pada tahun 1968.Usulan kedua muncul ketika Forrester diundang oleh Club of Rome pada tahun 1970 untuk mengatasi krisis global. Forrester menciptakan model dinamika sistem pertama untuk sistem sosial ekonomi global yang disebut WORLD1, yang kemudian diperbarui menjadi WORLD2. Pada tahun 1972, Forrester menerbitkan World Dynamics, yang memperkenalkan dinamika sistem ke dalam domain global untuk memecahkan masalah-masalah manusia yang tersebar luas.

Topik dalam dinamika sistem

Elemen utama diagram dinamika sistem adalah umpan balik, akumulasi aliran ke inventaris, dan waktu tunda.Sebagai contoh pemanfaatan dinamika sistem, pertimbangkan sebuah organisasi yang berencana memperkenalkan produk konsumen yang baru, tahan lama, dan inovatif. Perusahaan perlu memahami kemungkinan dinamika pasar untuk merancang rencana pemasaran dan produksi.

Causal loop diagrams (Diagram lingkaran sebab akibat)

Dalam metodologi dinamika sistem, suatu masalah atau sistem (misalnya ekosistem, sistem politik, atau sistem mekanis) dapat direpresentasikan sebagai diagram lingkaran sebab akibat. Diagram lingkaran sebab akibat adalah peta sederhana suatu sistem dengan seluruh komponennya dan interaksinya. Dengan menangkap interaksi dan putaran umpan balik berikutnya (lihat gambar di bawah), diagram lingkaran sebab akibat mengungkapkan struktur sistem. Dengan memahami struktur suatu sistem, dimungkinkan untuk menentukan perilaku sistemselama periode waktu tertentu.

Diagram lingkaran sebab-akibat dari pengenalan produk baru mungkin terlihat sebagai berikut:

Gambar: Diagram lingkaran kausal dari model adopsi produk baru

Diagram mengilustrasikan dua putaran umpan balik dalam suatu sistem. Lingkaran penguatan positif di sebelah kanan (R) menunjukkan bahwa semakin banyak orang mengadopsi produk baru, semakin kuat pengaruh promosi dari mulut ke mulut, yang menyebabkan peningkatan rekomendasi, demo, dan ulasan produk. Siklus ini berpotensi menghasilkan pertumbuhan penjualan lebih lanjut.Di sebelah kiri ada putaran umpan balik kedua (B), yaitu penguatan negatif atau “keseimbangan”. Pertumbuhan tidak dapat berlanjut tanpa batas waktu karena semakin banyak orang yang mengadopsi, semakin sedikit potensi yang mengadopsinya.Kedua loop ini bekerja sama dan kekuatannya dapat bervariasi pada waktu yang berbeda. Meskipun pada awalnya mungkin terjadi peningkatan penjualan, lama kelamaan mungkin terjadi penurunan. Namun, representasi visual dalam diagram lingkaran sebab akibat tidak cukup untuk menentukan perilaku sistem secara keseluruhan.

Stock and flow diagrams (Diagram stok dan flow)

Diagram lingkaran sebab akibat membantu memvisualisasikan dan menganalisis secara kualitatif struktur dan perilaku sistem. Untuk analisis kuantitatif yang lebih detail, diagram causal loop diubah menjadi diagram inventaris dan diagram alir. Model stok dan aliran membantu memeriksa dan menganalisis sistem secara kuantitatif. Model-model ini biasanya dibuat dan disimulasikan menggunakan perangkat lunak komputer.“Saham” adalah istilah untuk setiap unit yang terakumulasi atau berkurang seiring berjalannya waktu. Arus adalah laju perubahan saham.

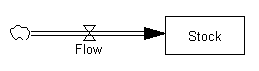
Gambar: Aliran adalah tingkat akumulasi stok

Dalam contoh kami, ada dua stok: Pengadopsi potensial dan Pengadopsi. Ada satu aliran: Pengadopsi baru. Untuk setiap pengadopsi baru, stok pengadopsi potensial berkurang satu, dan stok pengadopsi bertambah satu.

Gambar: Diagram stok dan aliran model adopsi produk baru

Persamaan

Kekuatan nyata dari dinamika sistem dimanfaatkan melalui simulasi. Meskipun dimungkinkan untuk melakukan pemodelan dalam spreadsheet, ada berbagai paket perangkat lunak yang telah dioptimalkan untuk ini.

Langkah-langkah yang dilakukan dalam simulasi adalah:

• Tentukan batas masalah
• Identifikasi stok dan arus paling penting yang mengubah tingkat stok ini
• Mengidentifikasi sumber informasi yang berdampak pada arus
• Identifikasi loop umpan balik utama
• Gambarlah diagram lingkaran sebab akibat yang menghubungkan stok, aliran, dan sumber informasi
• Tuliskan persamaan yang menentukan aliran
• Perkirakan parameter dan kondisi awal. 
• Simulasikan model dan analisis hasilnya.

Dalam contoh ini, persamaan yang mengubah dua stok melalui aliran adalah:

Persamaan dalam waktu diskrit

Daftar semua persamaan dalam waktu diskrit, dalam urutan pelaksanaannya di setiap tahun, untuk tahun 1 sampai 15 :

Hasil simulasi dinamis
Hasil simulasi dinamis menunjukkan bahwa perilaku sistem akan memiliki pertumbuhan pengadopsi yang mengikuti bentuk kurva-s klasik.
Peningkatan pengadopsi sangat lambat pada awalnya, kemudian pertumbuhan eksponensial untuk suatu periode, akhirnya diikuti oleh kejenuhan.

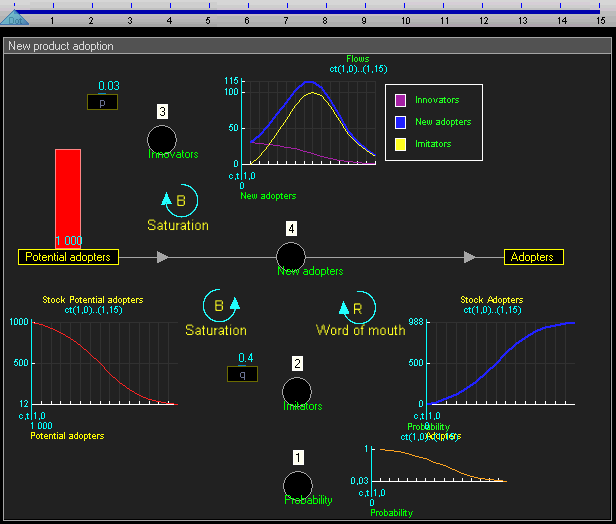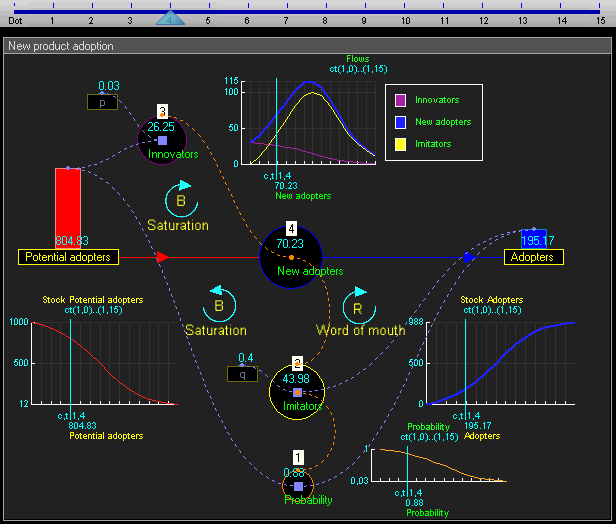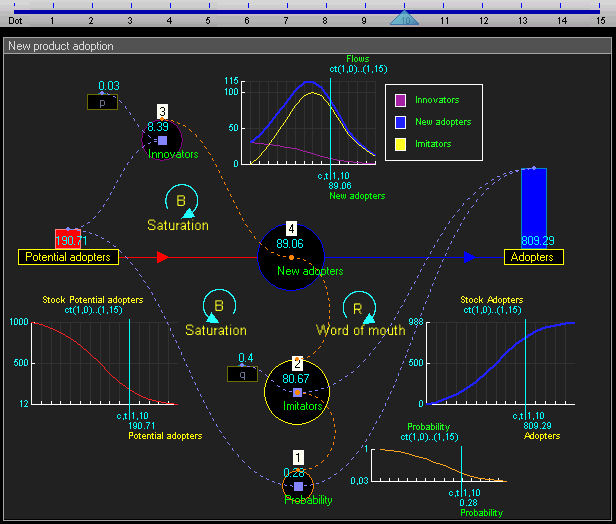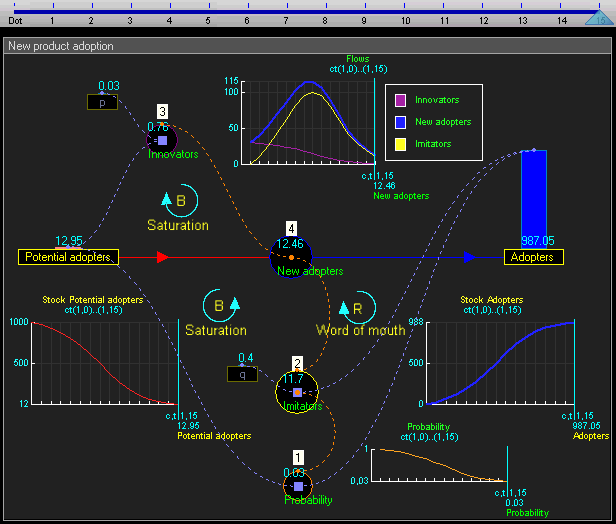
Gambar: Stok dinamis dan diagram alir model adopsi produk baru

Gambar: Nilai stok dan aliran selama bertahun-tahun = 0 hingga 15

Persamaan dalam waktu kontinu

Untuk mendapatkan nilai menengah dan akurasi yang lebih baik, model dapat berjalan dalam waktu yang berkelanjutan: kita mengalikan jumlah unit waktu dan membagi nilai secara proporsional yang mengubah tingkat stok. Dalam contoh ini kita mengalikan 15 tahun dengan 4 untuk mendapatkan 60 kuartal, dan kita membagi nilai arus dengan 4.
Membagi nilai adalah yang paling sederhana dengan metode Euler, tetapi metode lain dapat digunakan sebagai gantinya, seperti metode Runge–Kutta.

Daftar persamaan dalam waktu kontinu untuk trimester = 1 sampai 60 :

Mereka adalah persamaan yang sama seperti pada bagian Persamaan waktu diskrit di atas, kecuali persamaan 4.1 dan 4.2 diganti dengan yang berikut:

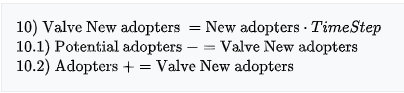
Dalam diagram stok dan aliran di bawah ini, aliran perantara 'Valve New adopters' menghitung persamaan:

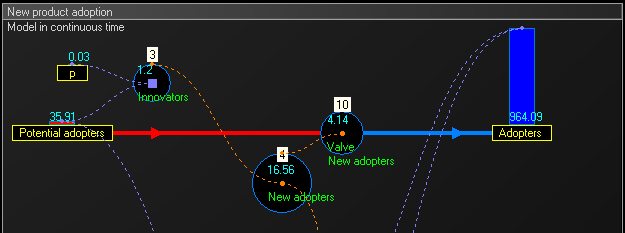
Gambar: Stok dinamis dan diagram alir model adopsi produk baru dalam waktu kontinu

Aplikasi

Dinamika sistem memiliki beragam aplikasi di berbagai bidang seperti: Misalnya sistem kependudukan, pertanian, ekologi dan ekonomi yang seringkali saling berinteraksi. Dalam manajemen “terbelakang”, dinamika sistem digunakan sebagai alat untuk mengajarkan refleks berpikir sistem, menganalisis asumsi dan model mental, memperoleh wawasan kualitatif tentang cara kerja sistem, dan mengenali arketipe sistem yang tidak berfungsi.Penggunaan perangkat lunak memungkinkan simulasi model dinamika sistem, memungkinkan pengujian bagaimana-jika kebijakan tertentu untuk memahami perubahan dalam sistem dari waktu ke waktu. Dinamika sistem, mirip dengan pemikiran sistem, menciptakan diagram lingkaran sebab akibat, namun melangkah lebih jauh dan menggunakan simulasi untuk menguji perilaku sistem dan dampak dari kebijakan alternatif.Dinamika sistem juga digunakan dalam studi ketergantungan sumber daya dan masalah pengembangan produk.Minsky, pendekatan makroekonomi yang dikembangkan oleh ekonom Steve Keen, menggunakan dinamika sistem untuk memodelkan perilaku perekonomian global dari periode stabilitas hingga krisis keuangan yang tidak terduga pada tahun 2007-2008.

Contoh: Pertumbuhan dan penurunan perusahaan

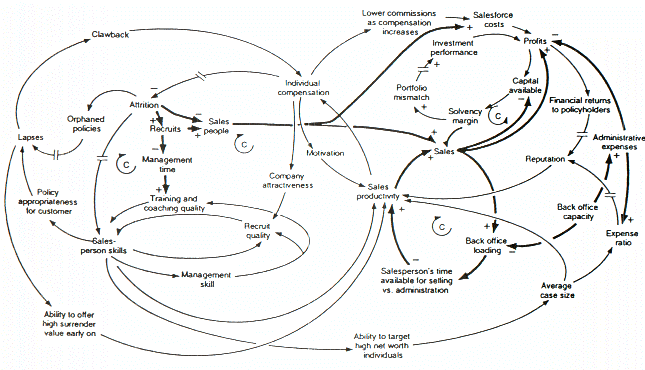
Gambar: Causal loop diagram dari model yang memeriksa pertumbuhan atau penurunan perusahaan asuransi jiwa

Gambar di atas adalah diagram lingkaran sebab akibat dari model dinamika sistem yang dibuat untuk menganalisis pertumbuhan atau penurunan perusahaan asuransi jiwa di Inggris. Fitur penting dari diagram ini mencakup putaran umpan balik negatif yang disebut putaran balik (C), penggunaan batang ganda untuk menunjukkan penundaan yang signifikan antara sebab dan akibat, garis yang lebih tebal untuk mengidentifikasi putaran umpan balik dan koneksi untuk disorot, dan tingkat kesulitanuntuk pengambil keputusan dapat secara dinamis Memahami perilaku hanya dengan menggunakan gambar. Konvensi diagram dinamika sistem umumnya digunakan untuk menyampaikan informasi ini.

Contoh: gerak piston

1. Tujuan: mempelajari sistem batang penghubung engkol.
Kami ingin memodelkan sistem batang penghubung engkol melalui model sistem dinamis. Dua deskripsi lengkap yang berbeda dari sistem fisik dengan sistem persamaan terkait dapat ditemukan di sini (dalam bahasa Inggris) dan di sini (dalam bahasa Prancis); mereka memberikan hasil yang sama. Dalam contoh ini, engkol, dengan jari-jari variabel dan frekuensi sudut, akan menggerakkan piston dengan panjang batang penghubung variabel.

2. Pemodelan dinamis sistem: sistem sekarang dimodelkan, menurut logika dinamis sistem stok dan aliran.
Gambar di bawah ini menunjukkan diagram stok dan aliran

Gambar: Diagram stok dan aliran untuk sistem batang penghubung engkol

3. Simulasi: perilaku sistem dinamis batang penghubung engkol kemudian dapat disimulasikan.
Gambar selanjutnya adalah simulasi 3D yang dibuat menggunakan animasi prosedural. Variabel model menganimasikan semua bagian animasi ini: engkol, radius, frekuensi sudut, panjang batang, dan posisi piston.

Gambar: Animasi prosedural 3D dari sistem batang penghubung engkol yang dimodelkan 

Disadur dari : en.wikipedia.org

Teori Antrian

Teori antrian merupakan kajian matematis terkait antrian yang menciptakan model untuk memprediksi panjang antrian dan waktu tunggu. Sebagai salah satu cabang riset operasi, teori antrian banyak digunakan untuk mengambil keputusan bisnis mengenai sumber daya yang dibutuhkan untuk menyediakan layanan. Teori antrian yang ditemukan oleh Agner Krarup Erlang didasarkan pada model sistem panggilan masuk di Copenhagen Telephone Exchange Company. Penerapan ide-ide ini meluas ke berbagai bidang, termasuk telekomunikasi, teknik transportasi, ilmu komputer, manajemen proyek dan khususnya teknik industri, yang dapat diterapkan pada desain pabrik, pertokoan, perkantoran, dan rumah sakit.

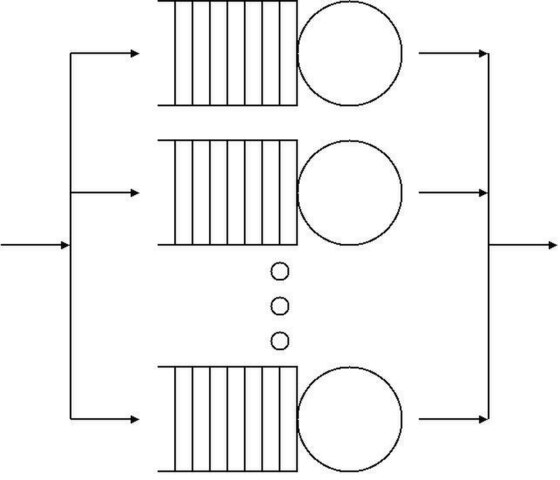
Jaringan antrian adalah sistem di mana antrian individu dihubungkan oleh jaringan perutean. Pada gambar ini, server diwakili oleh lingkaran, antrian diwakili oleh serangkaian persegi panjang, dan jaringan routing diwakili oleh panah. Ketika mempelajari jaringan antrian, seseorang biasanya mencoba untuk mencapai distribusi keseimbangan jaringan, meskipun mempelajari keadaan transisi sangat sederhana dalam banyak penerapan.

Node antrian tunggal
Node antrian atau simpul antrian hampir dapat dianggap sebagai kotak hitam. Pekerjaan (juga dikenal sebagai klien atau permintaan tergantung pada bidangnya) tiba dalam antrean, mungkin menunggu beberapa saat, memerlukan waktu untuk diproses, dan kemudian meninggalkan antrean.

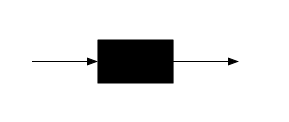
Sebuah kotak hitam (blackbox). Pekerjaan datang ke, dan berangkat dari, antrian.

Namun, node akhir bukanlah kotak hitam murni karena diperlukan beberapa informasi tentang bagian dalam node akhir. Antrian memiliki satu atau lebih server dan masing-masing server dapat dipasangkan dengan pekerjaan masuk. Ketika suatu pekerjaan selesai dan keluar, server tersebut dapat kembali berkomunikasi dengan semua pekerjaan masuk lainnya.

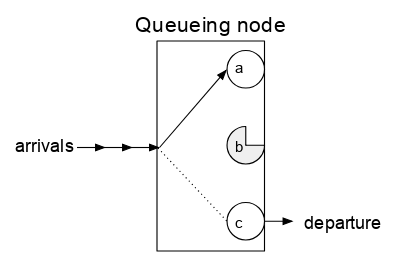
Node antrian dengan 3 server. Server a sedang down sehingga data yang masuk diteruskan untuk diproses. Server b sedang sibuk dan perlu beberapa saat untuk menyelesaikan tugasnya. Server c baru saja selesai memproses pekerjaan dan kemudian menerima pekerjaan masuk.

Analogi yang umum digunakan adalah analogi seorang kasir di supermarket.(Ada model lain, tapi model ini sering ditemukan dalam literatur). Pelanggan datang, diproses oleh kasir dan pergi lagi. Setiap ATM memproses satu pelanggan pada satu waktu dan oleh karena itu merupakan node antrian dengan satu server. Pengaturan dimana pelanggan segera pergi jika kasir sedang sibuk ketika pelanggan datang disebut antrian tanpa buffer (atau non-menunggu). Konfigurasi dengan ruang tunggu hingga n klien disebut antrian dengan buffer berukuran n.

Sejarah

Pada tahun 1909, Agner Krarup Erlang, seorang insinyur Denmark di bursa telepon Kopenhagen, memulai teori antrian dengan memodelkan jumlah panggilan telepon masuk menggunakan proses Poisson dan pada tahun 1917 mengembangkan antrian M/D/1 dan M/D/k- Antrian terpecahkan. model pada tahun 1920. Notasi Kendall diperkenalkan pada tahun 1953 oleh David George Kendall, yang kemudian memecahkan antrian GI/M/k. Felix Pollaczek dan Aleksandr Khinchine mengembangkan rumus Pollaczek-Khinchine untuk antrian M/G/1 pada tahun 1930.Pada tahun 1957, Pollaczek mempelajari GI/G/1 dan John Kingman mengembangkan rumus untuk waktu tunggu rata-rata dalam antrian G/G/ 1., yang dikenal sebagai rumus Kingman. Leonard Kleinrock menerapkan teori antrian pada perpindahan pesan dan paket pada tahun 1960an dan 1970an dan menganjurkan penggunaan perpindahan paket di ARPANET.Metode matriks geometris dan analisis matriks memungkinkan pertimbangan antrian dengan distribusi kedatangan dan distribusi waktu pelayanan. Sistem orbit berpasangan penting dalam teori antrian, khususnya dalam jaringan nirkabel dan pemrosesan sinyal. Penerapan teori antrian modern mencakup pengembangan produk dengan keberadaan spatiotemporal, serta pertanyaan seperti metrik kinerja untuk antrian M/G/K, yang masih terbuka.

Disiplin layanan

.

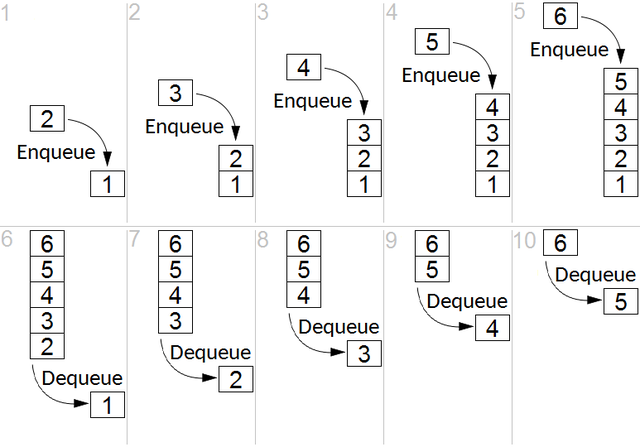Contoh antrian masuk pertama keluar pertama (FIFO).
Beberapa kebijakan penjadwalan di node akhir meliputi: First in, First out (FCFS), dimana pelanggan dilayani berdasarkan siapa cepat dia dapat; “Masuk terakhir, keluar pertama”, di mana pelanggan dilayani satu per satu dan pelanggan dengan waktu tunggu tersingkat dilayani terlebih dahulu (juga dikenal sebagai “penumpukan”); Pemroses bersama dengan kapasitas layanan dibagi rata antar klien berdasarkan prioritas, dengan klien berprioritas tinggi dilayani terlebih dahulu () (dengan jenis antrian prioritas non-preemptive dan preemptive); pekerjaan terpendek terlebih dahulu, dengan tugas dengan waktu pelaksanaan terpendek diselesaikan terlebih dahulu; pertama pekerjaan persiapan terpendek, dimana pesanan dikirimkan dengan ukuran asli terkecil; Sisa waktu pemrosesan terpendek, dengan pesanan dengan sisa pemrosesan paling sedikit harus diselesaikan terlebih dahulu.Selain itu, terdapat berbagai model instalasi pelayanan, seperti: Misalnya, satu server, beberapa server paralel dengan satu atau beberapa antrian, dan server tidak tepercaya yang gagal setelah proses stokastik diikuti dengan fase konfigurasi di mana server tidak tersedia. . Perilaku menunggu pelanggan meliputi penolakan, ketika pelanggan memilih untuk tidak mengantri jika terlalu panjang; Scramble, dimana pelanggan mengubah antrian jika dirasa akan dilayanilebih cepat; dan penolakan ketika pelanggan meninggalkan antrian jika menunggu terlalu lama untuk dilayani. Pelanggan yang datang dan tidak dilayani baik karena tidak ada buffer antrian atau karena pelanggan menolak disebut juga pengabai, dan rata-rata tingkat pengabaian merupakan parameter penting untuk menggambarkan antrian.

Jaringan antrian (Queueing networks)

Jaringan antrian adalah sistem di mana beberapa antrian dihubungkan melalui perutean pelanggan. Ketika klien menerima layanan pada sebuah node, mereka dapat bergabung dengan node lain untuk mengantri layanan atau meninggalkan jaringan. Dalam jaringan dengan m node, keadaan sistem dapat digambarkan dengan vektor berdimensi m (x1, x2, ...)., xm), dimana xi mewakili jumlah klien pada setiap node. Jaringan antrian nontrivial yang paling sederhana adalah antrian tandem. Jaringan Jackson adalah pencapaian signifikan pertama di bidang ini dan memungkinkan penghitungan metrik rata-rata seperti throughput dan waktu tunggu. Jika jumlah pelanggan dalam jaringan tetap konstan, kita berbicara tentang jaringan tertutup dan distribusi produk stasioner menurut teorema Gordon-Newell. Hasil ini meluas ke jaringan BCMP dan menunjukkan bahwajaringan dengan waktu layanan, rezim, dan rute pelanggan yang sangat umum juga memiliki distribusi bentuk produk yang tetap.Jaringan pelanggan lain juga telah dipelajari, seperti jaringan Kelly, yang memiliki kelas pelanggan berbeda dengan tingkat prioritas berbeda pada node layanan berbeda. Misalnya, jaringan G yang diusulkan oleh Erol Gelenbe pada tahun 1993 tidak mengasumsikan distribusi waktu eksponensial seperti jaringan Jackson klasik.

Algoritma perutean (Routing algorithms)

Dalam jaringan waktu diskrit, di mana jumlah node layanan yang dapat aktif kapan saja terbatas, algoritma penjadwalan bobot maksimum memilih kebijakan layanan untuk memberikan kinerja optimal ketika setiap pekerjaan hanya mengunjungi satu node layanan orang. Dalam kasus yang lebih umum di mana pekerjaan dapat mengunjungi lebih dari satu node, perutean BackPressure memberikan kinerja yang optimal. Perencana jaringan harus memilih algoritma antrian yang berdampak pada karakteristik jaringan
yang lebih besar.

Batas rata-rata bidang

Model medan rata-rata memperhitungkan perilaku pembatas dari ukuran empiris (proporsi ekor di berbagai negara bagian) ketika jumlah ekor m mendekati tak terhingga. Pengaruh antrian lain pada antrian tertentu dalam jaringan diperkirakan dengan persamaan diferensial. Model deterministik menyatu pada distribusi stasioner yang sama dengan model aslinya.

Perkiraan lalu lintas / difusi yang padat

Dalam sistem dengan tingkat hunian tinggi (pemanfaatan mendekati 1), perkiraan lalu lintas yang kuat dapat digunakan untuk memperkirakan proses panjang antrian gerak Brown yang tercermin, proses Ornstein-Uhlenbeck, atau proses difusi yang lebih umum. Jumlah dimensi proses Brown sama dengan jumlah node akhir, dengan difusi terbatas pada speaker non-negatif.

Batas cairan
Model fluida adalah analog deterministik kontinu dari jaringan antrian, yang diperoleh dengan menetapkan batasan ketika menskalakan proses dalam ruang dan waktu dan dengan mempertimbangkan objek yang heterogen. Lintasan berskala ini menyatu dengan persamaan deterministik yang memungkinkan pengujian stabilitas sistem. Diketahui bahwa suatu jaringan antrian dapat stabil namun mempunyai batas fluida yang tidak stabil.

Disadur dari: en.wikipedia.org