Optimasi Stokastik

Metode optimasi stokastik (SO) merupakan metode optimasi yang menghasilkan dan menggunakan variabel acak. Dalam permasalahan stokastik, variabel acak muncul dalam rumusan masalah optimasi itu sendiri dan mencakup fungsi tujuan acak atau batasan acak. Metode optimasi stokastik juga mencakup metode dengan iterasi acak. Beberapa metode optimasi stokastik menggunakan iterasi acak untuk memecahkan masalah stokastik, menggabungkan kedua makna optimasi stokastik. metode optimasi stokastik menggeneralisasi metode deterministik ke masalah deterministik.

Metode fungsi stokastik

Dalam konteks analisis data, terdapat situasi di mana sebagian data masukan bersifat acak, seperti pada bidang estimasi dan kontrol waktu nyata. Selain itu, optimasi berbasis simulasi juga sering melibatkan penggunaan simulasi Monte Carlo sebagai perkiraan sistem sebenarnya. Masalah lain yang dihadapi adalah ketika terdapat kesalahan eksperimental atau kebisingan acak dalam pengukuran kriteria. Dalam kasus-kasus seperti itu, pemahaman bahwa nilai-nilai fungsi dapat terkontaminasi oleh kebisingan acak mendorong pengembangan algoritma yang menggunakan alat inferensi statistik untuk memperkirakan nilai-nilai "sebenarnya" dari fungsi dan/atau membuat keputusan optimal secara statistik terkait langkah-langkah selanjutnya.

Metode yang termasuk dalam kategori ini mencakup berbagai pendekatan seperti pendekatan stokastik (SA) oleh Robbins dan Monro (1951), penurunan gradien stokastik, SA perbedaan hingga oleh Kiefer dan Wolfowitz (1952), gangguan simultan SA oleh Spall (1992), dan optimasi skenario. Keseluruhan, metode-metode ini menyediakan kerangka kerja yang efektif untuk menangani data masukan yang bersifat acak dan kesalahan eksperimental, dengan menggunakan prinsip-prinsip inferensi statistik untuk membuat keputusan yang lebih akurat dan optimal.

Metode pencarian acak

Metode pencarian acak, sering disebut sebagai metaheuristik, memperkenalkan keacakan ke dalam proses pencarian untuk mempercepat kemajuan, terutama ketika kumpulan data terdiri dari pengukuran yang tepat. Keacakan yang diperkenalkan dapat membuat metode ini lebih toleran terhadap kesalahan pemodelan dan menghasilkan keuntungan lain, seperti memperkirakan interval fitur minimum menggunakan statistik nilai ekstrem. Selain itu, keacakan dalam proses pencarian memungkinkan kita untuk keluar dari optimal lokal dan mendekati optimal global, menjadikan prinsip pengacakan ini sebagai cara yang sederhana dan efektif untuk mengembangkan algoritma yang kinerjanya hampir pasti dan konsisten di berbagai kumpulan data dan masalah.

Beberapa metode optimasi stokastik yang menerapkan prinsip pencarian acak antara lain simulasi anil oleh S. Kirkpatrick, CD Gelatt dan MP Vecchi (1983), probabilitas kolektif oleh DH Wolpert, SR Bieniawski dan DG Rajnarayan (2011), dan algoritma genetika oleh Holland (2011). Ada pula metode lain seperti metode cross-entropy dari Rubinstein dan Kroese (2004), random search dari Anatoly Zhigljavsky (1991), dan stochastic tunneling.

Meskipun metode pencarian acak dianggap efektif, beberapa penulis berpendapat bahwa pengacakan hanya dapat meningkatkan algoritma deterministik jika algoritma deterministik dirancang dengan buruk. Ada juga argumen bahwa ketergantungan pada elemen acak dapat menghambat pengembangan komponen deterministik yang lebih cerdas dan unggul. Lebih jauh lagi, menyajikan hasil algoritma optimasi stokastik, misalnya dengan hanya mencantumkan rata-rata atau N run terbaik tanpa menyebutkan distribusi, dapat menghasilkan bias positif terhadap keacakan.

Beberapa permasalahan kompleksitas terbuka berkaitan dengan pertanyaan apakah keacakan dapat memungkinkan penyelesaian permasalahan dalam waktu yang lebih singkat, seperti pada permasalahan P = BPP.Konvergensi algoritma pencarian lokal stokastik menuju solusi optimal terkadang dapat terjadi sebagai akibat dari kemungkinan perpindahan dari satu solusi ke solusi lainnya dalam ruang pencarian pada setiap iterasi. Namun, sifat semantik penting dari algoritma pencarian lokal stokastik, termasuk kemampuannya untuk menemukan solusi optimal atau solusi dalam jarak tertentu dari nilai optimal, seringkali tidak dapat ditentukan secara umum. Hal ini disebabkan kemampuan algoritma ini untuk mensimulasikan programapa pun, terutama jika bahan dasarnya dimaksudkan sederhana.

Disadur dari : en.wikipedia.org

Trial and error 

Trial and error, metode dasar pemecahan masalah, melibatkan upaya berulang dan bervariasi yang berlanjut hingga kesuksesan tercapai atau praktisi berhenti mencoba. C. Lloyd Morgan menciptakan istilah ini setelah bereksperimen dengan ungkapan serupa seperti “percobaan dan kegagalan” dan “percobaan dan praktik.” Dalam kanon, perilaku hewan dijelaskan secara sederhana dan, dengan asumsi melibatkan proses mental yang lebih tinggi, dapat dijelaskan sebagai pembelajaran melalui coba-coba. Misalnya, Edward Lee Thorndike menggunakan kucing dalam eksperimen laboratorium untuk mendemonstrasikan hukum pengaruh terhadap pembelajaran dan menemukan bahwa hasil positif mendorong pembelajaran.

B. F. Skinner kemudian memperluas konsep ini dengan pengkondisian operan. Trial and error juga digunakan dalam ilmu komputer sebagai metode "build and test" dan dalam matematika, misalnya dalam menyelesaikan persamaan dengan menebak dan memeriksa. Meskipun trial and error adalah salah satu pendekatan dasar pemecahan masalah, ada juga metode perantara seperti empirisme terbimbing, yang memandu proses pemecahan masalah dengan menggunakan teori.Pendekatan yang mencerminkan rasionalisme kritis Karl Popper ini merupakan bagian dari kerangka pemikiran yang dapat digunakan dalam konteks berbeda.

Metodologi

Pendekatan coba-coba (trial-and-error) paling berhasil digunakan pada permasalahan dan permainan sederhana dan sering kali menjadi pilihan terakhir ketika aturan yang jelas tidak dapat diterapkan. Hal ini tidak berarti bahwa pendekatan ini pada dasarnya ceroboh, karena seseorang bisa saja bersifat metodis dalam memanipulasi variabel untuk menyingkirkan kemungkinan-kemungkinan yang dapat membawa kesuksesan. Namun cara ini sering digunakan oleh orang-orang yang memiliki sedikit pengetahuan di bidangsoal. Pendekatan coba-coba diperiksa dari perspektif komputasi alami.

Aplikasi paling sederhana

Ashby (1960) menyajikan tiga strategi sederhana untuk memecahkan masalah pelatihan dasar yang sama dengan efisiensi yang sangat berbeda. Misalnya, jika kita mengatur 1000 tombol hidup/mati dalam kombinasi tertentu dengan percobaan acak, setiap percobaan berlangsung selama satu detik, maka strateginya adalah sebagai berikut:

Metode perfeksionis, di mana segala sesuatu harus berjalan baik atau tidak sama sekali tanpa upaya mempertahankan keberhasilan parsial, diperkirakan akan memakan waktu lebih dari 10^301 detik. Kemudian, rangkaian pengujian sakelar, di mana beberapa berhasil, memiliki durasi rata-rata 500 detik. Terakhir, pengujian paralel namun individual terhadap semua sakelar pada waktu yang sama hanya memerlukan waktu satu detik.

Perlu diketahui bahwa yang mendasari anggapan tersebut adalah anggapan bahwa kecerdasan atau persepsi tidak digunakan untuk menyelesaikan masalah. Namun, kehadiran beberapa strategi memberikan peluang untuk mempertimbangkan domain pemrosesan terpisah atau “tingkat lebih tinggi”, yang dikenal sebagai “tingkat meta,” di atas mekanisme manajemen saklar. Pada tingkat ini, strategi yang berbeda dapat dipilih secara acak, sehingga menciptakan pendekatan coba-coba dengan karakteristik berbeda.

Hirarki

Buku Ashby mengembangkan konsep "meta-level" menjadi urutan level rekursif yang disusun satu di atas yang lain dalam hierarki yang sistematis. Dalam kerangka ini, Ashby berpendapat bahwa kecerdasan manusia muncul dari organisasi seperti itu, yang sangat bergantung pada pendekatan “trial and error” pada setiap tahap baru, namun pada akhir proses tersebut berkembang menjadi apa yang kita sebut “kecerdasan” tahu. Oleh karena itu, tingkat teratas hierarki pada setiap tahap mungkin masih bergantung pada trial and error sederhana.

Traill (1978-2006) mencatat bahwa hierarki yang diusulkan oleh Ashby mungkin tumpang tindih dengan teori tahapan perkembangan Piaget yang terkenal. Menurut Piaget, anak-anak pertama-tama belajar melalui aktivitas yang kurang lebih acak dan kemudian harus belajar dari konsekuensinya, mirip dengan pendekatan “trial and error” acak yang dijelaskan oleh Ashby dalam konteks hierarki tersebut.Hal ini menciptakan kesejajaran antara konsep Ashby dan teori Piaget tentang pembelajaran manusia dan perkembangan kognitif.

Aplikasi

Traill (2008, khususnya Tabel “S” di halaman 31) mengikuti pendekatan Jerne dan Popper dan berasumsi bahwa strategi coba-coba dapat menjadi dasar bagi semua sistem penangkapan pengetahuan, terutama pada tahap awal pengembangannya. . Dalam studinya, Traill mengidentifikasi empat sistem utama yang terlibat dalam penerapan strategi coba-coba: seleksi alam, yang "mendidik" DNA spesies, otak individu (yang baru saja kita bahas), "otak" sosial seperti cabang ilmu pengetahuan masyarakat dan sistem imun adaptif. Konsep ini mendukung pandangan bahwa trial and error tidak hanya sekedar metode pemecahan masalah, tetapi juga dapat menjadi dasar berbagai sistem untuk membangun dan mengembangkan pengetahuan.

Fitur

Trial and error memiliki beberapa karakteristik yang dapat dikenali. Pertama, metode ini berorientasi pada solusi, artinya metode ini tidak berusaha memahami mengapa suatu solusi berhasil melalui trial and error, namun hanya berfokus pada fakta bahwa solusi tersebut dapat ditemukan. Kedua, pendekatan ini bersifat spesifik terhadap permasalahan yang dihadapi dan tidak cenderung menggeneralisasi solusi terhadap permasalahan lainnya. Selain itu, trial and error dianggap suboptimal karena tujuannya biasanya untuk menemukan solusi, bukan keseluruhan spektrum solusi, dan solusi terbaik tidak selalu ditemukan. Terakhir, metode coba-coba dapat dilakukan dengan sedikit atau tanpa pengetahuan tentang subjek yang ada, menjadikannya pendekatan yang layak dan tidak memerlukan pemahaman mendalam.

Metode trial and error dapat digunakan untuk mencari semua solusi atau solusi terbaik dalam situasi dimana terdapat beberapa kemungkinan solusi. Untuk menemukan semua solusi, orang dapat menuliskan setiap solusi yang mereka temukan dan terus mencobanya hingga semua opsi telah dicoba. Untuk mencari solusi terbaik, setelah semua solusi ditemukan, individu dapat membandingkannya berdasarkan kriteria yang telah ditentukan. Adanya kriteria tersebut merupakan prasyarat untuk menemukansolusi terbaik. Ketika hanya ada satu solusi yang mungkin, seperti ketika menyusun sebuah puzzle, solusi yang ditemukan adalah satu-satunya dan dianggap yang terbaik.

Contoh

Secara tradisional, metode utama yang digunakan dalam penemuan obat baru seperti antibiotik adalah trial and error, di mana ahli kimia menguji bahan kimia yang dipilih secara acak untuk menemukan bahan kimia yang mempunyai efek yang diinginkan. Dalam pendekatan yang lebih canggih, mereka memilih sejumlah kecil bahan kimia dan menggunakan hubungan struktur-aktivitas. Metode ini juga digunakan dalam berbagai disiplin ilmu, misalnya pada bidang teknik polimer. Dalam konteks video game, pemain menggunakan trial and error untuk mengatasirintangan atau mengalahkan bos dengan mencoba berbagai strategi. Tim olahraga menggunakan pendekatan ini untuk lolos dan maju ke babak playoff dengan mencoba berbagai taktik dan formasi.

Dalam metode ilmiah, terjadi trial and error dalam merumuskan dan menguji hipotesis. Evolusi biologis dapat dipandang sebagai bentuk coba-coba melalui mutasi acak dan variasi genetik seksual. Contoh lain termasuk algoritma genetika, simulasi anil dan pembelajaran penguatan. Meskipun Bogosort tidak efisien, ini dapat dipandang sebagai metode penyortiran trial-and-error. Laba-laba pelompat dari genus Portia menggunakan trial and error untuk menemukan dan menghafal taktik baru melawan mangsa yang tidak diketahui.Penelitian menunjukkan bahwa bahkan di lingkungan buatan, laba-laba ini dapat menggunakan trial and error untuk mencapai tujuan tertentu.

Disadur dari : https://en.wikipedia.org/wiki/Trial_and_error

Metode Interatif

Dalam matematika komputasi, metode iteratif adalah prosedur matematika yang menggunakan nilai awal untuk menghasilkan rangkaian perkiraan solusi yang meningkat terhadap suatu kelas masalah, dengan perkiraan ke-n diturunkan dari perkiraan sebelumnya. Implementasi khusus dari metode iteratif, termasuk kriteria terminasi, adalah algoritma metode iteratif. Suatu metode iteratif dikatakan konvergen jika barisan-barisan yang bersesuaian konvergen pada pendekatan pertama tertentu. Biasanya, analisis konvergensi yang ketat secara matematis dilakukan secara berulang; Namun, prosedur berulang berdasarkan heuristik juga umum dilakukan.

Metode langsung, sebaliknya, berupaya memecahkan masalah dengan menggunakan serangkaian operasi terbatas.Jika tidak ada kesalahan pembulatan, metode langsung memberikan solusi yang akurat (misalnya menyelesaikan sistem persamaan linear dengan eliminasi Gaussian). Untuk persamaan nonlinier, metode iteratif seringkali merupakan satu-satunya pilihan. Namun, metode iteratif juga sering berguna untuk permasalahan linier dengan banyak variabel (terkadang hingga jutaan), dimana metode langsung akan terlalu mahal (dan dalam beberapa kasus tidak mungkin) bahkan dengan daya komputasi terbaik yang tersedia.

Titik tetap yang menarik

Jika persamaan dapat ditulis sebagai f(x) = x dan penyelesaian x adalah titik tarik-menarik tetap dari f, maka kita dapat memulai dari titik x1 pada daerah tarik-menarik x dan himpunan xn+ 1 = f(xn) untuk n 1, dan barisan {xn} n 1 akan konvergen untuk menyelesaikan x. Di sini xn adalah pendekatan atau iterasi ke-n dari x dan xn+1 adalah iterasi berikutnya atau n+1 x. Alternatifnya, metode numerik sering kali menggunakan eksponen dalam tanda kurung. agar tidak mengalihkan perhatian dari petunjuk yang mempunyai arti lain. (Contoh: x(n+1) = f(x(n)).) Jika fungsi f dapat terdiferensiasi kontinu, syarat yang cukup untuk konvergensi adalah bahwa jari-jari spektral turunan dibatasi secara ketat oleh kesatuan di sekitar titik tetap.Jika kondisi ini terpenuhi pada suatu titik tertentu, maka harus ada lingkungan yang cukup kecil (cekungan daya tarik).

Sistem linier

Untuk sistem persamaan linier, dua kelas utama metode iteratif adalah metode iteratif stasioner dan metode subruang Krylov yang lebih umum.

Metode iteratif stasioner

pengantar

Metode iteratif stasioner menyelesaikan sistem linier dengan operator yang mendekati operator aslinya; dan berdasarkan kesalahan pengukuran pada hasil (sisa), buatlah “persamaan koreksi” yang proses ini diulangi. Meskipun metode ini mudah untuk diturunkan, diterapkan, dan dianalisis, konvergensi hanya dijamin untuk kelas matriks tertentu.

Definisi

Sebuah metode iteratif didefinisikan oleh

dan untuk sistem linier tertentu  dengan solusi eksak kesalahan oleh

Metode iteratif disebut linier jika terdapat matriks sedemikian itu

dan matriks ini disebut matriks iterasi. Metode iteratif dengan matriks iterasi tertentu  disebut konvergen jika berikut ini berlaku

Sebuah teorema penting menyatakan bahwa untuk suatu metode iteratif dan matriks iterasinya konvergen jika dan hanya jika jari-jari spektralnya lebih kecil daripada kesatuan, yaitu

Metode iteratif dasar bekerja dengan membagi matriks menjadi

dan di sini matriks  harus mudah dibalik. Metode iteratif sekarang didefinisikan sebagai

Dari sini berikut bahwa matriks iterasi diberikan oleh

Contoh

Contoh dasar metode iteratif stasioner menggunakan pemisahan matriks seperti

di mana hanyalah bagian diagonal dari , dan adalah bagian segitiga bawah dari . Masing-masing, adalah bagian segitiga atas dari .

Metode Richardson:

Metode Jacobi:

Metode Jacobi teredam:

Metode Gauss–Seidel:

Metode over-relaksasi (SOR):

Relaksasi berlebihan berurutan (SSOR):

Metode iteratif stasioner linier juga disebut metode relaksasi.

Metode subruang Krylov

Metode subruang Krylov terdiri dari pembuatan basis dari barisan pangkat matriks yang berurutan dikalikan dengan sisa awal (urutan Krylov). Perkiraan solusi kemudian dibuat dengan meminimalkan residu di subruang yang dibuat. Metode prototipe kelas ini adalah metode gradien konjugasi (CG), yang mengasumsikan bahwa matriks sistem A terdefinisi positif secara simetris. Untuk nilai simetris (dan mungkin tak terhingga), metode residu minimum(MINRES) dapat digunakan. Untuk matriks non-simetris, metode seperti metode residu terkecil yang digeneralisasi (GMRES) dan metode gradien bikonjugasi (BiCG) telah diturunkan.

Konvergensi metode subruang Krylov

Karena metode ini membentuk basis, terbukti bahwa metode tersebut konvergen dalam N iterasi, di mana N adalah ukuran sistem. Namun, dengan adanya kesalahan pembulatan, pernyataan ini tidak berlaku; apalagi, dalam praktiknya N bisa sangat besar, dan proses iteratif mencapai akurasi yang cukup jauh lebih awal. Analisis metode ini sulit, tergantung pada fungsi spektrum operator yang rumit.

Prakondisi

Operator aproksimasi yang muncul dalam metode iteratif stasioner juga dapat digabungkan dalam metode subruang Krylov seperti GMRES (sebagai alternatif, metode Krylov yang telah diprakondisikan dapat dianggap sebagai percepatan metode iteratif stasioner), di mana mereka menjadi transformasi dari operator asli ke kondisi yang mungkin lebih baik. satu. Konstruksi preconditioners adalah area penelitian yang besar.

Sejarah

Jamshīd al-Kāsh menggunakan metode iteratif untuk menghitung sinus 1° dan dalam Risalah tentang Akord dan Sinus dengan sangat presisi. Salah satu metode berulang pertama untuk menyelesaikan sistem linier muncul dalam surat dari Gauss kepada seorang siswa. Dia mengusulkan penyelesaian sistem persamaan 4 x 4 dengan berulang kali mencari suku dengan sisa terbesar.

Teori metode iteratif stasioner tertanam kuat dalam karya D.M. Muda sejak tahun 1950-an. Metode gradien konjugasi juga ditemukan pada tahun 1950-an, terlepas dari pengembangannya oleh Cornelius Lanczos, Magnus Hestenes dan Eduard Stiefel, namun sifat dan penerapannya masih sedikit dipahami pada saat itu. Baru pada tahun 1970-an diketahui bahwa metode adjoint bekerja sangat baik untuk persamaan diferensial parsial, khususnya persamaan elips.

Disadur dari: en.wikipedia.org

Sistem kompleks

Sistem kompleks terdiri dari banyak komponen yang saling berinteraksi, seperti iklim global Bumi, organisme, atau jaringan listrik. Perilaku sistem kompleks sulit dimodelkan karena adanya ketergantungan, persaingan, dan interaksi antara bagian-bagiannya. Sistem seperti ini cenderung menunjukkan sifat-sifat seperti nonlinier, kemunculan, keteraturan spontan, adaptasi, dan putaran umpan balik. Representasi umum untuk sistem kompleks adalah jaringan, di mana node merepresentasikan komponen dan tautan merepresentasikan interaksi. Studi tentang sistem kompleks adalah pendekatan interdisipliner yang menyelidiki perilaku kolektif dan interaksi sistem dengan lingkungannya. Bidang ini mencakup kontribusi dari berbagai disiplin ilmu seperti fisika, ilmu sosial, matematika, biologi, dan lainnya, dan menawarkan paradigma alternatif terhadap reduksionisme dengan fokus pada pemahaman perilaku sistem sebagai suatu kesatuan.

Konsep kunci

Sistem

Sistem terbuka menyiratkan aliran input dan output dengan lingkungan dan memfasilitasi pertukaran materi, energi, atau informasi. Sistem yang kompleks adalah tentang perilaku dan sifat sistem, dimana suatu sistem membentuk satu kesatuan dengan batas-batas yang ditentukan melalui interaksi dan ketergantungan unit-unitnya. Sifat dan perilaku suatu sistem dapat menimbulkan karakteristik unik dari interaksi dengan lingkungan atau respons bagian-bagian sistem terhadap rangsangan eksternal. Konsep perilakuini menekankan pada studi proses dari waktu ke waktu, dan dalam konteks sistem yang kompleks, teori sistem memberikan kerangka kerja untuk memeriksa bagaimana hubungan dan ketergantungan antar bagian dari suatu sistem membentuk sifat-sifat suatu sistem. dari keseluruhan sistem. Teori sistem juga mendukung pendekatan pemodelan interdisipliner dan menganalisis sifat-sifat umum yang menghubungkan sistem dari berbagai disiplin ilmu.Konsep khusus seperti kemunculan, putaran umpan balik, dan adaptasi dalam sistem yang kompleks berawal dari teori sistem.

Kompleksitas

Agar suatu sistem menunjukkan kompleksitas berarti bahwa perilaku sistem tidak dapat dengan mudah disimpulkan dari sifat-sifatnya. Pendekatan pemodelan apa pun yang mengabaikan kesulitan-kesulitan tersebut atau mencirikannya sebagai kebisingan pasti akan menghasilkan model yang tidak akurat dan tidak berguna. Belum ada teori yang sepenuhnya umum tentang sistem kompleks yang muncul untuk mengatasi masalah ini, sehingga peneliti harus menyelesaikannya dalam konteks khusus domain. Peneliti dalam sistem yang kompleks mengatasi masalah ini dengan melihat tugas utama pemodelan untuk menangkap, bukan mengurangi, kompleksitas sistem masing-masing kepentingan.

Meskipun belum ada definisi kompleksitas yang diterima secara umum, ada banyak contoh pola dasar kompleksitas. Sistem dapat menjadi kompleks jika, misalnya, mereka memiliki perilaku kacau (perilaku yang menunjukkan kepekaan ekstrim terhadap kondisi awal, di antara sifat-sifat lainnya), atau jika mereka memiliki sifat muncul (sifat yang tidak terlihat dari komponennya secara terpisah tetapi dihasilkan dari hubungan dan dependensi yang mereka bentuk ketika ditempatkan bersama dalam suatu sistem), atau jika mereka secara komputasi sulit untuk dimodelkan (jika mereka bergantung pada sejumlah parameter yang tumbuh terlalu cepat sehubungan dengan ukuran sistem).

Jaringan

Komponen yang berinteraksi dari sistem yang kompleks membentuk jaringan, yang merupakan kumpulan objek diskrit dan hubungan di antara mereka, biasanya digambarkan sebagai grafik berarah dari simpul yang dihubungkan oleh tepi. Jaringan dapat menggambarkan hubungan antara individu dalam suatu organisasi, antara gerbang logika dalam suatu sirkuit, antara gen dalam jaringan pengatur gen, atau antara kumpulan entitas terkait lainnya.

Jaringan sering menggambarkan sumber kompleksitas dalam sistem yang kompleks. Mempelajari sistem yang kompleks sebagai jaringan, oleh karena itu, memungkinkan banyak aplikasi yang berguna dari teori graf dan ilmu jaringan. Banyak sistem yang kompleks, misalnya, juga merupakan jaringan yang kompleks, yang memiliki sifat-sifat seperti transisi fase dan distribusi derajat hukum pangkat yang dengan mudah memunculkan perilaku yang muncul atau kacau. Fakta bahwa jumlah tepi dalam graf lengkap tumbuh secara kuadratik dalam jumlah simpul memberi penjelasan tambahan pada sumber kompleksitas dalam jaringan besar: ketika jaringan tumbuh, jumlah hubungan antar entitas dengan cepat mengerdilkan jumlah entitas dalam jaringan.

Nonlinearity

 

Solusi sampel dalam atraktor Lorenz ketika ρ = 28, σ = 10, dan β = 8/3

Emergence

Glider Gun milik Gosper menciptakan "glider" dalam robot seluler Conway's Game of Life[2]

Fitur umum lainnya dari sistem yang kompleks adalah adanya perilaku dan properti yang muncul: ini adalah ciri-ciri sistem yang tidak terlihat dari komponen-komponennya dalam isolasi tetapi dihasilkan dari interaksi, ketergantungan, atau hubungan yang mereka bentuk ketika ditempatkan bersama dalam suatu sistem. Kemunculan secara luas menggambarkan penampilan perilaku dan sifat tersebut, dan memiliki penerapan pada sistem yang dipelajari baik dalam ilmu sosial maupun fisika. Sementara kemunculan sering digunakan untuk merujuk hanya pada kemunculan perilaku terorganisir yang tidak direncanakan dalam sistem yang kompleks, kemunculan juga dapat merujuk pada kehancuran suatu organisasi; itu menggambarkan setiap fenomena yang sulit atau bahkan tidak mungkin diprediksi dari entitas yang lebih kecil yang membentuk sistem.

Salah satu contoh sistem kompleks yang sifat kemunculannya telah dipelajari secara ekstensif adalah otomata seluler. Dalam otomat seluler, kisi-kisi sel, masing-masing memiliki salah satu dari banyak keadaan terhingga, berkembang menurut seperangkat aturan sederhana. Aturan ini memandu "interaksi" setiap sel dengan tetangganya. Meskipun aturan hanya didefinisikan secara lokal, aturan tersebut telah terbukti mampu menghasilkan perilaku yang menarik secara global, misalnya dalam Game of Life karya Conway.

Spontaneous order and self-organization (Tatanan spontan dan pengaturan diri)

Ketika kemunculan menggambarkan munculnya tatanan yang tidak direncanakan, itu adalah tatanan spontan (dalam ilmu sosial) atau swaorganisasi (dalam ilmu fisika). Urutan spontan dapat dilihat dalam perilaku kawanan, di mana sekelompok individu mengoordinasikan tindakan mereka tanpa perencanaan terpusat. Self-organization dapat dilihat dalam simetri global kristal tertentu, misalnya simetri radial kepingan salju yang tampak, yang muncul dari gaya tarik dan tolak lokal murni antara molekul air dan lingkungan sekitarnya.

Adaptasi

Sistem adaptif kompleks adalah kasus khusus dari sistem kompleks yang adaptif karena memiliki kapasitas untuk berubah dan belajar dari pengalaman. Contoh sistem adaptif yang kompleks termasuk pasar saham, serangga sosial dan koloni semut, biosfer dan ekosistem, otak dan sistem kekebalan, sel dan embrio yang sedang berkembang, kota, bisnis manufaktur, dan usaha berbasis kelompok sosial manusia apa pun di sistem budaya dan sosial seperti partai politik atau komunitas.

Fitur
Sistem yang kompleks mungkin memiliki ciri-ciri berikut:

Sistem yang kompleks mungkin terbuka

Sistem yang kompleks biasanya merupakan sistem terbuka — yaitu, mereka ada dalam gradien termodinamika dan energi yang terdisipasi. Dengan kata lain, sistem kompleks seringkali jauh dari kesetimbangan energetik: tetapi meskipun fluks ini, mungkin ada stabilitas pola lihat sinergi.

Sistem yang kompleks dapat menunjukkan transisi kritis

Transisi kritis adalah perubahan mendadak pada keadaan suatu sistem, seperti ekosistem, iklim, atau sistem kompleks lainnya, yang terjadi ketika perubahan kondisi melewati titik belok atau bifurkasi. Dalam representasi grafis, arah kritis penundaan menunjukkan keadaan sistem di masa depan setelah transisi, dengan kemungkinan penundaan umpan balik negatif yang dapat menyebabkan osilasi atau dinamika kompleks yang lemah.

Sistem yang kompleks mungkin bersarang

Komponen-komponen suatu sistem yang kompleks juga dapat berupa sistem yang kompleks itu sendiri. Misalnya, perekonomian terdiri dari organisasi-organisasi, yang terdiri dari individu-individu, dan individu-individu ini terdiri dari sel-sel, yang semuanya merupakan sistem yang kompleks. Interaksi dalam jaringan bipartit yang kompleks dapat dilakukan secara bertingkat, khususnya dalam jaringan ekologi dan organisasi bipartit. Struktur tersarang dalam jaringan ditemukan mendukung fasilitasi tidak langsung, meningkatkan ketahanan sistemdalam kondisi yang menantang dan meningkatkan potensi perubahan rezim yang sistemik.

Jaringan multiplisitas yang dinamis

Selain aturan penggandengan, struktur jaringan dinamis dari sistem yang kompleks juga sangat penting. Dalam konteks ini, jaringan dunia kecil atau jaringan tanpa skala biasanya digunakan, yang dicirikan oleh banyak interaksi lokal dan sejumlah kecil koneksi antar wilayah. Sistem alami yang kompleks biasanya memiliki topologi seperti itu. Misalnya, di korteks manusia terdapat konektivitas lokal yang padat dan beberapa proyeksi aksonal yang sangat panjang antara wilayah di dalam korteks dan wilayah otak lainnya.

Dapat menghasilkan fenomena yang muncul

Sistem yang kompleks dapat menunjukkan perilaku yang muncul, yang berarti bahwa hasilnya dapat ditentukan oleh aktivitas komponen dasar sistem, namun sifat tersebut hanya dapat dipahami pada tingkat yang lebih tinggi. Misalnya, jaring makanan empiris menunjukkan ciri-ciri invarian skala reguler di ekosistem akuatik dan darat ketika dianalisis pada tingkat spesies trofik gabungan. Contoh lainnya adalah perilaku rayap di dalam gundukan tanah, yang perkembangan fisiologis, biokimia, dan biologisnya terjadi pada satu tingkat analisis, sedangkan perilaku sosial dan struktur gundukan mereka merupakan ciri-ciri komunitas rayap yang muncul dan perlu dianalisis pada tingkatan lain.

Hubungan tidak linier

Dalam istilah praktis, ini berarti gangguan kecil dapat menyebabkan efek yang besar (lihat efek kupu-kupu), efek proporsional, atau bahkan tanpa efek sama sekali. Dalam sistem linier, akibat selalu berbanding lurus dengan sebab. Lihat nonlinier.

Hubungan mengandung putaran umpan balik

Umpan balik negatif (redaman) dan positif (memperkuat) selalu ditemukan dalam sistem yang kompleks. Efek dari perilaku elemen diberi umpan balik sedemikian rupa sehingga elemen itu sendiri diubah.

Sejarah

Studi tentang sistem yang kompleks masih relatif baru dibandingkan dengan disiplin ilmu yang sudah mapan seperti fisika dan kimia, meskipun manusia telah mempelajari sistem tersebut selama ribuan tahun. Sejarah perkembangan ilmu sistem yang kompleks mencakup kontribusi matematika pada identifikasi kekacauan dalam sistem deterministik dan studi jaringan saraf. Gagasan pengorganisasian mandiri terkait dengan termodinamika nonequilibrium yang diperkenalkan oleh Ilya Prigogine dan terkait dengan karya Hartree-Fock dalam kimia kuantum. Perkembangan mazhab ekonomi Austria, yang menyatakan bahwa tatanan pasar muncul secara spontan, memperkenalkan unsur-unsur kompleksitas ke dalam pemikiran ekonomi. Pada abad ke-20, Friedrich Hayek memperkenalkan pemikiran kompleks ke berbagai disiplin ilmu, termasuk ekonomi, psikologi, biologi, dan sibernetika.Pada tahun 1984, Institut Santa Fe didirikan, lembaga penelitian pertama yang berfokus secara khusus pada sistem yang kompleks. Sejak akhir tahun 1990-an, fisikawan matematika semakin tertarik mempelajari fenomena ekonomi dan menciptakan paradigma baru dalam ilmu ekonomi yang dikenal sebagai “fisika ekonomi”. Hadiah Nobel Fisika tahun 2021 dianugerahkan kepada Syukuro Manabe, Klaus Hasselmann, dan Giorgio Parisi atas karya mereka dalam memahami sistem yang kompleks, khususnya dalam menciptakanmodel komputer mengenai dampak pemanasan global yang lebih akurat.

Aplikasi

Kompleksitas dalam praktik

Pendekatan tradisional untuk menghadapi kompleksitas adalah dengan mengurangi atau membatasinya. Biasanya, ini melibatkan kompartementalisasi: membagi sistem besar menjadi bagian-bagian yang terpisah. Organisasi, misalnya, membagi pekerjaan mereka menjadi departemen yang masing-masing menangani masalah yang berbeda. Sistem rekayasa sering dirancang menggunakan komponen modular. Namun, desain modular menjadi rentan terhadap kegagalan ketika muncul masalah yang menjembatani divisi tersebut.

Manajemen kompleksitas

Ketika proyek dan akuisisi menjadi semakin kompleks, perusahaan dan pemerintah menghadapi tantangan untuk mengelola mega-akuisisi secara efektif seperti Sistem Pertempuran Masa Depan Angkatan Darat. Akuisisi seperti FCS mengandalkan jaringan bagian-bagian yang saling berhubungan dan berinteraksi dengan cara yang tidak terduga. Seiring dengan meningkatnya sifat jaringan dan kompleksitas pengadaan, perusahaan harus menemukan cara untuk mengelola kompleksitas ini, sementara pemerintah dihadapkan pada tugas menyediakan tata kelolayang efektif untuk memastikan fleksibilitas dan ketahanan.

Ekonomi kompleksitas

Dalam bidang ekonomi kompleks yang sedang berkembang, alat prediksi baru telah dikembangkan untuk menjelaskan pertumbuhan ekonomi. Untuk membuat perkiraan PDB tahun 2020, digunakan model seperti yang dibuat oleh Santa Fe Institute pada tahun 1989 dan Indeks Kompleksitas Ekonomi (ECI) terbaru yang diperkenalkan oleh fisikawan MIT César A. Hidalgo dan ekonom Harvard Ricardo Hausmann. Kuantifikasi pengulangan digunakan untuk menangkap karakteristik siklus bisnisdan pembangunan ekonomi. Indeks Korelasi Kuantifikasi Perulangan (RQCI) dikembangkan untuk menguji korelasi dalam sinyal sampel dan kemudian menerapkannya pada deret waktu komersial.Indeks telah terbukti mendeteksi perubahan tersembunyi dalam rangkaian waktu dan membantu memprediksi transisi dari fase biasa ke fase kacau. Analisis kuantifikasi berulang juga dapat membedakan variabel makroekonomi dan menyoroti ciri-ciri tersembunyi dari dinamika ekonomi.

Kompleksitas dan pendidikan

Forsman, Moll, dan Linder fokus pada pertanyaan tentang ketekunan siswa dalam studi mereka dan menguji "kemampuan untuk menggunakan ilmu kompleksitas sebagai kerangka untuk memperluas penerapan metodologi pada penelitian olahraga." Mereka menemukan bahwa “menyematkan analisis jaringan sosial dalam perspektif ilmiah yang kompleks menawarkan penerapan baru yang kuat untuk berbagai topik penelitian pendidikan jasmani (PER).”

Kompleksitas dan biologi

Ilmu kompleksitas telah diterapkan pada organisme hidup, khususnya sistem biologis. Bidang penelitian berkaitan dengan penciptaan dan pengembangan sistem cerdas. Analisis parameter sistem intelektual, pola pembentukan dan perkembangannya, serta struktur dan fungsinya memungkinkan kita mengukur dan membandingkan kapasitas komunikasi, jumlah komponen sistem intelektual, dan jumlah koneksi sukses yang bertanggung jawab atas kerjasama tersebut. Dalam fisiologi fraktal, sinyal tubuh seperti detak jantung atau aktivitas otak dikarakterisasi menggunakan indeks entropi atau fraktal untuk menilai kondisi dan kesehatan sistem yang mendasarinya serta untuk mendiagnosis potensi gangguan dan penyakit.

Kompleksitas dan pemodelan

Friedrich Hayek memberikan kontribusi penting terhadap teori sistem kompleks dengan membedakan kemampuan manusia untuk memprediksi perilaku sistem sederhana dan sistem kompleks menggunakan model. Hayek percaya bahwa ilmu ekonomi dan ilmu tentang fenomena kompleks secara umum tidak dapat dimodelkan sebagai ilmu yang menangani fenomena sederhana, seperti fisika. Menurutnya, pemodelan fenomena yang kompleks hanya dapat memungkinkan prediksi terhadap pola, namun tidak dapat memprediksi secara tepat seperti fenomena yang tidak kompleks.

Kompleksitas dan teori kekacauan

Teori sistem kompleks berakar pada teori chaos, yang muncul lebih dari satu abad yang lalu dalam karya ahli matematika Perancis Henri Poincaré. Kekacauan dipandang sebagai informasi yang sangat kompleks, bukan kurangnya keteraturan. Sistem chaos tetap bersifat deterministik, namun perilaku jangka panjangnya sulit diprediksi secara akurat. Dengan pengetahuan yang sempurna tentang kondisi awal dan persamaan yang relevan, para ahli teori dapat membuat prediksi yang sangat akurat, meskipun dalam praktiknya hal ini sulit. Ilya Prigogine berpendapat bahwa kompleksitas bersifat non-deterministik dan tidak memberikan cara untuk memprediksi masa depan secara akurat.Munculnya teori sistem kompleks menunjukkan adanya wilayah antara keteraturan deterministik dan keacakan kompleks yang dikenal sebagai “batas kekacauan”.

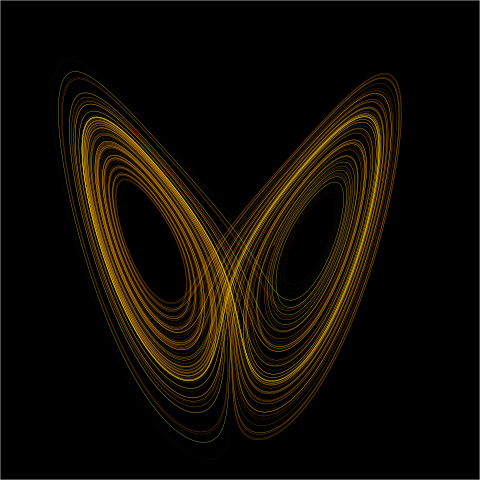
Plot penarik Lorenz.

Saat menganalisis sistem yang kompleks, kepekaan terhadap kondisi awal tidak sepenting teori chaos. Studi tentang kompleksitas adalah kebalikan dari studi tentang kekacauan. Kompleksitas mengacu pada sejumlah besar hubungan dinamis dan sangat kompleks yang menghasilkan pola perilaku sederhana. Dalam ilmu ekonomi dan bisnis, misalnya, penelitian menyoroti dinamika pasar Android, sinkronisasi timbal balik dalam perusahaan, dan regularisasi kekacauan dalam kelompok sel yang meledak secara kacau pada tahun. Perbedaan utama antara sistem chaos dan sistem kompleks terletak pada sejarahnya.Sistem yang kacau tidak bergantung pada sejarah, yang menempatkan sistem dalam tatanan yang kacau. Sebaliknya, sistem yang kompleks berkembang di ambang kekacauan, dipengaruhi oleh sejarah peristiwa yang tidak dapat diubah. Sistem yang kompleks berpotensi menghasilkan perubahan kualitatif yang radikal dengan tetap menjaga integritas sistem, yang dalam konteks sejarah terbatas dapat dianggap sebagai bagian dari sistem yang kacau balau.

 

Complexity and network science (Kompleksitas dan ilmu jaringan)

Sistem yang kompleks umumnya terdiri dari banyak komponen dan interaksinya dapat diwakili oleh suatu jaringan, dimana setiap node mewakili suatu komponen dan link mewakili interaksinya. Misalnya, Internet dapat digambarkan sebagai jaringan di mana komputer berfungsi sebagai node dan koneksi langsung antar komputer berfungsi sebagai koneksi. Jaringan yang kompleks juga dapat ditemukan dalam berbagai konteks, seperti jaringan sosial, ketergantungan pada lembaga keuangan, maskapai penerbangan, dan jaringan biologis.

Disadur dari: en.wikipedia.org

Feedback (Umpan Balik)

Feedback (Umpan balik) terjadi ketika keluaran suatu sistem kembali menjadi masukan, sehingga membentuk rantai sebab-akibat yang membentuk suatu putaran atau rangkaian. Dalam sistem umpan balik, gagasan kausalitas harus ditangani dengan hati-hati karena interaksi antara sistem pertama dan kedua saling mempengaruhi dan menciptakan argumen melingkar yang membuat penalaran berdasarkan sebab dan akibat menjadi sulit. Hal ini memerlukan analisis menyeluruh terhadap keseluruhan sistem. Karl Johan Åström dan Richard M. Murray menjelaskan bahwa umpan balik dalam bisnis adalah transmisi informasi evaluatif atau korektif tentang tindakan, peristiwa, atau proses ke sumber asli atau sumber pengendali.

Sejarah

Umpan balik memiliki sejarah yang panjang, dimulai dengan mekanisme pengaturan mandiri yang sudah ada sejak zaman kuno. Ide umpan balik pertama kali muncul dalam teori ekonomi Inggris pada abad ke-18, namun tidak diakui sebagai abstraksi universal pada saat itu. Katup pelampung, ditemukan pada tahun 270 SM. Di Mesir, ini adalah perangkat umpan balik buatan pertama yang diketahui. Prinsip umpan balik tercermin dalam mekanisme ini, di mana ketinggian air yang rendah membuka katup, menciptakan putaran umpan balikyang menjaga ketinggian air tetap konstan. Pengatur sentrifugal, yang digunakan sejak abad ke-17 untuk mengendalikan kincir angin, menjadi semakin canggih dengan desain James Watt pada tahun 1788, menghasilkan pengendalian kecepatan yang lebih tepat pada mesin uap.Pada tahun 1868, James Clerk Maxwell berkontribusi pada teori klasik kontrol umpan balik dengan artikel “On Governors.” Istilah “umpan balik” pertama kali digunakan oleh Karl Ferdinand Braun pada tahun 1909 dan merujuk pada kopling yang tidak diinginkan dalam sirkuit elektronik.

Pada tahun 1912, penggunaan umpan balik yang disengaja pada amplifier elektronik menghasilkan peningkatan penguatan, dan istilah ini menjadi umum pada tahun 1920. Sejak tahun 1940-an, sibernetika berfokus pada studi tentang mekanisme umpan balik kausal melingkar. Selama bertahun-tahun telah terjadi perdebatan mengenai definisi umpan balik, dengan Ashby (1956) menganjurkan definisi "sirkularitas tindakan", sementara Ramaprasad (1983) lebih menekankan penggunaannya dalam teori manajemen, mendefinisikannya sebagai informasi tentang kesenjangan dalam organisasi. umpan balik untuk mengubah sistem. Menutup kesenjangan melalui tindakan yang tepat.

Jenis

Feedback Positif dan Negatif

Umpan balik positif terjadi bila sinyal keluaran sefasa dengan sinyal masukan, sedangkan umpan balik negatif terjadi bila sinyal keluaran sefasa 180° dengan sinyal masukan. Sebagai contoh umpan balik negatif, perhatikan sistem kendali jelajah pada mobil dengan target kecepatan, seperti batas kecepatan. Kecepatan mobil diukur dengan speedometer dan umpan balik negatif digunakan untuk memperbaiki kesalahan kecepatan dengan mengatur throttle dan mengontrol aliran bahan bakar ke mesin.

Istilah “positif” dan “negatif” sehubungan dengan umpan balik sudah digunakan sebelum Perang Dunia Kedua. Gagasan umpan balik positif dimulai pada tahun 1920-an dan dikaitkan dengan sirkuit regeneratif.Pada tahun 1934, Harold Stephen Black merinci penggunaan umpan balik negatif dalam amplifier elektronik, dengan umpan balik positif meningkatkan penguatan sementara umpan balik negatif menurunkannya. Namun, kebingungan segera muncul karena perbedaan penafsiran istilah tersebut oleh para peneliti seperti Friis dan Jensen, yang membedakan umpan balik berdasarkan pengaruhnya terhadap penguatan, bukan tanda dari umpan balik itu sendiri. James Clerk Maxwell sebelumnya telah menjelaskan konsep umpan balikmelalui pergerakan komponen yang terkait dengan pengatur sentrifugal pada mesin uap, membedakan faktor penyebab peningkatan kebisingan atau amplitudo dengan faktor penyebab penurunan kualitas yang sama.

Terminologi

Istilah umpan balik positif dan negatif memiliki definisi berbeda tergantung pada disiplin ilmu yang digunakan. Definisi pertama mengacu pada perubahan jarak antara nilai acuan dengan nilai sebenarnya suatu parameter atau karakteristik, dimana jarak yang bertambah dianggap positif dan jarak yang berkurang dianggap negatif. Definisi kedua mengacu pada valensi tindakan atau efek umpan balik, dimana tindakan yang membuat penerimanya senang dipandang positif, sedangkan tindakan yang membuat penerimanya tidak bahagia dipandang negatif.

Namun, timbul kebingungan karena istilah ini dapat memiliki arti berbeda tergantung konteksnya. Beberapa penulis menggunakan istilah alternatif seperti penguatan diri dan koreksi diri, penguatan dan keseimbangan, peningkatan dan pengurangan kesenjangan, atau regeneratif dan degeneratif. Lebih jauh lagi, dalam definisi kedua, beberapa penulis menganjurkan penggunaan penguatan atau hukuman positif dan negatif daripada umpan balik.

Kebingungan ini mungkin disebabkan oleh sifat umpan balik yang kompleks, yang dapat digunakan untuk memberi informasi atau memotivasi dan mencakup komponen kualitatif dan kuantitatif. Banyak kebingungan juga muncul dari kenyataan bahwa bahkan dalam disiplin ilmu yang sama, istilah “umpan balik positif” atau “umpan balik negatif” dapat digunakan secara berbeda tergantung pada bagaimana nilai diukur atau dirujuk.Kebingungan ini mungkin disebabkan oleh sifat umpan balik yang kompleks, yang dapat digunakan untuk memberi informasi atau memotivasi dan mencakup komponen kualitatif dan kuantitatif. Banyak kebingungan juga muncul dari kenyataan bahwa bahkan dalam disiplin ilmu yang sama, istilah “umpan balik positif” atau “umpan balik negatif” dapat digunakan secara berbeda tergantung pada bagaimana nilai diukur atau dirujuk.

Aplikasi

Matematika dan Sistem Dinamik

Dengan menggunakan properti umpan balik, perilaku sistem dapat diubah untuk memenuhi kebutuhan aplikasi. Sistem dapat dijaga agar tetap stabil, responsif, atau konstan. Hal ini menunjukkan bahwa sistem dinamis dengan umpan balik di tepi kekacauan akan mengalami adaptasi.

Fisika

Sistem fisik memberikan umpan balik melalui interaksi timbal balik dari bagian-bagiannya. Umpan balik juga relevan untuk pengaturan kondisi eksperimental, pengurangan kebisingan, dan kontrol sinyal. Termodinamika sistem yang dikendalikan umpan balik telah menarik perhatian para fisikawan sejak zaman Maxwell, dengan kemajuan terkini mengenai konsekuensi pengurangan entropi dan peningkatan daya.

Biologi

Dalam sistem biologis seperti organisme, ekosistem, atau biosfer, banyak parameter yang harus dikontrol dalam rentang sempit di sekitar nilai optimal dalam kondisi lingkungan tertentu. Perubahan nilai parameter dapat disebabkan oleh perubahan lingkungan internal dan eksternal, dan beberapa kondisi lingkungan memerlukan penyesuaian rentang agar sistem dapat berfungsi. Sistem biologis menggunakan loop kontrol positif dan negatif untuk mempertahankan nilai parameter optimal. Contoh seperti osilasi insulinmenggambarkan salah satu mekanisme ini.

Integritas jaringan dalam sistem biologis dipertahankan melalui interaksi umpan balik antara tipe sel yang berbeda dengan mediator seperti molekul adhesi.Pada kanker, kegagalan mekanisme umpan balik utama dapat mengubah fungsi jaringan. Umpan balik juga memainkan peran penting dalam respon imun dan pemulihan dari infeksi dan cedera. Mekanisme umpan balik pertama kali dijelaskan pada bakteri, dan pada operon genetik, umpan balik bisa positif atau negatif.

Umpan balik dalam skala yang lebih besar dapat mempunyai efek menstabilkan populasi hewan, namun juga dapat mengarah pada siklus predator-mangsa. Dalam zimologi, umpan balik berfungsi sebagai pengaturan aktivitas enzimatik oleh produk hilir atau metabolit dalam jalur metabolisme.Sumbu hipotalamus-hipofisis-adrenal dikendalikan oleh umpan balik positif dan negatif.

Dalam psikologi, umpan balik positif terjadi ketika suatu stimulus memicu pelepasan suatu hormon, yang kemudian memicu pelepasan hormon lain, sehingga membentuk putaran umpan balik positif. Misalnya, orang yang mudah tersipu malu mengalami “siklus rasa malu” di mana kesadaran akan rasa malu memicu rasa malu lebih lanjut, sehingga membentuk siklus yang terus berlanjut.

Sumber: id.wikipedia.org

Matematika komputasi

Matematika komputasi memainkan peran penting dalam hubungan antara matematika dan ilmu komputer, terutama dalam pengembangan algoritma, metode numerik, dan perhitungan simbolik. Di bidang matematika komputasi terapan, fokusnya adalah pada penggunaan konsep matematika untuk meningkatkan dan mengoptimalkan penggunaan komputer dalam konteks matematika terapan. Ini melibatkan penerapan matematika untuk memecahkan masalah dunia nyata dan merancang algoritma yang efisien.

Selain itu, komputasi matematis juga mencakup penggunaan komputer dalam studi masalah matematika berbasis komputer, pencarian metode komputasi matematis yang efisien seperti aljabar komputer, dan teori kompleksitas, yang memperhitungkan perhitungan yang dapat dilakukan dengan menggunakan teknologi yang tersedia. Selain itu, matematika komputasi juga tentang melihat bukti-bukti pendukung, yaitu pembuktian matematis yang dapat dilakukan dengan komputer.Secara umum, matematika komputasi adalah pendekatan holistik yang menggabungkan matematika dan ilmu komputer untuk memecahkan berbagai tantangan matematika dan komputasi dunia nyata.

Bidang-bidang matematika komputasi

Matematika komputasi menjadi bagian tersendiri dari matematika terapan pada awal 1950-an. Sekarang, matematika komputasi memiliki arti atau meliputi:

• Ilmu komputasi, dikenal juga sebagai komputasi ilmiah atau teknik komputasi
• Bagian matematika dari komputasi ilmiah, khususnya analisis numerik, teori metode numerik
• Kompleksitas komputasi
• Aljabar komputer dan sistem aljabar komputer
• Linguistik komputasi, yaitu penggunaan teknik mathematika dan komputer dalam bahasa alami
• Geometri aljabar komputasi
• Teori grup komputasi
• Geometri komputasi
• Teori bilangan komputasi
• Topologi komputasi
• Statistika komputasi
• Teori informasi algoritmik
• Teori permainan algoritmik
• Mathematika ekonomi, yaitu penggunaan matematika dalam ekonomi, finansial dan akuntansi.

Contoh Penerapan Matematika Komputasi

Salah satu contoh penerapan matematika komputasi adalah dalam bidang ilmu komputer, khususnya dalam pengembangan algoritma dan pemodelan permasalahan kompleks. Sebagai contoh, dalam dunia kecerdasan buatan, matematika komputasi digunakan untuk merancang algoritma pembelajaran mesin yang dapat memproses dan menganalisis data besar untuk menghasilkan model yang dapat melakukan prediksi atau pengenalan pola.

Dalam simulasi kejadian fisika atau dinamika sistem kompleks, matematika komputasi juga sangat penting. Misalnya, dalam simulasi cuaca atau iklim, persamaan diferensial parsial dan metode numerik digunakan untuk menggambarkan perubahan kondisi atmosfer dan memprediksi pola cuaca di masa depan.Selain itu, dalam bidang keuangan, matematika komputasi dapat digunakan untuk mengembangkan model matematika yang kompleks untuk memahami perilaku pasar keuangan, mengevaluasi risiko investasi, dan merancang strategi keuangan yang optimal.

Dalam dunia kriptografi, matematika komputasi memainkan peran kunci dalam merancang algoritma enkripsi yang aman, pengujian primalitas, dan pengembangan teknologi keamanan informasi lainnya.Penerapan matematika komputasi juga dapat ditemukan dalam pengembangan perangkat lunak dan pemrosesan data besar, di mana teknik-teknik matematika seperti analisis numerik, aljabar linier numerik, dan metode optimisasi digunakan untuk meningkatkan kinerja algoritma dan sistem komputasi.

Disadur dari: en.wikipedia.org