diklatkerja | Mendaki Bukit

Sebuah permukaan dengan hanya satu maksimum. Teknik mendaki bukit sangat cocok untuk mengoptimalkan permukaan seperti itu, dan akan menyatu dengan maksimum global. (Wikipedia)

Dalam analisis numerik, mendaki bukit adalah teknik optimasi matematis yang termasuk dalam keluarga pencarian lokal. Ini adalah algoritma iteratif yang dimulai dengan solusi arbitrer untuk suatu masalah, kemudian mencoba menemukan solusi yang lebih baik dengan membuat perubahan bertahap pada solusi. Jika perubahan menghasilkan solusi yang lebih baik, perubahan tambahan lainnya dilakukan pada solusi baru, dan seterusnya sampai tidak ada perbaikan lebih lanjut yang dapat ditemukan.

Misalnya, mendaki bukit dapat diterapkan pada masalah salesman keliling. Sangat mudah untuk menemukan solusi awal yang mengunjungi semua kota tetapi kemungkinan akan sangat buruk dibandingkan dengan solusi optimal. Algoritme dimulai dengan solusi semacam itu dan membuat perbaikan kecil untuknya, seperti mengubah urutan kunjungan dua kota. Akhirnya, rute yang jauh lebih pendek kemungkinan akan diperoleh.

Pendakian bukit menemukan solusi optimal untuk masalah cembung – untuk masalah lain hanya akan menemukan optima lokal (solusi yang tidak dapat diperbaiki oleh konfigurasi tetangga), yang belum tentu solusi terbaik (optimal global) dari semua solusi yang mungkin ( ruang pencarian). Contoh algoritma yang memecahkan masalah cembung dengan mendaki bukit termasuk algoritma simpleks untuk pemrograman linier dan pencarian biner.: 253 Untuk mencoba menghindari terjebak dalam optima lokal, seseorang dapat menggunakan restart (yaitu pencarian lokal berulang), atau lebih skema kompleks berdasarkan iterasi (seperti pencarian lokal berulang), atau pada memori (seperti optimasi pencarian reaktif dan pencarian tabu), atau pada modifikasi stokastik tanpa memori (seperti simulasi anil).

Kesederhanaan relatif dari algoritme menjadikannya pilihan pertama yang populer di antara algoritme pengoptimalan. Ini digunakan secara luas dalam kecerdasan buatan, untuk mencapai keadaan tujuan dari simpul awal. Pilihan yang berbeda untuk node berikutnya dan node awal digunakan dalam algoritma terkait. Meskipun algoritme yang lebih canggih seperti simulasi anil atau pencarian tabu dapat memberikan hasil yang lebih baik, dalam beberapa situasi mendaki bukit juga berfungsi dengan baik. Pendakian bukit seringkali dapat menghasilkan hasil yang lebih baik daripada algoritma lain ketika jumlah waktu yang tersedia untuk melakukan pencarian terbatas, seperti dengan sistem waktu nyata, selama sejumlah kecil peningkatan biasanya menyatu pada solusi yang baik (solusi optimal atau pendekatan dekat). Di sisi lain, bubble sort dapat dilihat sebagai algoritme pendakian bukit (setiap pertukaran elemen yang berdekatan mengurangi jumlah pasangan elemen yang tidak teratur), namun pendekatan ini jauh dari efisien bahkan untuk N yang sederhana, karena jumlah pertukaran yang diperlukan bertambah secara kuadrat.

Mendaki bukit adalah algoritme kapan saja: ia dapat mengembalikan solusi yang valid bahkan jika terputus kapan saja sebelum berakhir.

Deskripsi matematika

Mendaki bukit mencoba untuk memaksimalkan (atau meminimalkan) fungsi target $f(\mathbf {x} )$ , di mana $\mathbf {x}$ adalah vektor nilai kontinu dan/atau diskrit. Pada setiap iterasi, mendaki bukit akan menyesuaikan satu elemen di $\mathbf {x}$ dan menentukan apakah perubahan meningkatkan nilai $f(\mathbf {x} )$ . (Perhatikan bahwa ini berbeda dari metode penurunan gradien, yang menyesuaikan semua nilai dalam $\mathbf {x}$ pada setiap iterasi sesuai dengan gradien bukit.) Dengan mendaki bukit, perubahan apa pun yang meningkatkan $f(\mathbf {x} )$ diterima, dan proses berlanjut sampai tidak ada perubahan yang dapat ditemukan untuk meningkatkan nilai $f(\mathbf {x} )$ . Maka $\mathbf {x}$ dikatakan "optimal secara lokal".

Dalam ruang vektor diskrit, setiap nilai yang mungkin untuk $\mathbf {x}$ dapat divisualisasikan sebagai simpul dalam graf. Pendakian bukit akan mengikuti grafik dari titik ke titik, selalu meningkat (atau menurun) secara lokal nilai $f(\mathbf {x} )$ , hingga maksimum lokal (atau minimum lokal ) $x_{m}$ tercapai.

Varian

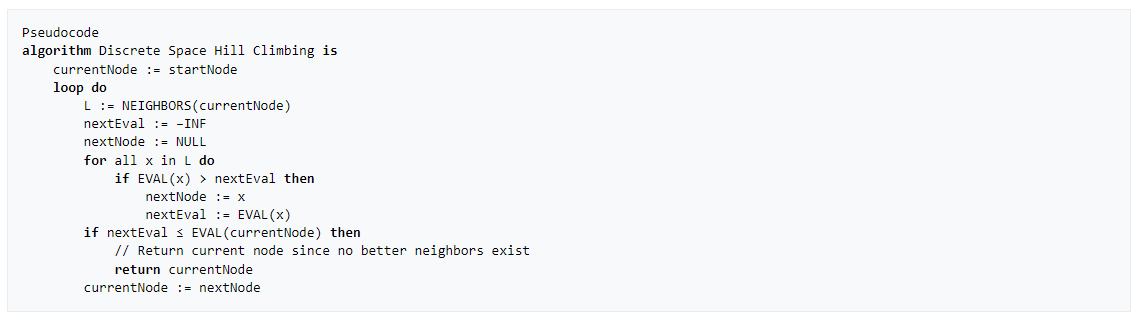
Dalam pendakian bukit sederhana, simpul terdekat pertama dipilih, sedangkan pada pendakian bukit tercuram semua penerus dibandingkan dan yang paling dekat dengan solusi dipilih. Kedua bentuk gagal jika tidak ada node yang lebih dekat, yang mungkin terjadi jika ada maxima lokal di ruang pencarian yang bukan solusi. Pendakian bukit pendakian terjal mirip dengan pencarian terbaik-pertama, yang mencoba semua kemungkinan ekstensi jalur saat ini, bukan hanya satu.

Pendakian bukit stokastik tidak memeriksa semua tetangga sebelum memutuskan bagaimana cara bergerak. Sebaliknya, ia memilih tetangga secara acak, dan memutuskan (berdasarkan jumlah peningkatan pada tetangga itu) apakah akan pindah ke tetangga itu atau memeriksa yang lain.

Penurunan koordinat melakukan pencarian garis sepanjang satu arah koordinat pada titik saat ini di setiap iterasi. Beberapa versi penurunan koordinat secara acak memilih arah koordinat yang berbeda masing-masing erasi.

Pendakian bukit yang dimulai ulang secara acak adalah meta-algoritma yang dibangun di atas algoritma pendakian bukit. Ini juga dikenal sebagai pendakian bukit Shotgun. Ini secara iteratif melakukan pendakian bukit, setiap kali dengan kondisi awal acak $x_{0}$ . $x_{m}$ terbaik dipertahankan: jika rangkaian baru mendaki bukit menghasilkan $x_{m}$ yang lebih baik daripada status tersimpan, ini akan menggantikan status tersimpan.

Pendakian bukit yang dimulai ulang secara acak adalah algoritma yang sangat efektif dalam banyak kasus. Ternyata seringkali lebih baik menghabiskan waktu CPU menjelajahi ruang, daripada mengoptimalkan dengan hati-hati dari kondisi awal

Masalah

Maksimum lokal

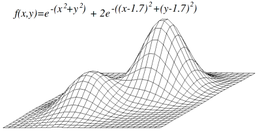
Sebuah permukaan dengan dua maxima lokal. (Hanya salah satunya adalah maksimum global.) Jika seorang pendaki bukit dimulai di lokasi yang buruk, mungkin menyatu ke maksimum yang lebih rendah.

Mendaki bukit tidak serta merta menemukan maksimum global, tetapi mungkin bertemu pada maksimum lokal. Masalah ini tidak terjadi jika heuristiknya cembung. Namun, karena banyak fungsi pendakian bukit yang tidak cembung mungkin sering gagal mencapai maksimum global. Algoritme pencarian lokal lainnya mencoba mengatasi masalah ini seperti pendakian bukit stokastik, jalan acak, dan anil simulasi.

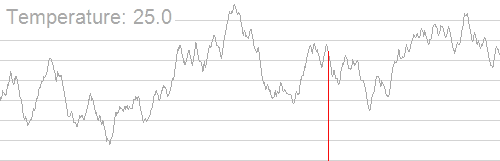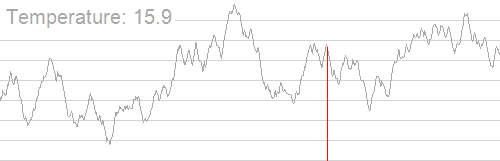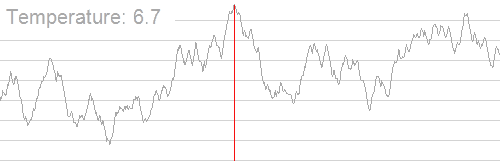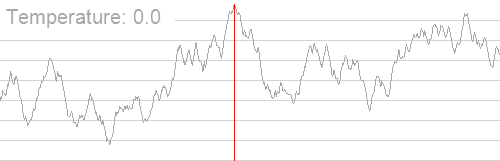
Meskipun banyak maxima lokal dalam grafik ini, maksimum global masih dapat ditemukan dengan menggunakan simulasi annealing. Sayangnya, penerapan simulasi anil adalah masalah khusus karena bergantung pada penemuan lompatan keberuntungan yang meningkatkan posisi. Dalam contoh ekstrem seperti itu, pendakian bukit kemungkinan besar akan menghasilkan maksimum lokal.

Pegunungan dan gang

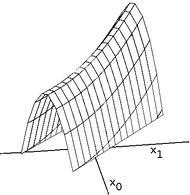
Sebuah punggungan

Punggungan adalah masalah yang menantang bagi pemanjat bukit yang mengoptimalkan dalam ruang terus menerus. Karena pemanjat bukit hanya menyesuaikan satu elemen dalam vektor pada satu waktu, setiap langkah akan bergerak dalam arah yang sejajar sumbu. Jika fungsi target membuat punggungan sempit yang menanjak ke arah yang tidak searah sumbu (atau jika tujuannya adalah meminimalkan, gang sempit yang menurun ke arah yang tidak searah sumbu), maka pemanjat bukit hanya dapat mendaki punggung bukit (atau menuruni gang) dengan zig-zag. Jika sisi punggung bukit (atau gang) sangat curam, maka pemanjat bukit mungkin terpaksa mengambil langkah yang sangat kecil karena zig-zag menuju posisi yang lebih baik. Dengan demikian, mungkin diperlukan waktu yang tidak masuk akal untuk naik ke punggung bukit (atau menuruni gang).

Sebaliknya, metode penurunan gradien dapat bergerak ke segala arah sehingga punggung bukit atau gang dapat naik atau turun. Oleh karena itu, penurunan gradien atau metode gradien konjugasi umumnya lebih disukai daripada mendaki bukit ketika fungsi target dapat dibedakan. Akan tetapi, pemanjat bukit memiliki keuntungan karena tidak memerlukan fungsi target yang dapat dibedakan, sehingga pemanjat bukit mungkin lebih disukai bila fungsi targetnya kompleks.

Dataran

Masalah lain yang terkadang terjadi dengan pendakian bukit adalah dataran tinggi. Dataran tinggi ditemui ketika ruang pencarian datar, atau cukup datar sehingga nilai yang dikembalikan oleh fungsi target tidak dapat dibedakan dari nilai yang dikembalikan untuk wilayah terdekat karena presisi yang digunakan oleh mesin untuk mewakili nilainya. Dalam kasus seperti itu, pemanjat bukit mungkin tidak dapat menentukan ke arah mana ia harus melangkah, dan mungkin mengembara ke arah yang tidak pernah mengarah pada perbaikan.

Sumber Artikel: en.wikipedia.org