Teknik Industri

Memahami Pembelajaran Tanpa Pengawasan (Unsupervised Learning) dalam Jaringan Saraf Tiruan

Dipublikasikan oleh Muhammad Ilham Maulana pada 03 April 2024

Pembelajaran tanpa pengawasan (unsupervised learning) adalah sebuah metode dalam pembelajaran mesin di mana algoritma belajar pola-pola secara ekslusif dari data yang tidak berlabel. Tujuannya adalah melalui peniruan (mimicry), yang merupakan mode pembelajaran penting pada manusia, mesin dipaksa untuk membangun representasi yang ringkas tentang dunianya dan kemudian menghasilkan konten imajinatif darinya.

Metode lain dalam spektrum pengawasan adalah Pembelajaran Penguatan (Reinforcement Learning) di mana mesin hanya diberikan skor kinerja numerik sebagai panduan, dan Pembelajaran Lemah atau Semi-Pengawasan di mana sebagian kecil data diberi label, dan Pembelajaran Kendali Sendiri (Self-Supervision).

Tugas vs. Metode dalam Jaringan Saraf Tiruan 

Tugas jaringan saraf tiruan sering dikategorikan sebagai diskriminatif (pengenalan) atau generatif (imajinasi). Meskipun tidak selalu, tugas diskriminatif cenderung menggunakan metode pembelajaran terbimbing, sedangkan tugas generatif menggunakan pembelajaran tanpa pengawasan. Namun, pemisahan ini sangat kabur. Misalnya, pengenalan objek cenderung menggunakan pembelajaran terbimbing, tetapi pembelajaran tanpa pengawasan juga dapat mengelompokkan objek ke dalam kelompok. Selain itu, seiring kemajuan, beberapa tugas menggunakan kombinasi kedua metode, dan beberapa tugas beralih dari satu metode ke metode lainnya. Sebagai contoh, pengenalan gambar awalnya sangat bergantung pada pembelajaran terbimbing, tetapi kemudian menjadi hibrida dengan menggunakan pra-pelatihan tanpa pengawasan, dan akhirnya kembali ke metode terbimbing dengan munculnya dropout, ReLU, dan learning rate adaptif.

Proses Pelatihan 

Selama fase pembelajaran, jaringan tanpa pengawasan berusaha meniru data yang diberikan dan menggunakan kesalahan dalam hasil tiru-tiruan untuk memperbaiki diri sendiri (yaitu, memperbaiki bobot dan biasnya). Terkadang kesalahan diekspresikan sebagai probabilitas rendah bahwa output yang salah terjadi, atau mungkin diekspresikan sebagai keadaan energi tinggi yang tidak stabil dalam jaringan.

Berbeda dengan metode terbimbing yang mendominasi penggunaan backpropagation, pembelajaran tanpa pengawasan juga menggunakan metode lain termasuk: Aturan Pembelajaran Hopfield, Aturan Pembelajaran Boltzmann, Contrastive Divergence, Wake Sleep, Inferensi Variasional, Maximum Likelihood, Maximum A Posteriori, Gibbs Sampling, dan backpropagating reconstruction errors atau hidden state reparameterizations.

Energ 

Sebuah fungsi energi adalah ukuran makroskopik dari keadaan aktivasi jaringan. Dalam mesin Boltzmann, fungsi ini memainkan peran sebagai Fungsi Biaya. Analogi dengan fisika ini terinspirasi oleh analisis Ludwig Boltzmann tentang energi makroskopik gas dari probabilitas mikroskopik gerakan partikel {\displaystyle p\propto e^{-E/kT}}, di mana k adalah konstanta Boltzmann dan T adalah suhu. Dalam jaringan RBM, relasinya adalah {\displaystyle p=e^{-E}/Z}, di mana {\displaystyle p} dan {\displaystyle E} bervariasi di setiap pola aktivasi yang mungkin dan {\displaystyle \textstyle {Z=\sum _{\scriptscriptstyle {\text{All Patterns}}}e^{-E({\text{pattern}})}}}. Untuk lebih jelas, {\displaystyle p(a)=e^{-E(a)}/Z}, di mana {\displaystyle a} adalah pola aktivasi semua neuron (terlihat dan tersembunyi). Oleh karena itu, beberapa jaringan saraf awal dinamakan Mesin Boltzmann. Paul Smolensky menyebut {\displaystyle -E\,} sebagai Harmoni. Sebuah jaringan mencari energi rendah yang berarti Harmoni tinggi.

Jenis-Jenis Jaringan 

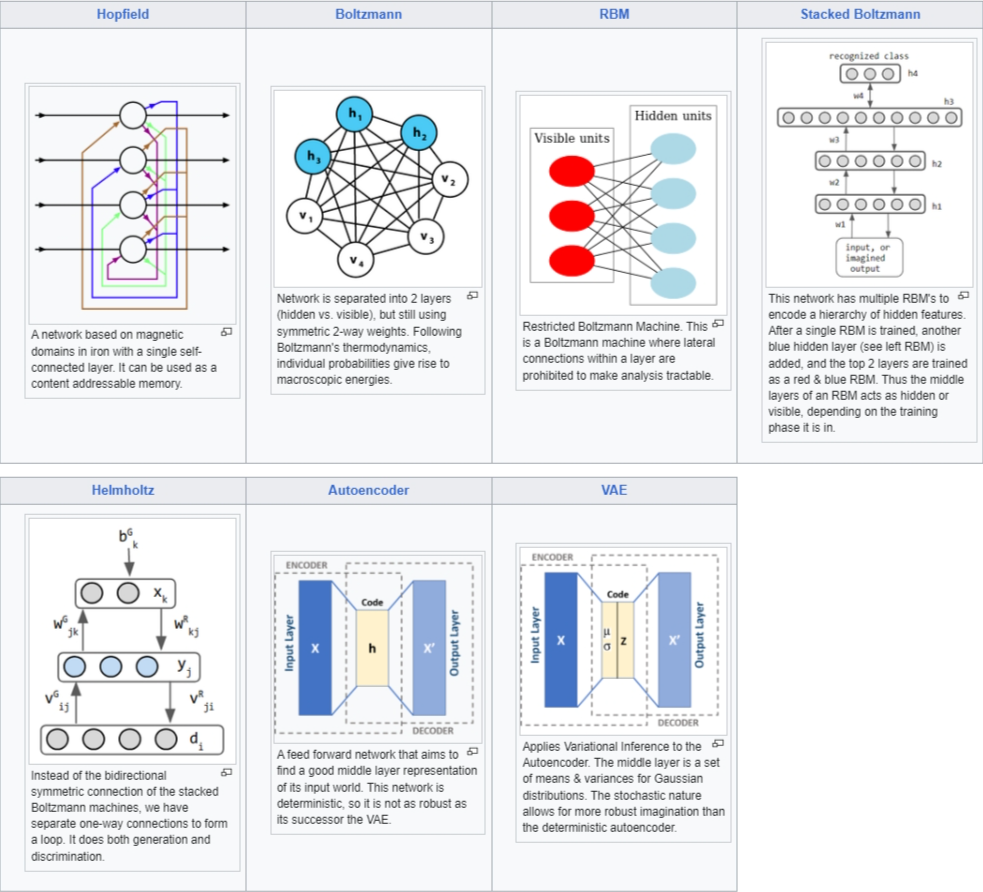
Artikel ini menyajikan diagram koneksi berbagai jaringan tanpa pengawasan, di mana detail akan diberikan dalam bagian Perbandingan Jaringan. Lingkaran mewakili neuron dan tepi di antaranya adalah bobot koneksi. Seiring perubahan desain jaringan, fitur ditambahkan untuk memungkinkan kemampuan baru atau dihilangkan untuk mempercepat pembelajaran. Misalnya, neuron berubah antara deterministik (Hopfield) dan stokastik (Boltzmann) untuk memungkinkan output yang kuat, bobot dihilangkan dalam satu lapisan (RBM) untuk mempercepat pembelajaran, atau koneksi diizinkan menjadi asimetris (Helmholtz).

Contoh gambar.

Dalam dunia pembelajaran mesin, pembelajaran tanpa pengawasan (unsupervised learning) memegang peran penting dalam mengekstraksi pola dan struktur tersembunyi dari data tanpa label. Artikel ini akan mengeksplorasi beberapa metode dan jaringan yang digunakan dalam pembelajaran tanpa pengawasan, serta memberikan gambaran tentang perkembangan historisnya.

Sejarah Singkat:

  • 1969: Perceptrons oleh Minsky & Papert menunjukkan bahwa perceptron tanpa lapisan tersembunyi gagal pada masalah XOR.
  • 1974: Model magnetik Ising diusulkan oleh WA Little untuk kognisi.
  • 1980: Fukushima memperkenalkan neocognitron, yang kemudian disebut jaringan konvolusi, banyak digunakan dalam pembelajaran terbimbing.
  • 1982: Varian Ising, Jaringan Hopfield, dijelaskan sebagai CAM (Content Addressable Memory) dan pengklasifikasi oleh John Hopfield.
  • 1983: Varian Ising lain, Mesin Boltzmann dengan neuron probabilistik, diperkenalkan oleh Hinton & Sejnowski.
  • 1986: Paul Smolensky menerbitkan Teori Harmoni, yang merupakan RBM dengan fungsi energi Boltzmann yang praktis sama.
  • 1995: Schmidthuber memperkenalkan neuron LSTM untuk bahasa.
  • 1995: Dayan & Hinton memperkenalkan Mesin Helmholtz.
  • 2013: Kingma, Rezende, & co. memperkenalkan Variational Autoencoder sebagai jaringan probabilitas grafis Bayesian dengan neural network sebagai komponen.

Jenis-Jenis Jaringan:

  1. Jaringan Hopfield: Terinspirasi dari feromagnetisme, neuron menyerupai domain besi dengan momen magnetik biner. Koneksi simetris memungkinkan formulasi energi global.
  2. Mesin Boltzmann: Varian stokastik dari Jaringan Hopfield, di mana nilai state diambil dari pdf Bernoulli.
  3. Sigmoid Belief Net: Menerapkan ide dari model grafis probabilistik ke neural network. Jaringannya adalah grafik asiklik berarah yang jarang terhubung dengan neuron stokastik biner.
  4. Deep Belief Network: Hibrida dari RBM dan Sigmoid Belief Network, dengan dua lapisan teratas adalah RBM dan lapisan bawah membentuk sigmoid belief network.
  5. Mesin Helmholtz: Kombinasi dua jaringan dalam satu - bobot maju untuk pengenalan dan bobot mundur untuk imajinasi. Inspirasi awal untuk Variational Auto Encoders.
  6. Variational Autoencoder: Terinspirasi oleh Mesin Helmholtz, menggabungkan jaringan probabilitas dengan neural network. Encoder sebagai distribusi probabilitas dan decoder sebagai jaringan neural.

Metode Lainnya:

  • Pembelajaran Hebbian: Prinsip bahwa neuron yang memicu bersama akan terhubung, mendasari fungsi kognitif seperti pengenalan pola dan pembelajaran pengalaman.
  • Self-Organizing Map (SOM) dan Adaptive Resonance Theory (ART) adalah model neural network yang umum digunakan dalam algoritma pembelajaran tanpa pengawasan.
  • Metode probabilistik seperti analisis komponen utama dan kluster digunakan dalam pembelajaran tanpa pengawasan untuk menemukan kesamaan dan kelompok dalam data.
  • Metode momen digunakan untuk mempelajari parameter model variabel laten, seperti dalam pemodelan topik.

Dengan eksplorasi terus-menerus dalam metode pembelajaran tanpa pengawasan, kita dapat meningkatkan kemampuan kecerdasan buatan dalam mengekstraksi wawasan berharga dari data kompleks tanpa label, membuka pintu untuk penemuan dan inovasi baru di berbagai bidang.


Disadur dari: id.wikipedia.org

Selengkapnya
Memahami Pembelajaran Tanpa Pengawasan (Unsupervised Learning) dalam Jaringan Saraf Tiruan

Teknik Industri

Menjelajahi Regresi Linier dalam Statistika: Memahami Hubungan Antar Variabel

Dipublikasikan oleh Muhammad Ilham Maulana pada 01 April 2024

Dalam statistik, regresi linear adalah model statistik yang memperkirakan hubungan linear antara respons skalar dan satu atau lebih variabel penjelas (juga dikenal sebagai variabel terikat dan independen). Kasus satu variabel penjelas disebut regresi linear sederhana; untuk lebih dari satu, prosesnya disebut regresi linear berganda. Istilah ini berbeda dari regresi linear multivariat, di mana beberapa variabel terikat yang berkorelasi diprediksi, bukan hanya satu variabel skalar. Jika variabel penjelas diukur dengan kesalahan, maka diperlukan model kesalahan dalam variabel, juga dikenal sebagai model kesalahan pengukuran.

Dalam regresi linear, hubungan dimodelkan menggunakan fungsi prediktor linear yang parameter modelnya tidak diketahui dan diestimasi dari data. Model-model seperti itu disebut model linear. Paling umum, rata-rata bersyarat respons yang diberikan nilai variabel penjelas (atau prediktor) diasumsikan sebagai fungsi afinitas dari nilai-nilai tersebut; kurang umum, median bersyarat atau beberapa kuantil lainnya digunakan. Seperti semua bentuk analisis regresi, regresi linear berfokus pada distribusi probabilitas bersyarat respons yang diberikan nilai-nilai prediktor, bukan pada distribusi probabilitas bersama dari semua variabel ini, yang merupakan domain analisis multivariat.

Regresi linear adalah jenis analisis regresi pertama yang dipelajari secara ketat dan digunakan secara luas dalam aplikasi praktis. Ini karena model yang bergantung secara linear pada parameter yang tidak diketahui lebih mudah disesuaikan daripada model yang berkaitan secara non-linear dengan parameter mereka dan karena properti statistik estimator yang dihasilkan lebih mudah ditentukan.

Regresi linear memiliki banyak aplikasi praktis. Kebanyakan aplikasi dapat dikategorikan dalam salah satu dari dua kategori umum berikut:

  • Jika tujuannya adalah pengurangan kesalahan yaitu reduksi varians dalam prediksi atau peramalan, regresi linear dapat digunakan untuk memasangkan model prediktif ke suatu himpunan data yang diamati dari nilai respons dan variabel penjelas. Setelah mengembangkan model tersebut, jika nilai tambahan dari variabel penjelas dikumpulkan tanpa nilai respons yang menyertainya, model yang disesuaikan dapat digunakan untuk membuat prediksi respons.
  • Jika tujuannya adalah menjelaskan variasi dalam variabel respons yang dapat dikaitkan dengan variasi dalam variabel penjelas, analisis regresi linear dapat diterapkan untuk mengkuantifikasi kekuatan hubungan antara respons dan variabel penjelas, dan khususnya untuk menentukan apakah beberapa variabel penjelas mungkin tidak memiliki hubungan linear sama sekali dengan respons, atau untuk mengidentifikasi subset variabel penjelas yang mungkin mengandung informasi yang tidak diperlukan tentang respons.

Model-model regresi linear sering dipasangkan menggunakan pendekatan kuadrat terkecil, tetapi mereka juga dapat dipasangkan dengan cara lain, seperti dengan meminimalkan "kurang sesuaian" dalam beberapa norm lain (seperti regresi deviasi terkecil), atau dengan meminimalkan versi berpenalitas dari fungsi biaya kuadrat terkecil seperti pada regresi ridge (penalitas norma L2) dan lasso (penalitas norma L1). Penggunaan Mean Squared Error (MSE) sebagai biaya pada dataset yang memiliki banyak pencilan besar, dapat menghasilkan model yang lebih cocok dengan pencilan daripada data yang sebenarnya karena pentingnya yang lebih tinggi yang diberikan oleh MSE kepada kesalahan besar. Jadi, fungsi biaya yang tangguh terhadap pencilan harus digunakan jika dataset memiliki banyak pencilan besar. Sebaliknya, pendekatan kuadrat terkecil dapat digunakan untuk memasangkan model yang bukan model linear. Dengan demikian, meskipun istilah "kuadrat terkecil" dan "model linear" erat kaitannya, mereka tidak sinonim.

Rumus Sederhana Regresi Linier

Dalam suatu set data {\displaystyle \{y_{i},\,x_{i1},\ldots ,x_{ip}\}_{i=1}^{n}} dari n unit statistik, model regresi linear mengasumsikan bahwa hubungan antara variabel dependen y dan vektor regresor x adalah linear. Hubungan ini dimodelkan melalui istilah gangguan atau variabel error ε — sebuah variabel acak yang tidak diamati yang menambah "noise" pada hubungan linear antara variabel dependen dan regresor. Dengan demikian, model ini memiliki bentuk sebagai berikut.

{\displaystyle y_{i}=\beta _{0}+\beta _{1}x_{i1}+\cdots +\beta _{p}x_{ip}+\varepsilon _{i}=\mathbf {x} _{i}^{\mathsf {T}}{\boldsymbol {\beta }}+\varepsilon _{i},\qquad i=1,\ldots ,n,}

dimana T menunjukkan transpos, sehingga xiTβ adalah produk dalam antara vektor xi dan β.

Seringkali n persamaan ini ditumpuk dan ditulis dalam notasi matriks sebagai

{\displaystyle \mathbf {y} =\mathbf {X} {\boldsymbol {\beta }}+{\boldsymbol {\varepsilon }},\,}

dimana, 

{\displaystyle \mathbf {y} ={\begin{bmatrix}y_{1}\\y_{2}\\\vdots \\y_{n}\end{bmatrix}},\quad }

{\displaystyle \mathbf {X} ={\begin{bmatrix}\mathbf {x} _{1}^{\mathsf {T}}\\\mathbf {x} _{2}^{\mathsf {T}}\\\vdots \\\mathbf {x} _{n}^{\mathsf {T}}\end{bmatrix}}={\begin{bmatrix}1&x_{11}&\cdots &x_{1p}\\1&x_{21}&\cdots &x_{2p}\\\vdots &\vdots &\ddots &\vdots \\1&x_{n1}&\cdots &x_{np}\end{bmatrix}},}

{\displaystyle {\boldsymbol {\beta }}={\begin{bmatrix}\beta _{0}\\\beta _{1}\\\beta _{2}\\\vdots \\\beta _{p}\end{bmatrix}},\quad {\boldsymbol {\varepsilon }}={\begin{bmatrix}\varepsilon _{1}\\\varepsilon _{2}\\\vdots \\\varepsilon _{n}\end{bmatrix}}.}

Notasi dan terminologi

  • {\displaystyle \mathbf {y} }adalah vektor dari nilai yang diamati{\displaystyle y_{i}\ (i=1,\ldots ,n)} of variabel yang disebut regresi, variabel endogen, variabel respons, variabel target, variabel terukur, variabel kriteria, atau variabel terikat.
  • {\displaystyle \mathbf {X} } dapat dilihat sebagai matriks vektor baris {\displaystyle \mathbf {x} _{i\cdot }} atau vektor kolom berdimensi n {\displaystyle \mathbf {x} _{\cdot j}}, yang dikenal sebagai regressor, variabel eksogen, variabel penjelas, kovariat, variabel masukan, variabel prediktor, atau variabel independen (jangan dikelirukan dengan konsep variabel acak independen).
  • {\displaystyle {\boldsymbol {\beta }}} adal ah suatu {\displaystyle (p+1)} vektor parameter dimensi, di mana 0{\displaystyle \beta _{0}}adalah suku intersep (jika ada yang disertakan dalam model—sebaliknya {\displaystyle {\boldsymbol {\beta }}}adalah dimensi p). Elemen-elemennya dikenal sebagai efek atau koefisien regresi (walaupun istilah terakhir kadang-kadang digunakan untuk memperkirakan dampak). Dalam regresi linier sederhana, p=1, dan koefisiennya dikenal sebagai kemiringan regresi. Estimasi dan inferensi statistik dalam regresi linier berfokus pada β. Elemen vektor parameter ini ditafsirkan sebagai turunan parsial variabel terikat terhadap berbagai variabel bebas.
  • {\displaystyle {\boldsymbol {\varepsilon }}} adalah vektor nilai {\displaystyle \varepsilon _{i}}. Bagian model ini disebut istilah error, istilah gangguan, atau terkadang noise (berbeda dengan "sinyal" yang diberikan oleh model lainnya). Variabel ini mencakup semua faktor lain yang mempengaruhi variabel dependen y selain regressor x. Hubungan antara error term dan regressor, misalnya korelasinya, merupakan pertimbangan penting dalam merumuskan model regresi linier, karena hal ini akan menentukan metode estimasi yang tepat.

Contoh Penggunaan

Pertimbangkan situasi di mana sebuah bola kecil dilemparkan ke udara dan kemudian kita mengukur ketinggiannya hi pada berbagai momen waktu ti. Fisika memberi tahu kita bahwa, dengan mengabaikan hambatan, hubungan tersebut dapat dimodelkan sebagai

{\displaystyle h_{i}=\beta _{1}t_{i}+\beta _{2}t_{i}^{2}+\varepsilon _{i},}

dimana β1 menentukan kecepatan awal bola, β2 sebanding dengan gravitasi standar, dan εi disebabkan oleh kesalahan pengukuran. Regresi linier dapat digunakan untuk memperkirakan nilai β1 dan β2 dari data yang diukur. Model ini non-linier pada variabel waktu, tetapi linier pada parameter β1 dan β2; jika kita mengambil regressor xi = (xi1, xi2) = (ti, ti2), modelnya mengambil bentuk standar.

{\displaystyle h_{i}=\mathbf {x} _{i}^{\mathsf {T}}{\boldsymbol {\beta }}+\varepsilon _{i}.}

  • Regresi Linear Univariate 

Dalam regresi linear univariat, hanya ada satu variabel independen yang terlibat. Karena itu, hanya ada satu variabel input X dan satu variabel output Y. Kedua variabel ini direpresentasikan sebagai sumbu X dan Y pada diagram kartesius. Dalam jenis regresi linear ini, model regresi linear dijelaskan sebagai berikut:

{\displaystyle h_{w}(x)=w_{1}x+w_{0}}

dimana {\displaystyle w}{\displaystyle w} merupakan nilai yang akan dicari sedemikian sehingga nilai {\displaystyle w}{\displaystyle w} menjadi optimal dan {\displaystyle x}{\displaystyle x} merupakan variable bebas atau input. Proses pencarian nilai {\displaystyle w}{\displaystyle w} dapat dilakukan dengan beberapa cara diantaranya dengan menggunakan pendekatan least square, maximum likehood, atau algoritme gradient descent. Pada dasarnya, pencarian nilai {\displaystyle w}{\displaystyle w} dilakukan hingga nilai error yang dihasilkan merupakan nilai yang paling minimal. Fungsi error yang digunakan adalah sebagai berikut.

{\displaystyle E(w)={\frac {1}{2N}}\sum _{i=1}^{N}(h_{w}(x^{i})-t^{i})^{2}}

Dimana {\displaystyle N} merupakan banyaknya data input, {\displaystyle h_{w}(x^{i})} merupakan model regresi linear, dan {\displaystyle t} adalah target output yang seharusnya.

  • Regresi Linear Multivariate

Dalam regresi linear multivariat, tidak hanya ada satu variabel independen yang terlibat, tetapi beberapa variabel independen. Hal ini disebabkan oleh penggunaan input yang memiliki lebih dari satu dimensi. Oleh karena itu, diperlukan model regresi linear yang berbeda dari regresi linear univariat. Model regresi linear multivariat dapat dijelaskan sebagai berikut:

{\displaystyle h_{w}(x)=w_{0}+w_{1}x_{1}+w_{2}x_{2}+\dots +w_{m}x_{m}}

{\displaystyle h_{w}(x)=w_{0}+\sum _{i=0}^{m}w_{i}x_{i}}

Dimana {\displaystyle w} juga merupakan nilai yang akan dicari sedemikian sehingga nilai {\displaystyle w} menjadi optimal dan {\displaystyle x} merupakan variable bebas atau input. Proses pencarian nilai {\displaystyle w} juga masih dapat dilakukan dengan menggunakan cara yang sama dengan regresi linear univariate, yaitu dengan menggunakan pendekatan least square, maximum likehood, atau algoritme gradient descent. Pada dasarnya, pencarian nilai {\displaystyle w} dilakukan hingga nilai error yang didapatkan dari fungsi error merupakan nilai yang paling minimal. Fungsi error yang digunakan masih sama dengan regresi linear univariate.


Disadur dari: id.wikipedia.org

Selengkapnya
Menjelajahi Regresi Linier dalam Statistika: Memahami Hubungan Antar Variabel

Teknik Industri

Mengungkap Harta Karun Pengetahuan dengan Data Mining (Penambangan Data)

Dipublikasikan oleh Muhammad Ilham Maulana pada 28 Maret 2024

Data mining (Penambangan Data) adalah proses penting dalam dunia teknologi yang melibatkan ekstraksi dan penemuan pola-pola dalam kumpulan data besar. Ini melibatkan metode yang berada di persimpangan antara pembelajaran mesin, statistik, dan sistem database. Data mining merupakan subbidang interdisipliner dari ilmu komputer dan statistik yang bertujuan untuk mengekstrak informasi dari kumpulan data dan mengubahnya menjadi struktur yang dapat dipahami untuk penggunaan lebih lanjut. Ini merupakan langkah analisis dalam proses "penemuan pengetahuan dalam basis data" atau KDD. Selain langkah analisis, data mining juga melibatkan aspek manajemen data, preprocessing data, pertimbangan model dan inferensi, metrik menarik, kompleksitas, pengolahan hasil yang ditemukan, visualisasi, dan pembaruan online.

Meskipun disebut sebagai "data mining", tujuan sebenarnya adalah ekstraksi pola dan pengetahuan dari data yang besar, bukan penambangan data itu sendiri. Istilah ini sering digunakan secara luas untuk proses pengolahan informasi besar-besaran serta aplikasi sistem pendukung keputusan komputer, termasuk kecerdasan buatan dan bisnis. Tugas utama dalam data mining adalah analisis semi-otomatis atau otomatis dari jumlah data besar untuk mengekstrak pola-pola menarik yang sebelumnya tidak diketahui, seperti kelompok data, catatan yang tidak biasa, dan ketergantungan. Ini melibatkan penggunaan teknik basis data seperti indeks spasial. Pola-pola ini dapat digunakan dalam analisis lebih lanjut atau dalam pembelajaran mesin dan analisis prediktif. Perbedaan utama antara analisis data dan data mining adalah bahwa analisis data digunakan untuk menguji model dan hipotesis pada dataset, sedangkan data mining menggunakan model statistik dan pembelajaran mesin untuk mengungkap pola-pola tersembunyi dalam jumlah data yang besar.

Istilah terkait seperti data dredging, data fishing, dan data snooping mengacu pada penggunaan metode data mining untuk sampel bagian dari kumpulan data yang lebih besar yang mungkin terlalu kecil untuk membuat inferensi statistik yang dapat diandalkan tentang validitas pola yang ditemukan. Meskipun demikian, metode ini dapat digunakan dalam menciptakan hipotesis baru untuk diuji terhadap populasi data yang lebih besar.

Dengan teknologi yang terus berkembang, data mining tetap menjadi alat yang penting dalam mengungkap pola-pola berharga dari data besar dan kompleks, membantu organisasi dalam pengambilan keputusan yang lebih baik dan mempertahankan keunggulan kompetitif di pasar yang semakin kompetitif.

Asal Usul dan Sejarah Data Mining

Pada tahun 1960-an, para ahli statistik dan ekonom menggunakan istilah seperti "data fishing" atau "data dredging" untuk merujuk pada praktik yang dianggap tidak baik dalam menganalisis data tanpa hipotesis a priori. Istilah "data mining" juga digunakan dengan cara yang sama kritis oleh ekonom Michael Lovell dalam sebuah artikel yang diterbitkan di Review of Economic Studies pada tahun 1983. Lovell mengindikasikan bahwa praktik ini "menyamar di bawah berbagai alias, mulai dari "eksperimen" (positif) hingga "fishing" atau "snooping" (negatif).

Istilah data mining muncul sekitar tahun 1990 dalam komunitas basis data, dengan konotasi yang umumnya positif. Untuk sementara waktu pada tahun 1980-an, frasa "database mining"™, digunakan, tetapi karena telah dilindungi hak cipta oleh perusahaan HNC, yang berbasis di San Diego, untuk memasarkan Database Mining Workstation mereka; para peneliti akhirnya beralih ke data mining. Istilah lain yang digunakan termasuk data archaeology, information harvesting, information discovery, knowledge extraction, dll. Gregory Piatetsky-Shapiro menciptakan istilah "knowledge discovery in databases" untuk workshop pertama tentang topik yang sama (KDD-1989) dan istilah ini menjadi lebih populer di komunitas kecerdasan buatan dan pembelajaran mesin. Namun, istilah data mining menjadi lebih populer di kalangan bisnis dan pers. Saat ini, istilah data mining dan penemuan pengetahuan digunakan secara bergantian.

Latar Belakang Ekstraksi manual pola dari data telah terjadi selama berabad-abad. Metode awal untuk mengidentifikasi pola dalam data termasuk teorema Bayes (abad ke-18) dan analisis regresi (abad ke-19). Proliferasi, keberadaan, dan kekuatan yang meningkat dari teknologi komputer secara dramatis telah meningkatkan kemampuan pengumpulan, penyimpanan, dan manipulasi data. Seiring dengan pertumbuhan ukuran dan kompleksitas set data, analisis data langsung dengan tangan secara bertahap telah digantikan dengan pemrosesan data otomatis, dibantu oleh penemuan-penemuan lain dalam ilmu komputer, khususnya dalam bidang pembelajaran mesin, seperti jaringan saraf, analisis klaster, algoritma genetika (tahun 1950-an), pohon keputusan dan aturan keputusan (tahun 1960-an), dan mesin vektor dukungan (tahun 1990-an).

Data mining adalah proses menerapkan metode-metode ini dengan tujuan untuk mengungkap pola tersembunyi dalam set data yang besar. Ini memperjembatani kesenjangan antara statistik terapan dan kecerdasan buatan (yang biasanya menyediakan latar belakang matematika) dengan manajemen basis data dengan memanfaatkan cara data disimpan dan diindeks dalam basis data untuk menjalankan algoritma pembelajaran dan penemuan aktual secara lebih efisien, memungkinkan metode-metode tersebut diterapkan pada set data yang semakin besar.

Proses Penemuan Pengetahuan dari Data

Proses penemuan pengetahuan dari basis data (Knowledge Discovery in Databases/KDD) adalah langkah penting dalam memanfaatkan potensi data. Terdapat beberapa pendekatan seperti CRISP-DM yang menguraikan tahapan-tahapan yang harus diikuti, mulai dari pemahaman bisnis hingga implementasi model. Sebelum melakukan data mining, langkah pra-pemrosesan diperlukan untuk membersihkan data dari noise dan data hilang.

Data mining melibatkan tugas-tugas seperti deteksi anomali, pembelajaran aturan asosiasi, dan klasifikasi, dengan tujuan untuk mengekstrak pola dari data. Namun, hasil dari proses ini harus divalidasi secara hati-hati untuk memastikan keandalan dan kebergunaan informasi yang dihasilkan.

Dengan menggunakan kerangka kerja yang tepat dan melakukan validasi yang cermat, organisasi dapat mengubah data menjadi pengetahuan yang berharga untuk mendukung pengambilan keputusan yang lebih baik.

Proses Pencarian Pola

Penggalian data adalah salah satu bagian dari proses pencarian pola. Berikut ini urutan proses pencarian pola:

  • Pembersihan Data: yaitu menghapus data pengganggu (noise) dan mengisi data yang hilang.
  • Integrasi Data: yaitu menggabungkan berbagai sumber data.
  • Pemilihan Data: yaitu memilih data yang relevan.
  • Transformasi Data: yaitu mentransformasi data ke dalam format untuk diproses dalam penggalian data.
  • Penggalian Data: yaitu menerapkan metode cerdas untuk ekstraksi pola.
  • Evaluasi pola: yaitu mengenali pola-pola yang menarik saja.
  • Penyajian pola: yaitu memvisualisasi pola ke pengguna.

Teknik Penggalian Data

Penggalian data umumnya dapat dibagi menjadi dua fungsi utama: deskripsi dan prediksi. Berikut adalah beberapa fungsi penggalian data yang sering digunakan:

  1. Karakterisasi dan Diskriminasi: Merupakan proses generalisasi, rangkuman, dan perbandingan karakteristik data.
  2. Penggalian Pola Berulang: Melibatkan pencarian pola asosiasi, pola intra-transaksi, atau pola pembelian dalam satu transaksi.
  3. Klasifikasi: Memanfaatkan model untuk mengklasifikasikan objek berdasarkan atribut-atributnya. Kelas target sudah ditentukan sebelumnya dalam data, sehingga fokusnya adalah pada pembelajaran model agar dapat melakukan klasifikasi sendiri.
  4. Prediksi: Memproyeksikan nilai yang tidak diketahui atau nilai yang hilang menggunakan model dari klasifikasi.
  5. Penggugusan/Cluster Analysis: Mengelompokkan objek data berdasarkan tingkat kemiripannya. Kelas target tidak ditentukan sebelumnya dalam data, sehingga tujuannya adalah untuk memaksimalkan kemiripan dalam kelompok dan meminimalkan kemiripan antar kelompok.
  6. Analisis Outlier: Proses identifikasi data yang tidak sesuai dengan pola umum dari data lainnya, seperti noise dan anomali dalam data.
  7. Analisis Trend dan Evolusi: Termasuk analisis regresi, penggalian pola sekuensial, analisis periodisitas, dan analisis berbasis tren.

 

Disadur dari: id.wikipedia.org

Selengkapnya
Mengungkap Harta Karun Pengetahuan dengan Data Mining (Penambangan Data)

Teknik Industri

Apa Itu Industri Manufaktur? - diklatkerja

Dipublikasikan oleh Mochammad Reichand Qolby pada 24 Oktober 2022

Apa Itu Industri Manufaktur?

Industri manufaktur merupakan sebuah badan usaha atau perusahaan untuk memproduksi sebuah barang jadi dari mulain bahan baku mentah yang belum diolah. Sehingga industri ini mempunyai alat, peralatan, mesin produksi dan sebagaimana mestinya untuk memproduksi sebuah bahan baku.

Setelah bahan baku yang sudah diolah tersebut menjadi sebuah produk, barang tersebut akan di pasarkan kepada konsumen melalui jaringan distribusi dari tingkat grosir hingga ke tingkat eceran sampai ke tangan konsumen.

Perusahaan manufaktur atau bisa disebut juga sebagai perusahaan perakitan yang biasanya digunakan oleh industri otomotif maupun elektronik.

Perusahaan manufaktur sangat didukung oleh negara karena dapat memiliki lapangan kerja yang banyak, perusahaan manufakur memiliki peraturan SOP yang harus memiliki standar dan ketat. Hal ini untuk menjaga kualitas sebuah barang atau produk yang dibuat dan diproduksi masal.

Beberapa contoh perusahaan manufaktur :

1. Industri otomotif

2. Industri mesin

3. Industri logam

4. Industri farmasi

5. Industri tekstil

6. Industri rokok

7. Industri barang konsumsi

 

Sumber : money.kompas.com

Selengkapnya
Apa Itu Industri Manufaktur? - diklatkerja

Teknik Industri

Apa Itu Industri Kecil? - diklatkerja

Dipublikasikan oleh Mochammad Reichand Qolby pada 21 Oktober 2022

Industri Kecil

Industri kecil merupakan sebuah bagian usaha yang biasa dilakukan oleh perseorangan. Usaha perseorangan merupakan salah satu badan usaha yang biasa dimiliki oleh satu orang. Biasanya jenis usaha ini ini membutuhkan teknologi yang bagus walaupun hanya dengan modal yang sedikit.

Jenis usaha ini biasanya menerapkan sistem dagang dan jasa. Industri kecil fokus pada barang dan pelayanan jasa pada konsumen dikarenakan sebuah industri kecil harus memiliki kedekatan dengan konsumen. Jenis usaha industri kecil tidak harus memiliki jumlah tenaga kerja yang tidak terlalu banyak. Tenaga kerja biasanya diambil dari lingkungan terdekat dari pemilik. 

Peluang bisnis ini sangat memiliki potensial karena banyak cara untuk melakukan bisnis ataupun usaha industri kecil ini. 

Jenis Industri Kecil

1. Industri Kecil Tradisional

Industri ini biasanya terletak pada daerah pedesaan, teknologi yang digunakan pun relatif sederhana dan penjualan maupun pemasarannya terbatas karena di lingkungan yang lumayan jauh dari pasar. 

2. Industri Kecil Modern

Melibatkan sistem produksi menengah dengan pemasaran domestik maupun impor, teknologi yang bagus dan canggih, dan industi bisa terletak daerah pedesaan maupun perkotaan namun dengan pemasaran dan sistem transportasi yang baik. 

Sumber : bobo.grid.id

Selengkapnya
Apa Itu Industri Kecil? - diklatkerja

Teknik Industri

10 Peluang Profesi Jurusan Teknik Industri - diklatkerja

Dipublikasikan oleh Mochammad Reichand Qolby pada 20 Oktober 2022

10 Peluang Profesi Teknik Industri

Lulusan pada Jurusan Teknik Industri memiliki peluang kerja yang sangat luas. Hal ini bisa mencakup pertambangan, perbankan, periklanan, layanan kesehatan, hingga otomotif untuk menggunakan sebuah tenaga ahli dari jurusan Teknik Industri. Berikut profesi yang bisa diraih oleh lulusan Teknik Industri.

1. Product Analyst

Pada Product Analyst seorang pekerja dapat menganalisa produk, memperhatikan kualitas produksi, optimalkan alat produksi, mengendalikan produksi hingga menjadi keseluruhan produksi. Nantinya analisa dari pekerjaan ini akan dijadikan sebagai efisiensi dan efektivitas produksi suatu industri. 

2. Engineering Manager

Dalam pekerjaan ini seorang Engineer Manager dapat membuat rencana kerja dan mengatur sumber daya yang dibutuhkan dalam suatu proyek kerja. 

3. Project Management Analyst

Project Manager berguna untuk menganalisa efesiensi proses dalam produksi sebuah produk. 

4. Project Manager

Dalam pekerjaan ini tanggung jawab adalah hal yang penting secara bersangkutan dengan Engineering Manager. Namun, pekerjaan yang dilakukan mencakup wilayah yang lebih besar.

5. Sales Engineer

Pekerjaan ini memiliki pengetahuan dalam bidang teknik dan bisnis Teknik Industri. Seorang Sales Engineer harus memiliki product knowledge yang baik dan mampu menjelaskan keseluruhan produk yang telah dihasilkan oleh perusahaan.

6. Cost Control Engineer

Cost Control Engineer berguna untuk mengkakulasikan biaya, tenaga dan waktu yang diperlukan dalam menjalankan sebuah produksi.

7. Health and Safety Environment Engineer

Tugas dalam pekerjaan ini adalah menganalisa sebuah prosedur kerja dan lokasi yang akan berdampak pada keselamatan dan kesehatan kerja.

8. Quality Control Engineer

Pekerjaan ini merupakan sebuah akhir dari proses produksi, pekerjaan ini harus memastikan bahwa semua produk final telah memenuhi standar kualitas yang telah ditentukan.

9. Logistic Specialist

Pekerjaan ini merupakan sebuah penganalisaan dan mengatur rantai pasokan produksi.

10. Konsultan

Lulusan Teknik Industri akan mempunyai skill berpikir secara sistematik dan integratif, sehingga lulusan dari Teknik Industri cocok untuk dibutuhkan menjadi seorang konsultan. 

Sumber : akupintar.id

Selengkapnya
10 Peluang Profesi Jurusan Teknik Industri - diklatkerja
« First Previous page 74 of 75 Next Last »