Model linier umum
Model linier umum atau model regresi multivariat adalah cara mudah untuk membangun beberapa model regresi linier sekaligus. Dalam hal ini, ini bukanlah model statistik yang unik. Beberapa model regresi linier dapat diringkas sebagai berikut:
dimana Y adalah matriks yang berisi sekumpulan beberapa ukuran (setiap kolom adalah kumpulan ukuran untuk salah satu variabel terikat), biasanya berisi parameter estimasi, dan U adalah matriks yang berisi kesalahan (kebisingan). Umumnya diasumsikan terdapat kesalahan antar pengukuran dan mengikuti distribusi normal multivariat. Jika kesalahan tidak mengikuti distribusi normal multivariat,
Anda dapat melonggarkan asumsi tentang Y dan U menggunakan model linier umum.Anda dapat menggunakan model linier umum dan berbagai model statistik, termasuk ANOVA, ANCOVA, MANOVA, MANCOVA, dan regresi linier umum. menyatukannya , uji t, dan uji F. Generalized linear modelling merupakan gambaran regresi linier berganda ketika terdapat lebih dari dua variabel terikat. Jika Y, B, dan U adalah vektor kolom, persamaan matriks di atas mewakili regresi linier berganda.
Hipotesis dapat diuji dengan model linier umum dengan dua cara: uji varians atau uji varians independen berganda. kamu bisa Dalam pengujian berganda, kolom Y diuji, tetapi dalam pengujian tunggal, kolom Y diuji. Artinya, banyak pengujian berbeda dilakukan dengan menggunakan matriks desain yang sama.
Perbandingan dengan regresi linier berganda
Regresi linier berganda merupakan perluasan dari regresi linier sederhana untuk dua atau lebih variabel bebas dan merupakan kasus khusus untuk model linier umum yang terbatas pada satu variabel terikat. Rumus dasar regresi linier berganda adalah:
untuk setiap pengamatan i = 1, ... , n.
Model di atas mempertimbangkan n observasi variabel terikat dan p variabel bebas. Jadi, Yi adalah observasi ke-i terhadap variabel terikat, Xij adalah observasi ke-i terhadap variabel bebas ke-j, dan j = 1, 2, ..., p. Nilai j mewakili parameter yang akan diestimasi dan i adalah distribusi kesalahan normal independen.
Regresi linier berganda memiliki persamaan seperti di atas untuk setiap variabel m > 1. keyakinan. Karena variabel penjelasnya sama, maka variabel tersebut diestimasi secara bersamaan satu sama lain:
untuk semua observasi diindeks sebagai i = 1, ... , n dan untuk semua variabel dependen diindeks sebagai j = 1, ... , m.
Karena setiap variabel terikat memiliki serangkaian parameter regresi yang relevan, dari perspektif komputasi, regresi multivariat umum hanyalah serangkaian regresi linier berganda yang menggunakan variabel penjelas yang sama.
Perbandingan dengan model linier umum
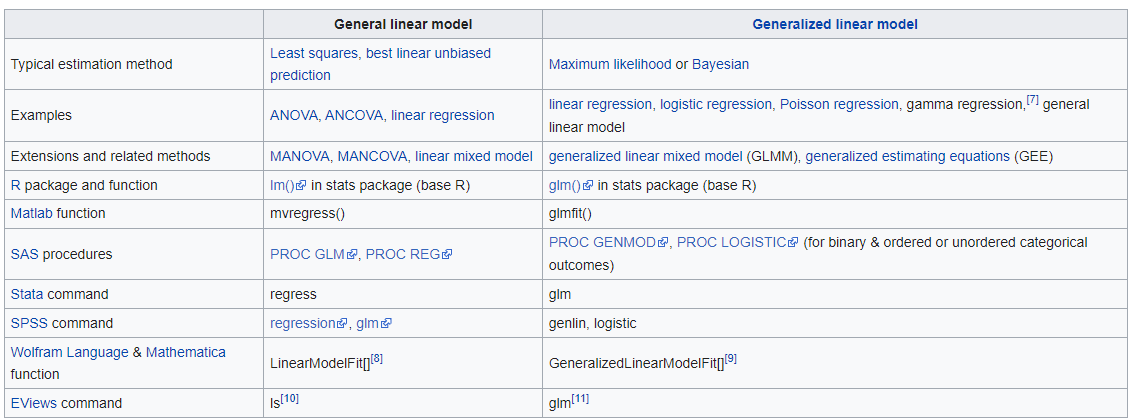
Model linier umum (GLM) dan model linier umum (LM) adalah dua pendekatan statistik yang umum digunakan untuk mengevaluasi hubungan antara beberapa prediktor dan satu variabel hasil. Perbedaan utama antara keduanya terletak pada asumsi distribusi residu.
Model linier umum (LM) mengasumsikan dengan kuat bahwa residu mengikuti distribusi normal bersyarat. Sebaliknya, GLM melonggarkan asumsi ini dan memungkinkan distribusi keluarga eksponensial yang berbeda untuk residunya. Penting untuk dicatat bahwa LM adalah kasus khusus GLM yang mana distribusi residu mengikuti distribusi normal bersyarat.
Distribusi residu sangat dipengaruhi oleh jenis dan distribusi variabel.output. GLM menyediakan model berbeda untuk menyesuaikan variabel hasil yang berbeda. Beberapa contoh umum dalam keluarga GLM mencakup regresi binomial untuk hasil biner atau bivariat, regresi Poisson untuk menghitung hasil, distribusi normal, dan regresi linier untuk keluaran langsung. Oleh karena itu, GLM dianggap sebagai rangkaian model statistik yang luas, atau model yang dapat disesuaikan dengan hasil yang berbeda.
Aplikasi
Penerapan model linier umum muncul dalam analisis beberapa pemindaian otak di bidang eksperimen ilmiah, di mana Y berisi data pemindaian otak dan X berisi variabel desain eksperimen dan faktor perancu. Hal ini biasanya diuji menggunakan multivariat (di sini disebut massa univariat) dan disebut juga peta parameter statistik.
Disadur dari: en.wikipedia.org


