Dalam tutorial ini, kita akan mempelajari algoritma heuristik, metaheuristik, dan probabilistik. Kami akan fokus pada definisi, persamaan, perbedaan, dan contohnya.
Pertama, kita akan memiliki tinjauan singkat tentang pemecahan masalah dan optimasi masalah dalam Ilmu Komputer, sehingga membahas teknik tradisional dalam konteks ini. Jadi, kita akan melihat konsep dan fitur tertentu dari heuristik, metaheuristik, dan algoritma probabilistik. Terakhir, kami akan membandingkannya dalam ringkasan sistematis.
Pemecahan masalah ilmu komputer
Pada dasarnya, kita menggunakan komputasi untuk memecahkan berbagai masalah dunia nyata.
Misalnya, kita dapat menggunakan teori grafik dan algoritma untuk menentukan jalu terpendek dalan jalu tertentu . Selanjutnya, kita dapat menghitung alokasi barang terbaik dalam tas berdasarkan ukuran dan beratnya.
Kedua skenario yang dikutip sebelumnya adalah masalah optimasi klasik dalam Ilmu Komputer yang masing-masing kami sebut “The Traveling Salesman” dan “The Knapsack Problem”.
Untuk mengatasi masalah ini, kita dapat menerapkan beberapa strategi berbeda. Beberapa strategi hanya menyelesaikan satu masalah, sementara strategi lainnya dapat disesuaikan untuk mengatasi banyak masalah.
Selain itu, beberapa strategi mungkin mendapatkan hasil yang optimal secara global. Strategi lain, pada gilirannya, memberikan hasil yang kurang optimal namun cukup baik. Dalam kasus terakhir, kita dapat mengklasifikasikan strategi pemecahan masalah menjadi strategi eksak atau tidak eksak. Mari kita lihat klasifikasinya pada subbagian berikut.
Strategi tepat dan tidak tepat
Seperti yang telah dibahas sebelumnya, kategori eksak dan non eksak memperhatikan kemungkinan suatu strategi pemecahan masalah mendapatkan hasil yang optimal.
Singkatnya, algoritma yang tepat menjamin (dengan probabilitas 100%) pencapaian solusi optimal untuk masalah tertentu. Strategi seperti algoritma brute force selalu tepat.
Selain itu, kami dapat mendukung heuristik untuk algoritma yang tepat. Berdasarkan permasalahan tersebut, kita dapat menggunakan heuristik untuk menghindari pilihan yang buruk dan hanya menguji (dan semua) hasil yang menjanjikan.
Namun, algoritme yang tepat mungkin memerlukan lebih banyak sumber daya komputasi dan waktu eksekusi daripada yang harus kita selesaikan. Dalam kasus seperti ini, strategi yang tidak tepat adalah pilihan terbaik.
Dalam skenario ini, kami bekerja dengan algoritme yang tidak menjamin hasil optimal secara global. Namun, algoritma non-eksak mengeksplorasi masalah dengan cara yang cerdas, sehingga menemukan hasil yang baik dalam waktu yang memungkinkan dengan sumber daya yang lebih sedikit.
Jadi, algoritma heuristik, metaheuristik, dan probabilistik adalah strategi yang tidak eksak. Beberapa contohnya adalah algoritma pencarian masalah , pencarian tabu, dan strategi evolusi.
Pada bagian berikut, kita secara khusus akan melihat konsep dan contoh heuristik, metaheuristik, dan algoritma probabilistik.
Heuristik
Heuristik adalah strategi yang menggunakan informasi tentang masalah yang sedang dipecahkan untuk menemukan solusi yang menjanjikan .
Menurut heuristik yang dipilih untuk suatu masalah tertentu, tujuannya tidak selalu mencari solusi optimal tetapi hanya menemukan solusi yang cukup baik. Heuristik berdasarkan pencarian serakah ada di kelas ini, misalnya.
Di lain waktu, kita dapat menggunakan heuristik bukan untuk menemukan hasil, melainkan membuang hasil yang jelas-jelas buruk. Dalam kasus seperti itu, heuristik menghapus sebagian ruang pencarian dan menguji semua kemungkinan hasil yang tersisa. Kami menyebutnya heuristik pendukung.
Terlepas dari heuristik mana yang kita adopsi, mereka memiliki beberapa karakteristik umum:
- Desain berbasis masalah: heuristik disesuaikan dengan masalah tertentu. Dengan cara ini, heuristik tunggal sering kali hanya dapat menyelesaikan satu masalah, dan tidak lebih (relasi satu-ke-satu)
- Keberhasilan yang tidak dapat diukur: berbeda dengan algoritma perkiraan, heuristik tidak memberikan indikasi yang jelas tentang seberapa dekat (atau jauh) hasil yang diperoleh dengan hasil optimal
- Eksekusi yang wajar: waktu atau sumber daya komputasi untuk mengeksekusi heuristik tidak boleh melebihi persyaratan metode pasti apa pun yang memecahkan masalah yang sama
Gambar berikut menggambarkan bagaimana heuristik berbasis penelusuran yang tepat, mendukung, dan serakah mengatasi masalah penjual keliling yang sederhana:
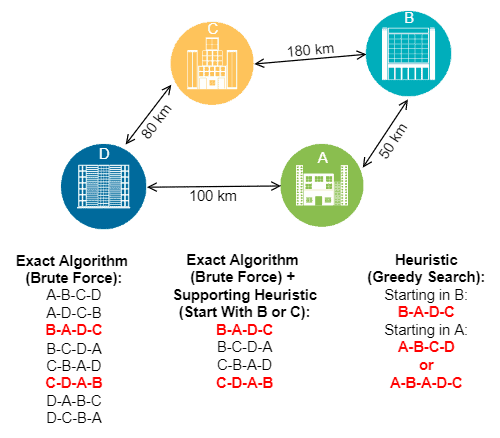
Sumber: baeldung.com
Pada gambar di atas, hasil akhirnya berwarna merah. Jadi, algoritma yang tepat selalu memberikan hasil yang optimal secara global. Algoritma yang tepat dengan heuristik pendukungnya juga menemukan hasil yang optimal secara global. Pada akhirnya, heuristik dapat mengembalikan hasil optimal secara global, namun hal ini bergantung pada parameter yang disediakan untuk eksekusi.
Metaheuristik
Mirip dengan heuristik, metaheuristik bertujuan untuk menemukan hasil yang menjanjikan untuk suatu masalah. Namun, algoritma yang digunakan untuk metaheuristik bersifat umum dan dapat menangani masalah yang berbeda.
Dengan cara ini, karakteristik “keberhasilan yang tidak dapat diukur” dan “eksekusi yang wajar” masih sama seperti yang dibahas dalam heuristik. Namun, metaheuristik menggantikan prinsip desain berbasis masalah dengan desain yang tidak bergantung pada masalah:
- Desain yang tidak bergantung pada masalah: kemungkinan menggunakan algoritma metaheuristik yang sama untuk memecahkan berbagai masalah hanya dengan menyetel masukannya
Contoh metaheuristik yang terkenal adalah algoritma matematika, optimasi kawanan artikel,simulasi anil, dan pencarian lingkungan variabel. Selain itu, menurut cara kerja metaheuristik untuk menemukan hasil suatu masalah, kita dapat membaginya menjadi tiga kategori:
- Metaheuristik pencarian lokal: juga dikenal sebagai perbaikan berulang, metaheuristik dalam kategori ini menemukan hasil akhir yang baik dengan meningkatkan satu hasil antara secara berulang
- Metaheuristik konstruktif: alih-alih menyelesaikan seluruh masalah sekaligus, metaheuristik konstruktif memecah masalah menjadi beberapa submasalah, menyelesaikan masing-masing submasalah, dan menggabungkan hasil parsial untuk memberikan hasil yang lengkap
- Metaheuristik berbasis populasi: kategori metaheuristik ini mempertimbangkan populasi hasil potensial untuk suatu masalah tertentu, sehingga meningkatkan hasil potensial tersebut dengan menggabungkan dan memodifikasinya
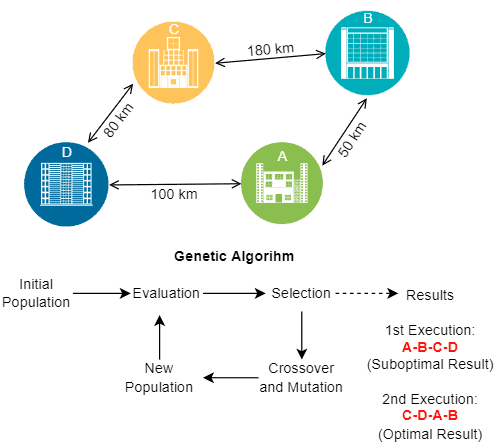
Gambar berikut menunjukkan contoh sederhana masalah travelling salesman yang diselesaikan dengan algoritma genetika, yaitu metaheuristik berbasis populasi:
Sumber: baeldung.com
Penting untuk dicatat bahwa, dalam kasus spesifik metaheuristik genetik, kita tidak dapat menyimpulkan hasil berdasarkan masukan karena terdapat operasi stokastik untuk menentukan kapan dan bagaimana hasil perantara digabungkan dan dimodifikasi.
Algoritma probabilistik
Kita telah membicarakan tentang algoritma heuristik dan metaheuristik yang mengorbankan kepastian menemukan hasil optimal untuk menghasilkan hasil yang cukup baik dengan waktu dan sumber daya komputasi yang layak.
Selain itu, kita secara singkat membahas algoritma eksak (juga dikenal sebagai deterministik) yang selalu memberikan hasil optimal untuk masalah tertentu.
Algoritme probabilistik, pada gilirannya, adalah kelas strategi pemecahan masalah yang tidak eksak. Namun , tidak seperti heuristik dan metaheuristik, algoritma probabilistik dirancang untuk mendapatkan hasil yang optimal.
Namun, algoritma probabilistik hanya memiliki probabilitas tinggi untuk menemukan hasil optimal dalam waktu yang memungkinkan. Jadi, algoritme ini tidak menjamin hasil optimal atau pengurangan waktu eksekusi untuk menemukannya.
Hal ini terjadi karena algoritma probabilistik menggunakan beberapa elemen acak. Jadi, bergantung pada definisi elemen acak ini dalam setiap eksekusi, kita dapat mengubah masalah kompleks menjadi masalah sederhana atau masalah yang sulit diselesaikan.
Ada tiga kategori utama algoritma probabilistik:
- Monte carlo: kami dengan cepat menemukan hasil, tetapi hasilnya mungkin tidak benar atau optimal
- Las vegas: kami menemukan hasil yang optimal atau benar, tetapi tidak ada jaminan cepat untuk melakukannya
- Sherwood: kami selalu menemukan hasil yang optimal atau benar, dan faktor acak menghindari kami melakukan hal itu dengan mengambil skenario eksekusi terburuk
Contoh sederhana monte carlo
Mari kita pertimbangkan daftar angka dan algoritma Monte Carlo untuk memeriksa apakah ada elemen mayoritas (setidaknya 50% + 1 kemunculan) dalam daftar tersebut. Algoritme memilih nomor acak dari daftar dan memeriksa kemunculannya, mengembalikan nilai benar jika angka tersebut merupakan angka mayoritas atau salah jika bukan angka mayoritas.
Pseudocode dari algoritma yang dijelaskan sebagai berikut:
algorithm MonteCarloMajority(numberList, lengthList):
- // INPUT
- // numberList = a list of numbers
- // lengthList = the length of numberList
- // OUTPUT
- Returns true if a randomly selected number appears more than lengthList / 2 times,
- // and false otherwise
- i <- RANDOM() mod lengthList
- // RANDOM() returns a random number
- j <- 0
- c <- 0
- while j < lengthList:
- if numberList[i] = numberList[j]:
- c <- c + 1
- if numberList[i] = numberList[j]:
- j <- j + 1 return c > lengthList / 2
Jadi, jika terdapat elemen mayoritas, kemungkinan mendapatkan hasil yang salah lebih kecil dari . Dengan cara ini, jika kita menjalankan algoritme ini sebanyak N kali dan hasilnya selalu salah, kita meningkatkan keyakinannya dan kemungkinan kesalahannya berkurang menjadi .
Tentu saja, selalu ada kemungkinan adanya jumlah mayoritas. Namun, ketika jumlah eksekusi meningkat dan kami tidak menemukan jumlah mayoritas ini, kemungkinan adanya jumlah tersebut menjadi dapat diabaikan.
Ringkasan sistematis
Saat ini, kami menggunakan sistem komputer untuk memecahkan berbagai masalah. Beberapa permasalahan sederhana jika dilihat dari kemampuan komputasi yang tersedia saat ini. Dalam hal ini, kita dapat menggunakan algoritma yang tepat untuk menyelesaikan masalah ini, sehingga mendapatkan hasil yang optimal.
Namun, masalah lain terlalu rumit untuk diselesaikan dengan algoritma yang tepat dalam waktu yang memungkinkan dan menggunakan sumber daya komputasi yang wajar. Jadi, kita bisa menggunakan strategi kelas lain untuk menyelesaikannya. Contohnya adalah heuristik, metaheuristik, dan algoritma probabilistik.
Kelas algoritme lain ini dapat menemukan hasil optimal untuk suatu masalah, seperti algoritme eksak, namun hal ini tidak dijamin. Namun, algoritme ini lebih cepat dan biasanya mengonsumsi lebih sedikit sumber daya komputasi dibandingkan alternatif lainnya.
Tabel di bawah ini merangkum karakteristik algoritma eksak, heuristik, metaheuristik, dan probabilistik.
Kesimpulan
Dalam tutorial ini, kita mempelajari strategi heuristik, metaheuristik, dan probabilistik. Pada awalnya, kami meninjau secara singkat pemecahan masalah dalam konteks komputasi. Jadi, kami secara khusus mengeksplorasi karakteristik algoritma heuristik, metaheuristik, dan probabilistik. Terakhir, kami membandingkan beberapa karakteristik kelas algoritme yang berbeda ini dalam ringkasan sistematis.
Kita dapat menyimpulkan bahwa strategi non-eksak sangat penting untuk memecahkan masalah komputasi. Namun, ada masalah yang rumit , dan menggunakan algoritma yang tepat untuk menyelesaikannya adalah hal yang tidak mungkin dilakukan. Dengan demikian, algoritma heuristik, metaheuristik, dan probabilistik menjadi pilihan yang tepat untuk memecahkan masalah komputasi yang kompleks ini.
Disadur dari: baeldung.com