Pohon keputusan atau Decision Tree adalah model hierarkis pendukung keputusan yang menggunakan struktur mirip pohon untuk menggambarkan keputusan dan konsekuensi-konsekuensinya, termasuk hasil-hasil dari kejadian kebetulan, biaya sumber daya, dan utilitas. Ini merupakan salah satu cara untuk menampilkan algoritma yang hanya mengandung pernyataan kontrol kondisional.
Pohon keputusan umumnya digunakan dalam riset operasi, khususnya dalam analisis keputusan, untuk membantu mengidentifikasi strategi yang paling mungkin mencapai tujuan, tetapi juga merupakan alat yang populer dalam pembelajaran mesin.
Pohon keputusan adalah struktur mirip bagan alir di mana setiap simpul internal mewakili "tes" pada atribut (misalnya, apakah lemparan koin muncul kepala atau ekor), setiap cabang mewakili hasil dari tes tersebut, dan setiap simpul daun mewakili label kelas (keputusan yang diambil setelah menghitung semua atribut). Jalur dari akar ke daun mewakili aturan klasifikasi.
Dalam analisis keputusan, pohon keputusan dan diagram pengaruh yang terkait erat digunakan sebagai alat bantu keputusan visual dan analitis, di mana nilai-nilai yang diharapkan (atau utilitas yang diharapkan) dari alternatif-alternatif yang bersaing dihitung.
Sebuah pohon keputusan terdiri dari tiga jenis simpul:
- Simpul keputusan – biasanya direpresentasikan oleh kotak
- Simpul kebetulan – biasanya direpresentasikan oleh lingkaran
- Simpul akhir – biasanya direpresentasikan oleh segitiga
Pohon keputusan umumnya digunakan dalam riset operasi dan manajemen operasi. Jika, dalam praktiknya, keputusan harus diambil secara online tanpa pengingat di bawah pengetahuan yang tidak lengkap, sebuah pohon keputusan harus diparalelkan dengan model probabilitas sebagai model pilihan terbaik atau algoritma pemilihan online. Penggunaan lain dari pohon keputusan adalah sebagai sarana deskriptif untuk menghitung probabilitas bersyarat.
Pohon keputusan, diagram pengaruh, fungsi utilitas, dan alat dan metode analisis keputusan lainnya diajarkan kepada mahasiswa sarjana di sekolah-sekolah bisnis, ekonomi kesehatan, dan kesehatan masyarakat, dan merupakan contoh dari metode riset operasi atau ilmu manajemen.
Blok-blok pembangun pohon keputusan (Decision-tree elements)
Elemen pohon keputusan
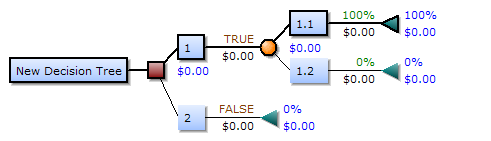
Jika digambar dari kiri ke kanan, sebuah pohon keputusan hanya memiliki simpul-simpul pecah (jalur pembelahan) tetapi tidak memiliki simpul-simpul penyatu (jalur konvergen). Oleh karena itu, jika digunakan secara manual, pohon keputusan dapat menjadi sangat besar dan seringkali sulit untuk digambar sepenuhnya dengan tangan. Secara tradisional, pohon keputusan dibuat secara manual - seperti yang ditunjukkan pada contoh di samping - meskipun semakin banyak digunakan software khusus.
Aturan keputusan (Decision rules)
Pohon keputusan dapat di linearisasikan menjadi aturan keputusan, di mana hasilnya adalah isi dari simpul daun, dan kondisi-kondisi sepanjang jalur membentuk konjungsi dalam klausa if. Secara umum, aturan-aturan tersebut memiliki bentuk:
jika kondisi1 dan kondisi2 dan kondisi3 maka hasilnya. Aturan keputusan dapat dihasilkan dengan membangun aturan asosiasi dengan variabel target di sebelah kanan. Mereka juga dapat menunjukkan hubungan temporal atau kausal.
Pohon keputusan menggunakan flowchart simbol
Biasanya pohon keputusan digambarkan menggunakan simbol-simbol bagan alir karena lebih mudah bagi banyak orang untuk dibaca dan dipahami. Perlu diperhatikan bahwa terdapat kesalahan konseptual dalam perhitungan "Lanjut" dari pohon yang ditunjukkan di bawah ini; kesalahan tersebut terkait dengan perhitungan "biaya" yang diberikan dalam tindakan hukum.
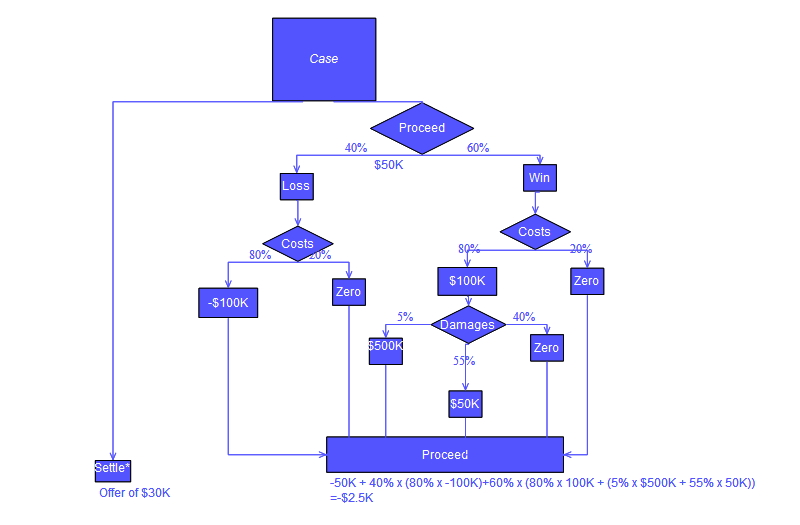
Contoh Analisis
Analisis dapat memperhitungkan preferensi atau fungsi utilitas pengambil keputusan (misalnya, perusahaan), sebagai contoh:
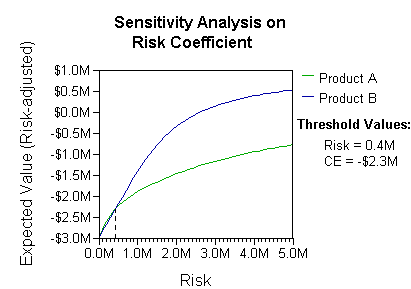
Interpretasi dasar dalam situasi ini adalah bahwa perusahaan lebih memilih risiko dan imbalan dari B dengan koefisien preferensi risiko yang realistis (lebih besar dari $400 ribu - dalam rentang kecenderungan risiko tersebut, perusahaan akan perlu memodelkan strategi ketiga, "Tidak A maupun B").
Contoh lain yang umum digunakan dalam kursus riset operasi adalah distribusi penjaga pantai di pantai-pantai (dikenal sebagai contoh "Life's a Beach"). Contoh tersebut menggambarkan dua pantai dengan penjaga pantai yang akan didistribusikan di setiap pantai. Ada anggaran maksimum B yang dapat didistribusikan di antara kedua pantai (secara total), dan dengan menggunakan tabel pengembalian marjinal, para analis dapat memutuskan berapa banyak penjaga pantai yang dialokasikan ke masing-masing pantai.
Diagram pengaruh (Influence diagram)
Sebagian besar informasi dalam sebuah pohon keputusan dapat direpresentasikan lebih ringkas sebagai diagram pengaruh, yang memfokuskan perhatian pada masalah-masalah dan hubungan antara peristiwa-peristiwa.
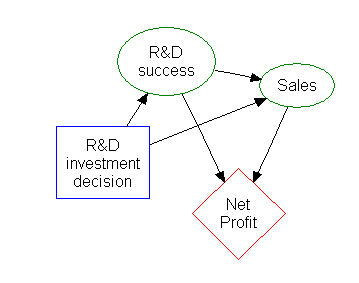
Induksi Aturan Asosiasi
Pohon keputusan juga dapat dilihat sebagai model generatif dari aturan induksi dari data empiris. Sebuah pohon keputusan optimal kemudian didefinisikan sebagai pohon yang memperhitungkan sebagian besar data, sambil meminimalkan jumlah level (atau "pertanyaan"). Beberapa algoritma untuk menghasilkan pohon-pohon optimal tersebut telah dikembangkan, seperti ID3/4/5, CLS, ASSISTANT, dan CART.
Kelebihan dan Kekurangan
Di antara alat bantu keputusan, pohon keputusan (dan diagram pengaruh) memiliki beberapa keunggulan. Pohon keputusan:
- Mudah dipahami dan diinterpretasikan. Orang dapat memahami model pohon keputusan setelah penjelasan singkat.
- Memiliki nilai bahkan dengan sedikit data keras. Insight penting dapat dihasilkan berdasarkan ahli yang menggambarkan situasi (alternatifnya, probabilitas, dan biaya), serta preferensi mereka terhadap hasil.
- Membantu menentukan nilai terburuk, terbaik, dan yang diharapkan untuk berbagai skenario.
- Menggunakan model kotak putih. Jika hasil tertentu diberikan oleh sebuah model.
- Dapat digabungkan dengan teknik keputusan lainnya.
- Tindakan dari lebih dari satu pengambil keputusan dapat dipertimbangkan.
Kekurangan dari pohon keputusan:
- Tidak stabil, yang berarti perubahan kecil dalam data dapat menyebabkan perubahan besar dalam struktur pohon keputusan optimal.
- Seringkali relatif tidak akurat. Banyak prediktor lain memiliki kinerja yang lebih baik dengan data serupa. Hal ini dapat diperbaiki dengan menggantikan satu pohon keputusan dengan hutan acak dari pohon keputusan, tetapi hutan acak tidak sesederhana pohon keputusan tunggal dalam interpretasinya.
- Untuk data yang mencakup variabel kategoris dengan jumlah level yang berbeda, peningkatan informasi dalam pohon keputusan bias dalam mendukung atribut-atribut dengan lebih banyak level.
- Perhitungan dapat menjadi sangat kompleks, terutama jika banyak nilai tidak pasti dan/atau jika banyak hasil terkait.
Optimisasi Pohon Keputusan
Beberapa hal harus dipertimbangkan saat meningkatkan akurasi klasifikasi pohon keputusan. Berikut adalah beberapa optimisasi yang mungkin perlu dipertimbangkan untuk memastikan model pohon keputusan yang dihasilkan membuat keputusan atau klasifikasi yang benar. Perlu dicatat bahwa hal-hal ini bukanlah satu-satunya hal yang perlu dipertimbangkan, tetapi hanya beberapa di antaranya.
Meningkatkan jumlah level pohon
Akurasi pohon keputusan dapat berubah berdasarkan kedalaman pohon keputusan. Dalam banyak kasus, daun pohon adalah simpul murni. Ketika sebuah simpul adalah murni, berarti semua data dalam simpul tersebut termasuk dalam satu kelas. Sebagai contoh, jika kelas-kelas dalam kumpulan data adalah Kanker dan Non-Kanker, sebuah simpul daun akan dianggap murni ketika semua data sampel dalam simpul daun tersebut merupakan bagian dari satu kelas saja, baik kanker atau non-kanker. Perlu diingat bahwa pohon yang lebih dalam tidak selalu lebih baik saat mengoptimalkan pohon keputusan. Pohon yang lebih dalam dapat mempengaruhi waktu eksekusi secara negatif. Jika sebuah algoritma klasifikasi tertentu digunakan, maka pohon yang lebih dalam dapat berarti waktu eksekusi algoritma klasifikasi ini secara signifikan lebih lambat. Ada juga kemungkinan bahwa algoritma yang sebenarnya membangun pohon keputusan akan menjadi lebih lambat secara signifikan seiring dengan kedalaman pohon yang meningkat. Jika algoritma pembangunan pohon yang digunakan membagi simpul murni, maka dapat mengalami penurunan akurasi keseluruhan dari klasifikasi pohon. Kadang-kadang, peningkatan kedalaman pohon dapat menyebabkan penurunan akurasi secara umum, sehingga sangat penting untuk menguji modifikasi kedalaman pohon keputusan dan memilih kedalaman yang menghasilkan hasil terbaik. Untuk merangkum, perhatikan poin-poin di bawah ini, kita akan mendefinisikan jumlah D sebagai kedalaman pohon.
Keuntungan kemungkinan dari peningkatan jumlah D:
- Akurasi model klasifikasi pohon keputusan meningkat.
- Kemungkinan kerugian dari peningkatan D:
- Masalah waktu eksekusi
- Penurunan akurasi secara umum
- Pembagian simpul murni saat semakin dalam bisa menyebabkan masalah.
- Kemampuan untuk menguji perbedaan hasil klasifikasi ketika mengubah D sangat penting. Kita harus dapat dengan mudah mengubah dan menguji variabel-variabel yang dapat memengaruhi akurasi dan keandalan model pohon keputusan.
Pemilihan fungsi pembagian simpul
Fungsi pembagian simpul yang digunakan dapat berdampak pada peningkatan akurasi pohon keputusan. Sebagai contoh, menggunakan fungsi gain informasi mungkin menghasilkan hasil yang lebih baik daripada menggunakan fungsi phi. Fungsi phi dikenal sebagai ukuran "kebaikan" dari pemisahan kandidat di simpul dalam pohon keputusan. Fungsi gain informasi dikenal sebagai ukuran "pengurangan entropi". Pada contoh berikut, kita akan membangun dua pohon keputusan. Satu pohon keputusan akan dibangun menggunakan fungsi phi untuk membagi simpul-simpul dan satu pohon keputusan akan dibangun menggunakan fungsi gain informasi untuk membagi simpul-simpul.
Kelebihan dan kekurangan utama dari gain informasi dan fungsi phi
Salah satu kelemahan utama dari gain informasi adalah bahwa fitur yang dipilih sebagai simpul berikutnya dalam pohon cenderung memiliki nilai unik yang lebih banyak. Keuntungan dari gain informasi adalah cenderung memilih fitur yang paling berdampak yang berada dekat dengan akar pohon. Ini adalah ukuran yang sangat baik untuk memutuskan relevansi beberapa fitur. Fungsi phi juga merupakan ukuran yang baik untuk memutuskan relevansi beberapa fitur berdasarkan "kebaikan". Ini adalah formula fungsi gain informasi. Rumus ini menyatakan bahwa gain informasi adalah fungsi dari entropi sebuah simpul pohon keputusan dikurangi entropi pemisahan kandidat di simpul t dari sebuah pohon keputusan.
Ini adalah rumus fungsi phi. Fungsi phi dimaksimalkan ketika fitur yang dipilih membagi sampel sedemikian rupa sehingga menghasilkan pemisahan yang homogen dan memiliki jumlah sampel yang kurang lebih sama di setiap pemisahan.
Kita akan menetapkan D, yang merupakan kedalaman pohon pilihan yang sedang kita bangun, menjadi tiga (D = 3). Kita juga memiliki kumpulan informasi yang diambil dari tes kanker dan non-kanker dan transformasi menyoroti bahwa tes tersebut memiliki atau tidak memiliki. Jika sebuah tes mencakup perubahan yang disertakan pada saat itu, maka tes tersebut positif terhadap perubahan tersebut, dan akan disebut sebagai tes. Jika suatu tes tidak memiliki perubahan include pada saat itu, maka tes tersebut negatif untuk perubahan tersebut, dan akan disebut dengan nol.
Evaluasi Pohon Keputusan (Decision Tree)
Penting untuk mengetahui pengukuran yang digunakan untuk mengevaluasi pohon keputusan. Metrik utama yang digunakan adalah akurasi, sensitivitas, spesifisitas, presisi, tingkat kesalahan prediksi negatif, tingkat kesalahan prediksi positif, dan tingkat pengabaian prediksi negatif. Semua pengukuran ini berasal dari jumlah positif benar, positif palsu, negatif benar, dan negatif palsu yang diperoleh saat menjalankan serangkaian sampel melalui model klasifikasi pohon keputusan. Selain itu, sebuah matriks kebingungan dapat dibuat untuk menampilkan hasil-hasil ini. Semua metrik utama ini memberikan informasi yang berbeda tentang kelebihan dan kelemahan model klasifikasi yang dibangun berdasarkan pohon keputusan Anda. Sebagai contoh, sensitivitas yang rendah dengan spesifisitas yang tinggi bisa menunjukkan bahwa model klasifikasi yang dibangun dari pohon keputusan tidak baik dalam mengidentifikasi sampel kanker dibandingkan dengan sampel non-kanker.
Disadur dari: en.wikipedia.org

